tips：本文为学习的过程中做的笔记和总结如有错误欢迎指正。通过不同的坐标系统展开，梳理，把坐标系统和渲染相关知识系统化。
    1.渲染管线
    含义：类似于流水线工作 上一个阶段的输出作为下个阶段的输入。
    应用阶段：

    1.   1. CPU上 计算场景中的基本数据。
    2.   1. 加速算法，粗粒度剔除。可见光裁剪 可见场景物体裁剪   
    3.   1. 设置渲染状态，准备渲染参数。
    4.   1. 输出渲染图元到显存。顶点数据，纹理贴图，MVP变换矩阵

    几何阶段：（下边会详细分析一下几何阶段）

    1.   1. GPU上执行
    2.   1. 顶点着色器
    3.   1. 曲面细分
    4.   1. 投影，把3d场景转换为2d场景
    5.   1. 裁剪
    6.   1. 屏幕映射

    光栅化阶段：

    1.   1. 三角形设置
    2.   1. 抗锯齿

    逐片元操作：

    1.   1. 片源着色器
    2.   1. 颜色混合
    3.   1. 目标缓冲区

    2.Object3D 基类（three.js）

    • 继承它的子类：Scene、Camera、Mesh、Light
    • 核心属性：matrix（本地矩阵） 、matrixWorld（世界矩阵）

    3.坐标系

    • 本地坐标系（局部坐标系）：原点为模型位于世界坐标的位置。其他顶点以这个点为原点计算坐标。
    • 世界坐标系：threejs中世界坐标单位为1 。这个1 没有实际的计量单位，如果想和物理世界里的计量单位关联可以等比进行计算。同时这个坐标长度也是无限的。（threejs是右手坐标系）

    • 屏幕坐标系：也是OpenGL中默认的屏幕坐标系，原点位于屏幕左下角。向上为Y轴正方向，向右为X轴正方向。将NDC坐标系转换到屏幕坐标系需要用到视口变换。视口变换矩阵定义了屏幕坐标与NDC坐标的对应关系，不同分辨率的屏幕会有不同的视口变换矩阵。

    • 浏览器坐标系（canvas坐标系）：原点位于左上角。X轴正方向和屏幕坐标系是相同的，Y轴正方向和屏幕坐标系相反。

    • 观察坐标系（相机坐标系）：通过Scene渲染的场景内容并不是展现全部内用给用户，而是通过Camera的视锥体信息得到的空间，这个空间是实际展现给用户，以相机为原点的坐标系，也叫相机坐标系。
    • 裁剪坐标系（投影坐标系）：基于观察坐标系进一步优化需要渲染的场景范围。根据相机设置的fov和近截面远截面，截面宽高比决定的。

    经过投影变换后坐标会多一个w分量（1，2，3，w）它用来描述一个点离观察点（观察坐标系的原点） 的距离所带来的影响

    • 规范化设备坐标系（NDC）

    规范化多设备坐标系统，设备多样性需要有一个统一的规范描述转换 为2D坐标后的点应该绘制在 屏幕 那个位置。从裁剪坐标系转换NDC坐标系需要用到透视除法，将xyz三个分量分别处以w分量。
    NDC坐标都在-1到1之间。坐标原点位于场景的中心。x y 方向左正 上正


    4.MVP矩阵
    作用：GPU渲染3D图形 需要把3D图形的顶点通过变换和投影转换成2D纹理坐标。这个转换的过程就是
    通过MVP矩阵左乘3D坐标的顶点得到的。

    • M矩阵

    含义：表示模型的旋转 平移 缩放
    模型顶点左乘M矩阵作用：将模型转换到世界坐标系下

    • V矩阵

    含义：表示相机的 旋转 平移 缩放。注意渲染管线中使用的V矩阵是 是相机世界矩阵的 逆矩阵，因为
    相机的旋转 缩放 平移 和 世界的是相反的。操作相机世界不动 和 操作世界相机不动。
    模型顶点左乘完M矩阵再乘V矩阵的作用：把模型从世界坐标转换为视图坐标系

    • P矩阵

    含义：P矩阵是根据相机的视锥体信息构建的。
    模型左乘M矩阵再乘V矩阵再乘P矩阵的效果：把模型从视觉坐标系转换到投影坐标系。
    5.相机投影

    • 投影：三维坐标下物的每个顶点， 投影到相同到平面上（通常在渲染阶段投影到屏幕上）。
    • 正交投影相机
    • 透视相机
      1. 进大远小
      2. 投影时射线之间不是平行的 ，是和近裁面和远裁面 顶点连线平行
      3. fov：是视锥体竖直方向上张角（角度）。人眼的fov一般为140度
      4. aspect：实际窗口的纵横比（一般为canvas的宽高比）
      5. near：近截面距离相机的距离
      6. far：远截面距离相机的距离
    • 立方相机
    • 立体相机

    6.几何阶段分析

    1. 顶点着色器-视图变换 ：参照第五点完成了从模型坐标转换到视图坐标。
    2. 曲面细分：根据算法在顶点之间进行插值，三角面变多，模型趋近于平滑。
    3. 几何着色器：操作对象为图元，基于一个给定到图元进行操作生成相关的图元。
    4. 投影：参照第五点完成了从视图坐标转换到投影坐标。
    5. 裁剪： 模型转换到NDC坐标系中后 如果顶点超过 [-1,1] 则超出了可视范围 会被裁剪。
    6. 屏幕映射：标准设备坐标系下的点映射到输出设备到屏幕坐标系中。两者存在转换关系。

    8.归一化（坐标转换）
    含义：通过上边几何阶段分析。知道了模型从世界坐标如何一步一步转换到屏幕坐标最终显示。
    这个过程中存在一个重要到坐标系统规范。NDC 设备标准坐标系。它建立了从虚拟世界到物理
    世界坐标转换的桥梁。所以如果从输出设备上（显示器屏幕）获得一个点，反向的也可以得到一
    个模型的世界坐标系。正反的转换过程中都需要经过NDC坐标 这个过程就是归一化。
    在推导公式之前需要先定义一些参数和概念：
    推导对应的屏幕映射坐标系 为浏览器坐标系。
    输出设备：高h 宽w
    渲染画布（canvas）：距离屏幕上方T 距离屏幕左边L 宽度cw 高度 ch
    浏览器屏幕坐标：A(x,y)
    NDC坐标系：B(a,b)

    推导第一步：找到世界坐标系原点位于浏览器坐标系中点坐标。
    cx = cw/2+L，
    cy = ch/2+T

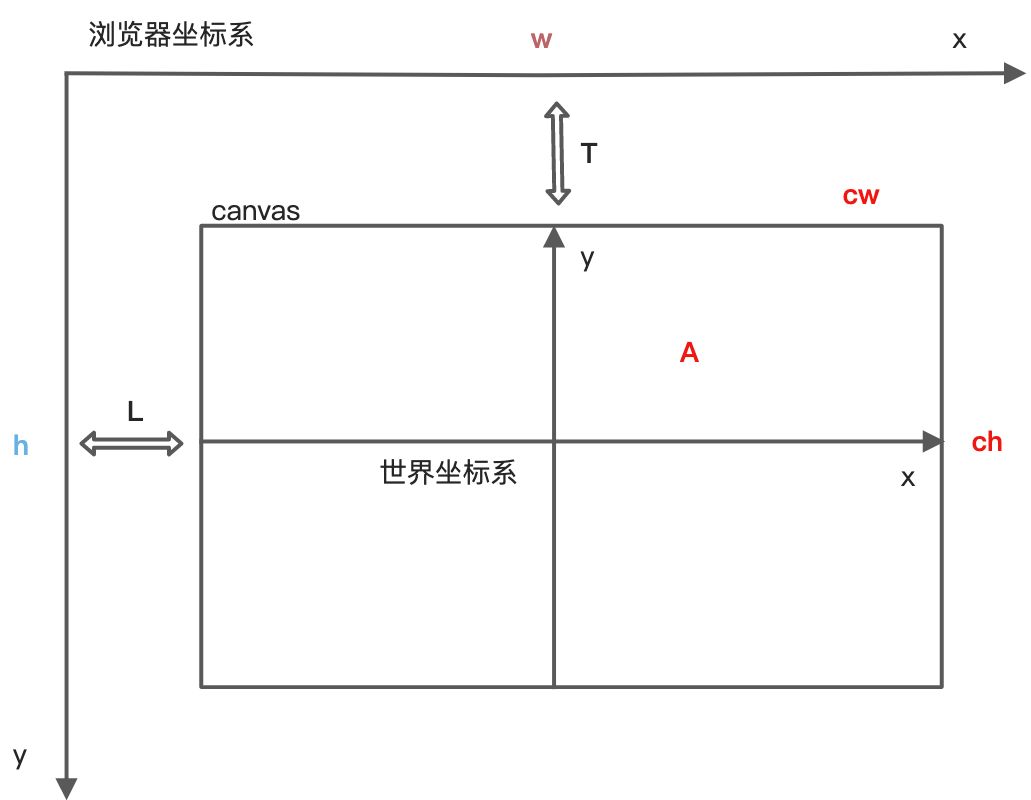
    webGL、three.js图形学基础详解 - 图1

    推导第二步：应用第一步坐标原点，推导 A坐标位于 世界坐标系中点位置A1(x1,y1)。注意这个位置单位是像素单位一般为px。至此浏览器坐标并未转换称为真正的世界坐标，而是把世界坐标单位和浏览器坐标单位看作是统一的，建立联系。
    x1 = x-cx
    y1 = cy-y(因为世界坐标和浏览器坐标y轴方向相反)

    推导第三步：把 A1的坐标 按照比例缩小到[-1,1]之间 ，除以 cw ch。
    注意：这里的处理原理，因为NDC坐标系是和世界坐标系等比一致的。
    x1/cx = (x-cx)/cw = (x+L)/cw-1/2
    y1/cy = (cy-y)/ch = (T-y)/ch+1/2

    至此把屏幕坐标带入 会得到一个归一化的坐标 。

    屏幕坐标转世界坐标：在threejs中 vector3 的方法unproject。可以将NDC的这个归一化坐标转换为世界坐 标。这个方法逆向推导MVP矩阵过程，得到世界坐标。

    世界坐标转屏幕坐标：思路还是首先需要得到一个标准化设备坐标，在three中 vector3 下的project方法根 据传入的相机经过MVP矩阵计算和透视分割算法得到了一个归一化坐标。这个归一化坐标 x1 y1。还是按照
    占比乘上转换为屏幕坐标单位的世界坐标。得出实际距离cx cy的距离 。因为屏幕坐标系是向左为正 向右为
    负。所以得到的距离原点的距离还需要加上一个半轴的距离和距离left 或 top的距离 最终是 x = x1*cw+cx

    x= (x1cw)/2+cw/2+L
    y = ch/2+T -(y1    ch)/2
    得出的结果可能和网上大部分转换给出的公式不同，这里是将canvas 未铺满的情况考虑 L T 为0 时 得到的公式与网上分析相同。

    9.Render图（转载）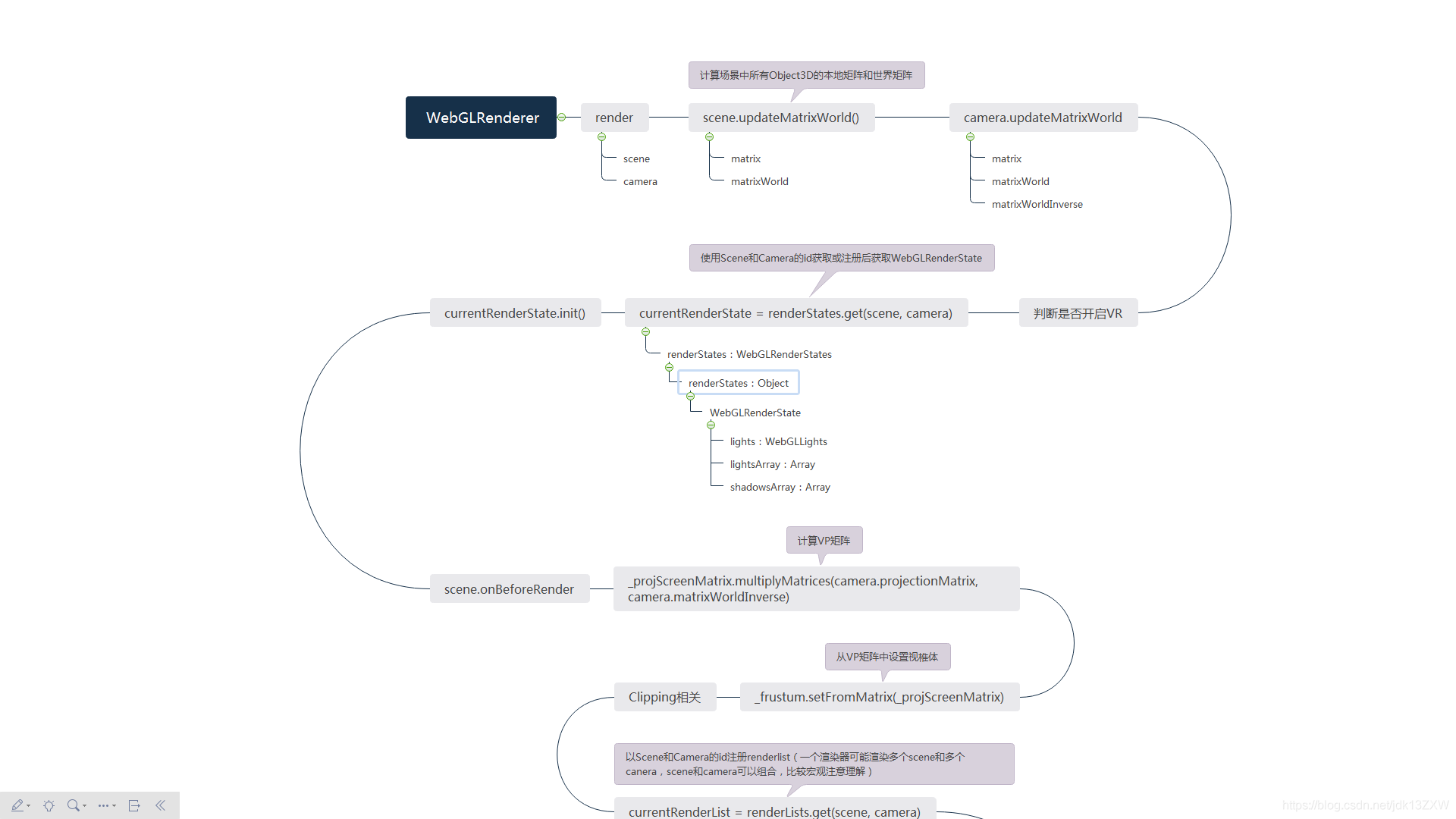
    image.png
    最后：下一篇要从几何数学入手 详细讲解 矩阵的运算 ，详细分析MPV。