一、向量
1.向量的定义
- 有大小和方向的线段。
- 向量描述的位移能被人为是与轴平行的位移序列。
- 三维向量 二纬向量
- 标量 只有大小没有方向的量。
- 零向量 表示没有位移。大小为零 没有方向。
2.标量与向量的计算
- 标量只能和向量乘除。
- 向量乘以标量效果是以标量的大小 缩小 放大 向量的长度。负数则向量的方向相反。
3.向量的模长
- |v| = √xx+yy 二维向量模
- |v|= √xx+yy+z*z 三维向量模
4.标准化向量
- 法线属于标准化向量
- 向量方向保持不变向量大小为1
- normV = v/|v| 向量除以它的模长
5.向量加减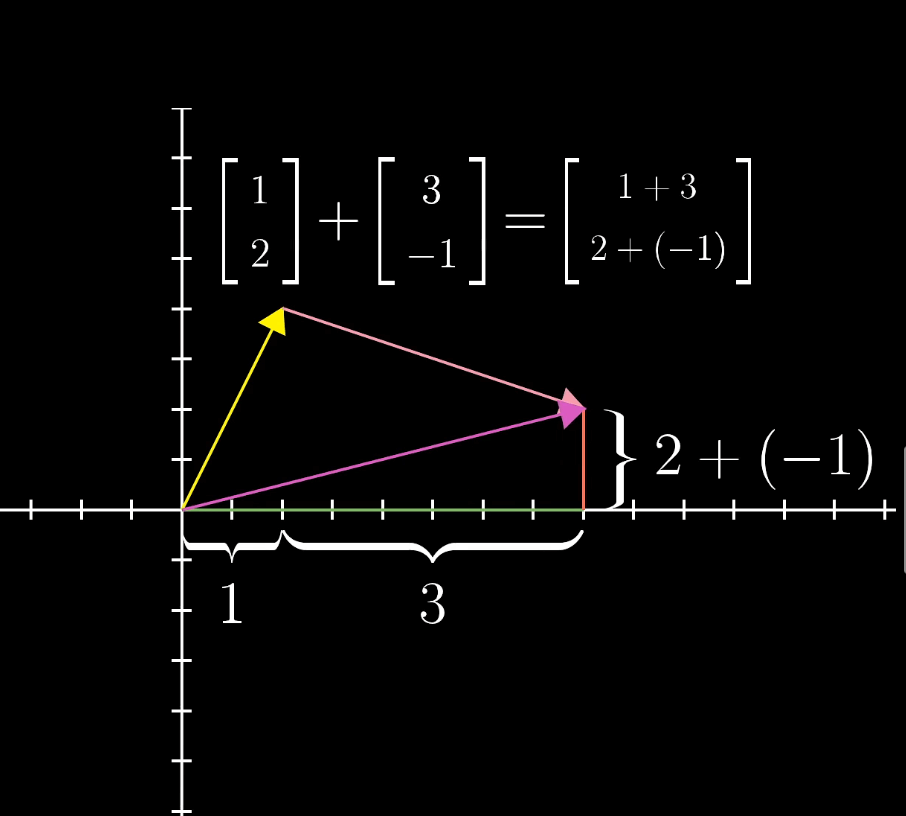
- 加法 :对应位置相加
- 减法:对应位置相减
- 相加的两个向量首位相连,最终粉色向量的尾部 是两个向量相加产生新的向量的尾部。黄色向量的起点为新向量的起点。这个过程可以看作是从起点开始沿黄色向量方向和大小运动一定距离,再沿棕色(我也不知道什么颜色)的向量方向运动向量的模长,最终到达终点。新的向量是沿直线从起点到终点运动。
向量相减可以看作运动过程,沿被减向量走到终点,执行减法,沿着减数向量的反方向走到起点。这样从被减数起点沿直线走到减数起点。得到新的向量。
6.向量的乘除向量积含义:a*b 向量b在向量a上的投影长度乘以向量a长度,也可以想像成向量b 通过 1x2 矩阵 b 线性转换的结果。
- 互相垂直的向量 乘积为0.
- 公式 (a,b)*(c,d) = ac+bd
7.向量差乘
- 含义:表示两个向量分别平移到另一个向量终点 所围成的面积。
- V x W = area; V在W右侧时候结果为正,在W左侧结果为负。
- 三维向量差乘:得出一个垂直与这两个向量组成平面的向量,这平面的法向量。向量的方向根据右手定则食指指向V 中指指向W 拇指指向 为这个新向量的方向。 向量大小为 两个向量组成平面面积。
- 公式: [v1 v2 v3] x [ w1 w2 w3 ] = [ v2w3-w2v3 v1w3-w1v3 v1w2-w1v2]
二、线性变换
- 原点位置不动网格线保持平行且等距分布
三、矩阵
1.矩阵向量积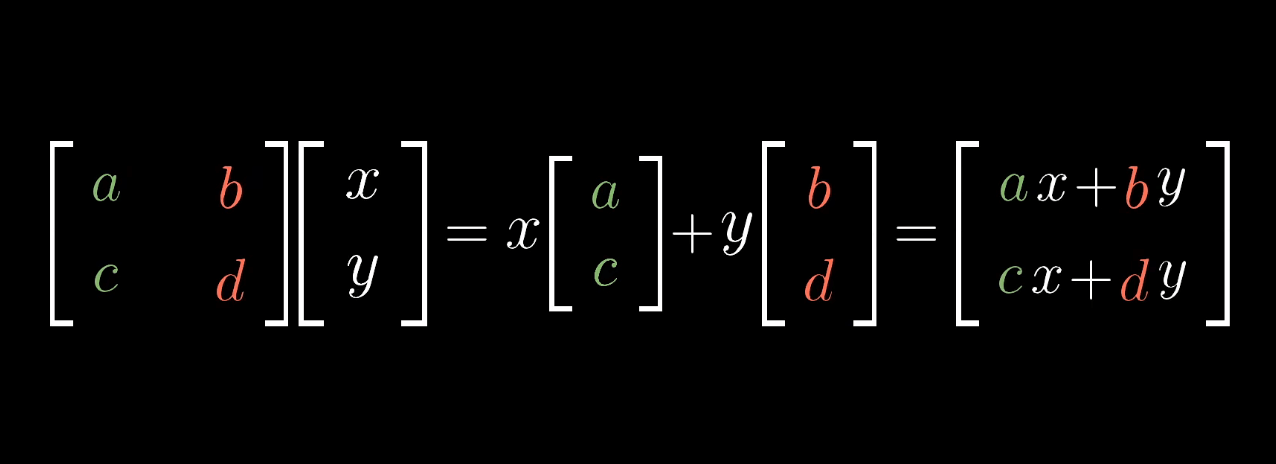
意义:空间上一个向量A(x,y) 。线性变换前的两个基向量 i(0,1) j(1,0)
变换后 i(1,-2) j(3,0)
线性变换后 想得到A1(x1,y1)向量 。求出变换后的基础向量组成矩阵。乘以原始A向量能得到新的A1向量。
2.矩阵乘法
- 矩阵乘法的实际意义: 描述一次线性变换(旋转,放大,缩小, 裁剪)变换过程从右向左读。
- 计算推导过程:右侧矩阵第一列向量经过左侧矩阵的线性变换得出一个新的向量,这个过程矩阵向量积,后边的n列同样经过左侧变换最后得出一个新的矩阵。
- 矩阵乘法符合结合律 (AB)C = A(BC) 根据乘法实际意义可以看出 在实际运动过程中都是从左到右取变换。
3.三维向量下的矩阵
三维矩阵下的基向量
1 1 1
0 1 0
-1 0 1三维下的矩阵乘法和二维矩阵乘法原理相同。
4.行列式
- 含义:线性变换矩阵基向量为边围成面积的大小经过线性变换后面积增加了n倍 那形容这次线性变换行列式为n。
比如以基向量为边构成的区域。在线性变换后,基向量发生变化,区域
面积也发生了变化。
- 定向空间改变:某个基向量相对于其他基向量的左右位置发生改变。这时候行列式的值为负数
二维行列式计算公式
a c<br />det = ad-bc 推导过程如下图,整块面积减去不想相关面积。 <br /> b d
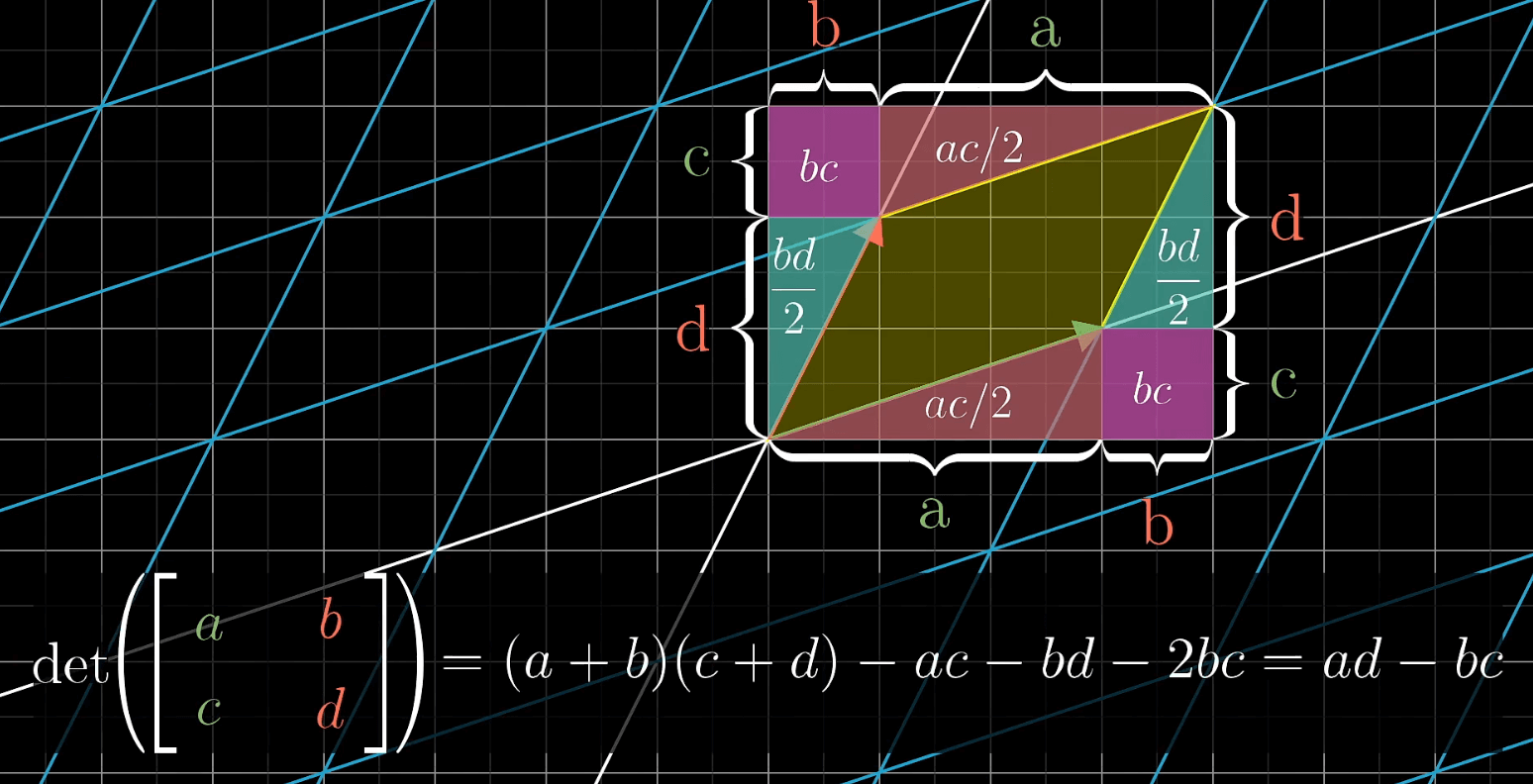
- 三维矩阵行列式计算
a b c e f d f d e
d e f = a det - b det + c det
g h i h i g i g h
这个推导目前不会
行列式值不为0时 才有逆矩阵。
5.逆矩阵
线性变换矩阵 乘 向量 得到的是一个变换后的向量。逆矩阵是通过 变换的 矩阵反推还原这个次变换的矩阵。所以 A-1*A 矩阵和逆矩阵相乘,相当 于没有发生线性变换。
计算公式:M-1= Madj/|M|
Madj 为M的伴随矩阵
|M|为矩阵的行列式
6.伴随矩阵
记忆方式:行列元素 排除本行本列的元素后生剩余四个元素求行列式。
a b c a c c11 c12 c13
d e f c22 = det c21 c22 c23
g h i g i c31 c32 c33
7.秩
线性变换 行列式为0时 转换为一维的 一条直线时 这个变换秩为1线性变换后空间为2维时 秩为2 。秩代表变换后的空间维数。

