最小二乘法

已知数据集：线性回归 - 图1

令：

线性回归 - 图2

最小二乘估计：找到最优的 线性回归 - 图3 使得 线性回归 - 图4%3DW%5ETx#card=math&code=f%28W%29%3DW%5ETx) 与 线性回归 - 图5 越接近越好，其中 线性回归 - 图6

目标函数（损失函数）为：线性回归 - 图7%3D%5Csum%7Bi%3D1%7D%5E%7BN%7D%5C%7CW%5ETx_i-y_i%5C%7C%5E2#card=math&code=L%28W%29%3D%5Csum%7Bi%3D1%7D%5E%7BN%7D%5C%7CW%5ETx_i-y_i%5C%7C%5E2)

参数估计的目标时最小化损失函数 线性回归 - 图8#card=math&code=L%28W%29) ：线性回归 - 图9#card=math&code=%5Chat%7BW%7D%3D%5Cmathop%7B%5Carg%5Cmin%7D_%7BW%7D%5C%20L%28W%29)

线性回归 - 图10 存在解析解：线性回归 - 图11%5E%7B-1%7DX%5ETY#card=math&code=W%3D%28X%5ETX%29%5E%7B-1%7DX%5ETY)

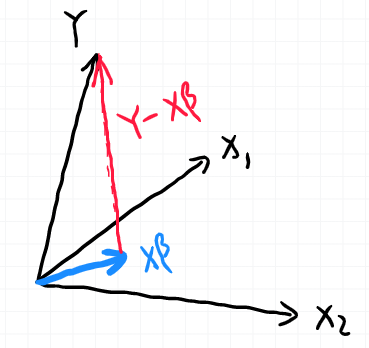
几何角度

将函数写作 线性回归 - 图12%3DW%5ETx%3Dx%5ET%5Cbeta#card=math&code=f%28W%29%3DW%5ETx%3Dx%5ET%5Cbeta) ，将 线性回归 - 图13 个样本看作 线性回归 - 图14 维空间，线性回归 - 图15 维的特征看作 线性回归 - 图16 维空间中的 线性回归 - 图17 维子空间。通俗的讲，将 线性回归 - 图18 看作 线性回归 - 图19 维的系数，在 线性回归 - 图20 维的子空间中采样 线性回归 - 图21 个点即是 线性回归 - 图22 。而 线性回归 - 图23 是不在这个子空间里的，则最小化 线性回归 - 图24#card=math&code=L%28%5Cbeta%29) 就是让红色的线最短，即让 线性回归 - 图25 向量与子空间的距离最近，则需要找到 线性回归 - 图26 相对于子空间的投影蓝色，这个投影是 线性回归 - 图27 的线性组合即 线性回归 - 图28 ， 线性回归 - 图29 向量与子空间的距离即 线性回归 - 图30 ，由于最优解的距离向量一定是垂直于子空间的，即垂直于 线性回归 - 图31 的每一列，有 线性回归 - 图32%3D0#card=math&code=X%5ET%28Y-X%5Cbeta%29%3D0) ，可得 线性回归 - 图33%5E%7B-1%7DX%5ETY#card=math&code=%5Cbeta%3D%28X%5ETX%29%5E%7B-1%7DX%5ETY)

线性回归 - 图34

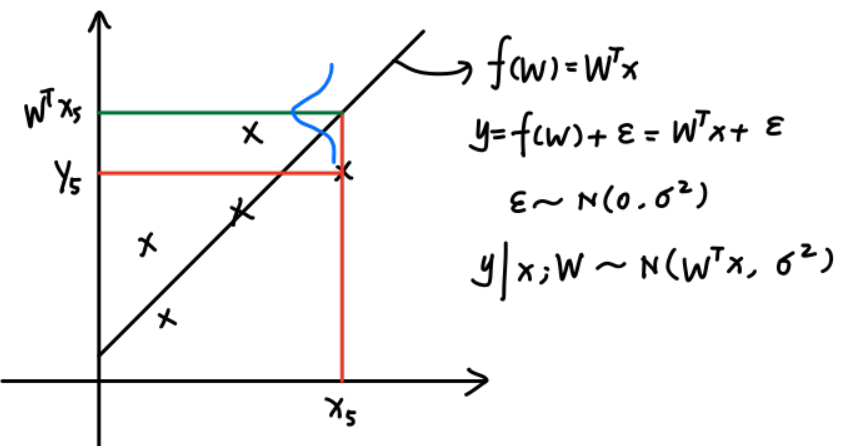
概率角度

假定真实数据和最优模型之间有一定的误差 线性回归 - 图35#card=math&code=%5Cepsilon%5Csim%20N%280%2C%5Csigma%5E2%29)

令 线性回归 - 图36%2B%5Cepsilon#card=math&code=y%3Df%28W%29%2B%5Cepsilon) , 其中 线性回归 - 图37%3DW%5ETx#card=math&code=f%28W%29%3DW%5ETx) ， 则 线性回归 - 图38#card=math&code=y%7Cx%3BW%5Csim%20N%28W%5ETx%2C%20%5Csigma%5E2%29)

概率密度函数为 线性回归 - 图39%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp%5C%7B-%5Cfrac%7B(y-W%5ETx)%5E2%7D%7B2%5Csigma%5E2%7D%5C%7D#card=math&code=p%28y%7Cx%3BW%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp%5C%7B-%5Cfrac%7B%28y-W%5ETx%29%5E2%7D%7B2%5Csigma%5E2%7D%5C%7D)

MLE:

似然函数：

线性回归 - 图40%20%26%20%3D%5Clog%20p(Y%7CX%3BW)%20%5C%5C%0A%09%26%20%3D%20%5Clog%20%5Cprod%7Bi%3D1%7D%5E%7BN%7Dp(y_i%7Cx_i%3BW)%20%5C%5C%0A%09%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Clog%20p(yi%7Cx_i%3BW)%20%5C%5C%0A%09%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Clog%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%20-%20%5Cfrac%7B1%7D%7B2%5Csigma%5E2%7D(yi-W%5ETx_i)%5E2%20%5C%5C%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%09%5Cmathcal%7BL%7D%28W%29%20%26%20%3D%5Clog%20p%28Y%7CX%3BW%29%20%5C%5C%0A%09%26%20%3D%20%5Clog%20%5Cprod%7Bi%3D1%7D%5E%7BN%7Dp%28yi%7Cx_i%3BW%29%20%5C%5C%0A%09%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Clog%20p%28yi%7Cx_i%3BW%29%20%5C%5C%0A%09%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Clog%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%20-%20%5Cfrac%7B1%7D%7B2%5Csigma%5E2%7D%28y_i-W%5ETx_i%29%5E2%20%5C%5C%0A%5Cend%7Bsplit%7D%0A)

最大化似然：

线性回归 - 图41%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20%5Csum%7Bi%3D1%7D%5E%7BN%7D-%5Cfrac%7B1%7D%7B2%5Csigma%5E2%7D(yi-W%5ETx_i)%5E2%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Csum%7Bi%3D1%7D%5E%7BN%7D(yi-W%5ETx_i)%5E2%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%09%5Chat%7BW%7D%20%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20%5Cmathcal%7BL%7D%28W%29%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20%5Csum%7Bi%3D1%7D%5E%7BN%7D-%5Cfrac%7B1%7D%7B2%5Csigma%5E2%7D%28yi-W%5ETx_i%29%5E2%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Csum_%7Bi%3D1%7D%5E%7BN%7D%28yi-W%5ETx_i%29%5E2%0A%5Cend%7Bsplit%7D%0A)

结论：LSE 线性回归 - 图42 MLE（噪声服从高斯分布的情况下）

正则化

对于样本数据 线性回归 - 图43 来说，它表示 线性回归 - 图44 个样本，每个样本为 线性回归 - 图45 的特征向量。如果 线性回归 - 图46 ，则样本数过少，线性回归 - 图47 不可逆，造成过拟合。

过拟合的处理方式：

  1. 加数据（线性回归 - 图48 足够大）
  2. 特征选择（特征提取）：降维（PCA）
  3. 正则化

正则化框架：

线性回归 - 图49%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5Cleft%5BL(W)%2B%5Clambda%20p(W)%5Cright%5D%0A#card=math&code=%5Chat%7BW%7D%3D%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20J%28W%29%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D_%7BW%7D%5C%20%5Cleft%5BL%28W%29%2B%5Clambda%20p%28W%29%5Cright%5D%0A)

L1正则化（Lasso）：线性回归 - 图50%3D%5C%7CW%5C%7C_1#card=math&code=p%28W%29%3D%5C%7CW%5C%7C_1)

L2正则化（Ridge/岭回归）：线性回归 - 图51%3D%5C%7CW%5C%7C_2%5E2%3DW%5ETW#card=math&code=p%28W%29%3D%5C%7CW%5C%7C_2%5E2%3DW%5ETW)

求解析解：

线性回归 - 图52%20%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%5C%7CW%5ETx_i-y_i%5C%7C%5E2%2B%5Clambda%20W%5ETW%20%5C%5C%0A%09%26%20%3D%20(W%5ETX%5ET-Y%5ET)(XW-Y)%2B%5Clambda%20W%5ETW%20%5C%5C%0A%09%26%20%3D%20W%5ETX%5ETXW-2W%5ETX%5ETY%2BY%5ETY%2B%5Clambda%20W%5ETW%20%20%5C%5C%0A%09%26%20%3D%20W%5ET(X%5ETX%2B%5Clambda%20I)W-2W%5ETX%5ETY%2BY%5ETY%20%5C%5C%0A%09%5Cfrac%7B%5Cpartial%7BJ(W)%7D%7D%7B%5Cpartial%7BW%7D%7D%20%26%20%3D%0A%092(X%5ETX-%5Clambda%20I)W-2X%5ETY%20%3D%200%20%5C%5C%0A%09%5Chat%7BW%7D%20%26%20%3D%20(X%5ETX%2B%5Clambda%20I)%5E%7B-1%7DX%5ETY%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%09J%28W%29%20%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%5C%7CW%5ETx_i-y_i%5C%7C%5E2%2B%5Clambda%20W%5ETW%20%5C%5C%0A%09%26%20%3D%20%28W%5ETX%5ET-Y%5ET%29%28XW-Y%29%2B%5Clambda%20W%5ETW%20%5C%5C%0A%09%26%20%3D%20W%5ETX%5ETXW-2W%5ETX%5ETY%2BY%5ETY%2B%5Clambda%20W%5ETW%20%20%5C%5C%0A%09%26%20%3D%20W%5ET%28X%5ETX%2B%5Clambda%20I%29W-2W%5ETX%5ETY%2BY%5ETY%20%5C%5C%0A%09%5Cfrac%7B%5Cpartial%7BJ%28W%29%7D%7D%7B%5Cpartial%7BW%7D%7D%20%26%20%3D%0A%092%28X%5ETX-%5Clambda%20I%29W-2X%5ETY%20%3D%200%20%5C%5C%0A%09%5Chat%7BW%7D%20%26%20%3D%20%28X%5ETX%2B%5Clambda%20I%29%5E%7B-1%7DX%5ETY%0A%5Cend%7Bsplit%7D%0A)

对于任意的 线性回归 - 图53 ，线性回归 - 图54 一定是半正定的，则 线性回归 - 图55 一定是正定的，所以 线性回归 - 图56 一定可逆。

正则化（贝叶斯角度）：

线性回归 - 图57

假设线性回归 - 图58先验为线性回归 - 图59#card=math&code=W%5Csim%20N%280%2C%5Csigma_0%5E2%29)

则

线性回归 - 图60%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp%5C%7B-%5Cfrac%7B(y-W%5ETx%5E2)%7D%7B2%5Csigma%5E2%7D%5C%7D%20%5C%5C%0Ap(W)%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma_0%7Dexp%5C%7B-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma_0%5E2%7D%5C%7D%0A#card=math&code=p%28y%7CW%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7Dexp%5C%7B-%5Cfrac%7B%28y-W%5ETx%5E2%29%7D%7B2%5Csigma%5E2%7D%5C%7D%20%5C%5C%0Ap%28W%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma_0%7Dexp%5C%7B-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma_0%5E2%7D%5C%7D%0A)

由贝叶斯定理得：

线性回归 - 图61%3D%5Cfrac%7Bp(y%7CW)p(W)%7D%7Bp(y)%7D%0A#card=math&code=p%28W%7Cy%29%3D%5Cfrac%7Bp%28y%7CW%29p%28W%29%7D%7Bp%28y%29%7D%0A)

其中，在数据已知得情况下，线性回归 - 图62#card=math&code=p%28y%29) 为常量，可忽略。

则

线性回归 - 图63p(W)%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma_0%7Dexp%5Cleft%5C%7B-%5Cfrac%7B(y-W%5ETx)%5E2%7D%7B2%5Csigma%5E2%7D-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma_0%5E2%7D%5Cright%5C%7D%0A#card=math&code=p%28y%7CW%29p%28W%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma_0%7Dexp%5Cleft%5C%7B-%5Cfrac%7B%28y-W%5ETx%29%5E2%7D%7B2%5Csigma%5E2%7D-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma_0%5E2%7D%5Cright%5C%7D%0A)

所以

线性回归 - 图64%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%20%5C%20%5C%20p(y%7CW)p(W)%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20log%5Cleft%5Bp(y%7CW)p(W)%5Cright%5D%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20log%5Cleft(%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma_0%7D%5Cright)-%5Cfrac%7B(y-W%5ETx)%5E2%7D%7B2%5Csigma%5E2%7D-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma_0%5E2%7D%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Cleft(%5Cfrac%7B(y-W%5ETx)%5E2%7D%7B2%5Csigma%5E2%7D-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma0%5E2%7D%5Cright)%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Cleft((y-W%5ETx)%5E2-%5Cfrac%7B%5Csigma%5E2%7D%7B%5Csigma0%5E2%7D%5C%7CW%5C%7C%5E2%5Cright)%20%5C%5C%0A%09%26%20%5CLeftrightarrow%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Csum%7Bi%3D1%7D%5EN%5C%7CW%5ETx_i-y_i%5C%7C%5E2%2B%5Clambda%20W%5ETW%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%09%5Chat%7BW%7D%20%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20%20p%28W%7Cy%29%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%20%5C%20%5C%20p%28y%7CW%29p%28W%29%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20log%5Cleft%5Bp%28y%7CW%29p%28W%29%5Cright%5D%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmax%7D%7BW%7D%5C%20%5C%20log%5Cleft%28%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma%7D%5Cfrac%7B1%7D%7B%5Csqrt%7B2%5Cpi%7D%5Csigma_0%7D%5Cright%29-%5Cfrac%7B%28y-W%5ETx%29%5E2%7D%7B2%5Csigma%5E2%7D-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma_0%5E2%7D%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Cleft%28%5Cfrac%7B%28y-W%5ETx%29%5E2%7D%7B2%5Csigma%5E2%7D-%5Cfrac%7B%5C%7CW%5C%7C%5E2%7D%7B2%5Csigma0%5E2%7D%5Cright%29%20%5C%5C%0A%09%26%20%3D%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Cleft%28%28y-W%5ETx%29%5E2-%5Cfrac%7B%5Csigma%5E2%7D%7B%5Csigma0%5E2%7D%5C%7CW%5C%7C%5E2%5Cright%29%20%5C%5C%0A%09%26%20%5CLeftrightarrow%20%5Cmathop%7B%5Carg%5Cmin%7D%7BW%7D%5C%20%5C%20%5Csum_%7Bi%3D1%7D%5EN%5C%7CW%5ETx_i-y_i%5C%7C%5E2%2B%5Clambda%20W%5ETW%0A%5Cend%7Bsplit%7D%0A)

即就是：

Regularized LSE 线性回归 - 图65 MAP (noise is Gaussian Distribution)