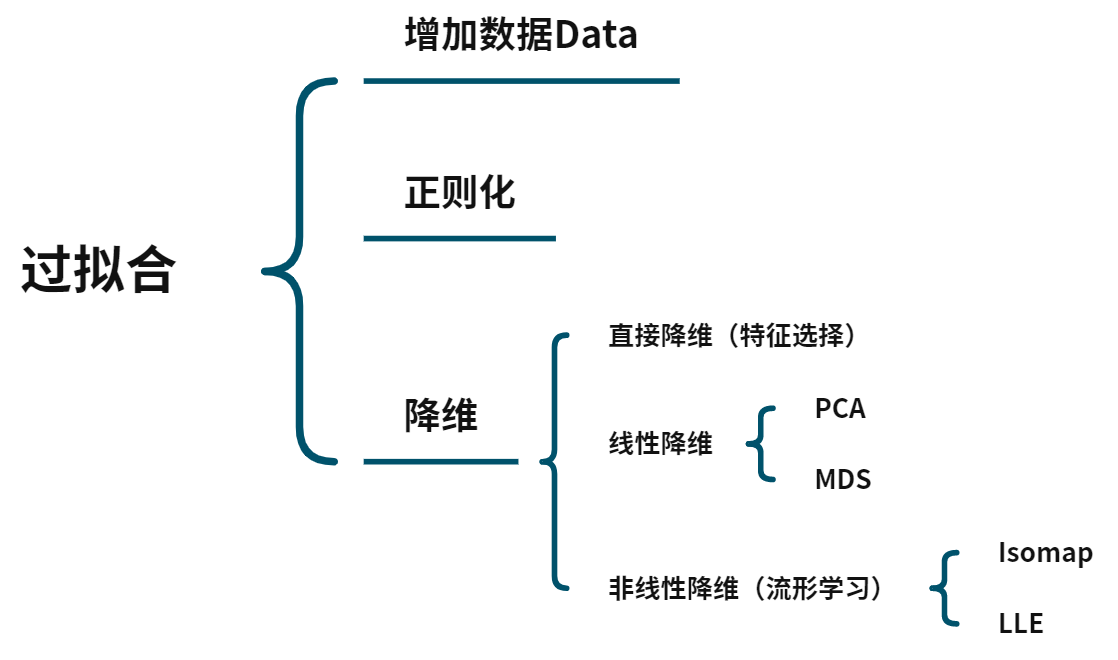
降维的原因

数据在高维空间中是极度稀疏的，数据量有限的情况下，直接用数据特征训练的模型容易过拟合。

维度灾难是由数据稀疏性导致的。

降维 - 图1

预备定义

Data：

降维 - 图2%7BN%20%5Ctimes%20p%7D%5E%7B%5Ctop%7D%20%3D%20%0A%5Cleft(%5Cbegin%7Barray%7D%7Bllll%7Dx%7B1%7D%5E%7B%5Ctop%7D%20%5C%5C%20x%7B2%7D%5E%7B%5Ctop%7D%20%5C%5C%20%5Cvdots%20%5C%5C%20x%7BN%7D%5E%7B%5Ctop%7D%5Cend%7Barray%7D%5Cright)%20%3D%20%0A%5Cleft(%5Cbegin%7Barray%7D%7Bllll%7D%0Ax%7B11%7D%20%26%20x%7B12%7D%20%26%20%5Ccdots%20%26%20x%7B1p%7D%20%5C%5C%0Ax%7B21%7D%20%26%20x%7B22%7D%20%26%20%5Ccdots%20%26%20x%7B2p%7D%20%5C%5C%0A%5Cvdots%20%26%20%5Cvdots%20%26%20%5Cddots%20%26%20%5Cvdots%20%5C%5C%0Ax%7BN1%7D%20%26%20x%7BN2%7D%20%26%20%5Ccdots%20%26%20x%7BNp%7D%20%5C%5C%0A%5Cend%7Barray%7D%5Cright)%0A#card=math&code=X%3D%5Cleft%28%5Cbegin%7Barray%7D%7Bllll%7Dx%7B1%7D%20%26%20x%7B2%7D%20%26%20%5Ccdots%20%26%20x%7BN%7D%5Cend%7Barray%7D%5Cright%29%7BN%20%5Ctimes%20p%7D%5E%7B%5Ctop%7D%20%3D%20%0A%5Cleft%28%5Cbegin%7Barray%7D%7Bllll%7Dx%7B1%7D%5E%7B%5Ctop%7D%20%5C%5C%20x%7B2%7D%5E%7B%5Ctop%7D%20%5C%5C%20%5Cvdots%20%5C%5C%20x%7BN%7D%5E%7B%5Ctop%7D%5Cend%7Barray%7D%5Cright%29%20%3D%20%0A%5Cleft%28%5Cbegin%7Barray%7D%7Bllll%7D%0Ax%7B11%7D%20%26%20x%7B12%7D%20%26%20%5Ccdots%20%26%20x%7B1p%7D%20%5C%5C%0Ax%7B21%7D%20%26%20x%7B22%7D%20%26%20%5Ccdots%20%26%20x%7B2p%7D%20%5C%5C%0A%5Cvdots%20%26%20%5Cvdots%20%26%20%5Cddots%20%26%20%5Cvdots%20%5C%5C%0Ax%7BN1%7D%20%26%20x%7BN2%7D%20%26%20%5Ccdots%20%26%20x_%7BNp%7D%20%5C%5C%0A%5Cend%7Barray%7D%5Cright%29%0A)

Sample Mean：降维 - 图3

Sample Covariance：降维 - 图4%5Cleft(x%7Bi%7D-%5Cbar%7Bx%7D%5Cright)%5E%7B%5Ctop%7D%20%3D%20%5Cfrac%7B1%7D%7BN%7DX%5E%7B%5Ctop%7DHH%5E%7B%5Ctop%7DX%3D%5Cfrac%7B1%7D%7BN%7DX%5E%7B%5Ctop%7DHX#card=math&code=S%7Bp%20%5Ctimes%20p%7D%3D%5Cfrac%7B1%7D%7BN%7D%20%5Csum%7Bi%3D1%7D%5E%7BN%7D%5Cleft%28x%7Bi%7D-%5Cbar%7Bx%7D%5Cright%29%5Cleft%28x_%7Bi%7D-%5Cbar%7Bx%7D%5Cright%29%5E%7B%5Ctop%7D%20%3D%20%5Cfrac%7B1%7D%7BN%7DX%5E%7B%5Ctop%7DHH%5E%7B%5Ctop%7DX%3D%5Cfrac%7B1%7D%7BN%7DX%5E%7B%5Ctop%7DHX)

其中：降维 - 图5#card=math&code=H%3D%28%5Cmathbf%7BI%7D_N-%5Cfrac%7B1%7D%7BN%7D%5Cmathbf%7B1%7D_N%5Cmathbf%7B1%7D_N%5E%7B%5Ctop%7D%29) 被称为中心矩阵，目的是对数据 降维 - 图6 做中心化，降维 - 图7

PCA（最大投影方差）

  • 一个中心：原始特征空间的重构
  • 两个基本点：
    • 最大投影方差
    • 最小重构距离

思路1：最大投影方差

  1. 数据特征的中心化： 降维 - 图8
  2. 选择投影方向： 降维 - 图9%5E%7B%5Ctop%7Du%2C%5C%7Cu%5C%7C%3D1#card=math&code=%28x_i-%5Cbar%7Bx%7D%29%5E%7B%5Ctop%7Du%2C%5C%7Cu%5C%7C%3D1)
  3. 最大化投影后的方差：

降维 - 图10u%20%5Cright)%5E2%20%5C%5C%0A%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20u%5E%7B%5Ctop%7D(x_i-%5Cbar%7Bx%7D)(x_i-%5Cbar%7Bx%7D)%5E%7B%5Ctop%7Du%20%5C%5C%0A%26%20%3D%20u%5E%7B%5Ctop%7D%5Cleft(%5Csum%7Bi%3D1%7D%5EN%20(xi-%5Cbar%7Bx%7D)(x_i-%5Cbar%7Bx%7D)%5E%7B%5Ctop%7D%20%5Cright)u%20%5C%5C%0A%26%20%3D%20u%5E%7B%5Ctop%7D%5Ccdot%20NS%20%5Ccdot%20u%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0AJ%20%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%5Cleft%28%28xi-%5Cbar%7Bx%7D%5E%7B%5Ctop%7D%29u%20%5Cright%29%5E2%20%5C%5C%0A%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20u%5E%7B%5Ctop%7D%28xi-%5Cbar%7Bx%7D%29%28x_i-%5Cbar%7Bx%7D%29%5E%7B%5Ctop%7Du%20%5C%5C%0A%26%20%3D%20u%5E%7B%5Ctop%7D%5Cleft%28%5Csum%7Bi%3D1%7D%5EN%20%28x_i-%5Cbar%7Bx%7D%29%28x_i-%5Cbar%7Bx%7D%29%5E%7B%5Ctop%7D%20%5Cright%29u%20%5C%5C%0A%26%20%3D%20u%5E%7B%5Ctop%7D%5Ccdot%20NS%20%5Ccdot%20u%0A%5Cend%7Bsplit%7D%0A)

  1. 则优化问题变为：

降维 - 图11

可用拉格朗日法求解：

降维 - 图12%20%26%20%3D%20u%7B1%7D%5E%7B%5Ctop%7D%20S%20u%7B1%7D%2B%5Clambda%5Cleft(1-u%7B1%7D%5E%7B%5Ctop%7D%20u%5Cright)%20%5C%5C%20%0A%5Cfrac%7B%5Cpartial%20%5Calpha%7D%7B%5Cpartial%20u%7B1%7D%7D%20%26%20%3D%202%20S%20%5Ccdot%20u%7B1%7D-%5Clambda%20%5Ccdot%202%20u%7B1%7D%3D0%20%5C%5C%20%0AS%20u%7B1%7D%20%26%20%3D%20%5Clambda%20u%7B1%7D%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%5Cmathcal%7BL%7D%5Cleft%28u%7B1%7D%2C%20%5Clambda%5Cright%29%20%26%20%3D%20u%7B1%7D%5E%7B%5Ctop%7D%20S%20u%7B1%7D%2B%5Clambda%5Cleft%281-u%7B1%7D%5E%7B%5Ctop%7D%20u%5Cright%29%20%5C%5C%20%0A%5Cfrac%7B%5Cpartial%20%5Calpha%7D%7B%5Cpartial%20u%7B1%7D%7D%20%26%20%3D%202%20S%20%5Ccdot%20u%7B1%7D-%5Clambda%20%5Ccdot%202%20u%7B1%7D%3D0%20%5C%5C%20%0AS%20u%7B1%7D%20%26%20%3D%20%5Clambda%20u_%7B1%7D%0A%5Cend%7Bsplit%7D%0A)

得到 降维 - 图13 即是矩阵 降维 - 图14 的特征值，降维 - 图15 为 降维 - 图16 的特征向量。

思路2：最小重构距离（代价）

可以理解，PCA实际上是对原始特征空间的重构（平移和旋转），如图所示，假设 降维 - 图17 已经进行了中心化 降维 - 图18 ，同时重构的坐标轴为 降维 - 图19 。

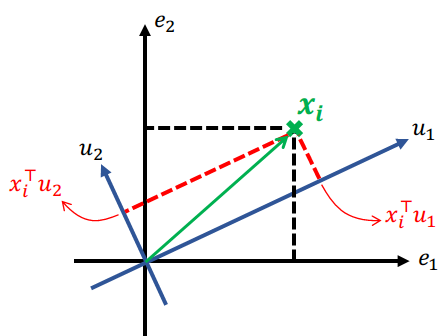
降维 - 图20

那么 降维 - 图21 在重构的坐标系下的坐标为 降维 - 图22#card=math&code=%28xi%5E%7B%5Ctop%7Du_1%2Cx_i%5E%7B%5Ctop%7Du_2%29) ，即对于 降维 - 图23 维的特征空间，原样本点可以表示为 ![](https://g.yuque.com/gr/latex?x_i%20%3D%20%5Csum%7Bk%3D1%7D%5Ep(xi%5E%7B%5Ctop%7Du_k)%5Ccdot%20u_k#card=math&code=x_i%20%3D%20%5Csum%7Bk%3D1%7D%5Ep%28xi%5E%7B%5Ctop%7Du_k%29%5Ccdot%20u_k) ，假设降维后的 ![](https://g.yuque.com/gr/latex?%5Chat%7Bx%7D_i%3D%5Csum%7Bk%3D1%7D%5Eq((xi%5E%7B%5Ctop%7Du_k)%5Ccdot%20u_k)%2Cq%3Cp#card=math&code=%5Chat%7Bx%7D_i%3D%5Csum%7Bk%3D1%7D%5Eq%28%28x_i%5E%7B%5Ctop%7Du_k%29%5Ccdot%20u_k%29%2Cq%3Cp) ，则可以定义重构误差为：

降维 - 图24%5Ccdot%20uk%20%5Cright%5C%7C%5E2%20%5C%5C%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%20J%20%26%20%3D%5Csum%7Bi%3D1%7D%5EN%20%5C%7Cxi-%5Chat%7Bx%7D_i%5C%7C%5E2%20%5C%5C%0A%20%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Cleft%5C%7C%20%5Csum_%7Bk%3Dq%2B1%7D%5Ep%20%28x_i%5E%7B%5Ctop%7Du_k%29%5Ccdot%20u_k%20%5Cright%5C%7C%5E2%20%5C%5C%0A%5Cend%7Bsplit%7D%0A)

这里注意：降维 - 图25%5Ccdot%20uk#card=math&code=%5Csum%7Bk%3Dq%2B1%7D%5Ep%20%28x_i%5E%7B%5Ctop%7Du_k%29%5Ccdot%20u_k) 实际上是一个向量，降维 - 图26 是向量的正交基，降维 - 图27#card=math&code=%28x_i%5E%7B%5Ctop%7Du_k%29) 是基上的坐标，则这个向量的二范数的平方（长度的平方）应该就等于坐标的内积（平方和）。所以有：

降维 - 图28%5E2%20%5C%5C%0A%20%26%20%5Ctriangleq%20%5Csum%7Bi%3D1%7D%5EN%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20%5Cleft(%20(xi-%5Cbar%7Bx%7D)%5E%7B%5Ctop%7Du_k%20%5Cright)%5E2%20%5C%5C%0A%20%26%20%5Ctriangleq%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20%5Csum%7Bi%3D1%7D%5EN%20%5Cfrac%7B1%7D%7BN%7D%20%5Cleft(%20(x_i-%5Cbar%7Bx%7D)%5E%7B%5Ctop%7Du_k%20%5Cright)%5E2%20%5C%5C%0A%20%26%20%3D%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20uk%5E%7B%5Ctop%7D%5Ccdot%20S%20%5Ccdot%20u_k%20%5C%5C%0A%20%26%20s.t.%20%5C%20%5C%20u_k%5E%7B%5Ctop%7Du_k%3D1%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%20J%20%26%20%3D%20%5Csum%7Bi%3D1%7D%5EN%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20%28x_i%5E%7B%5Ctop%7Du_k%29%5E2%20%5C%5C%0A%20%26%20%5Ctriangleq%20%5Csum%7Bi%3D1%7D%5EN%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20%5Cleft%28%20%28x_i-%5Cbar%7Bx%7D%29%5E%7B%5Ctop%7Du_k%20%5Cright%29%5E2%20%5C%5C%0A%20%26%20%5Ctriangleq%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20%5Csum%7Bi%3D1%7D%5EN%20%5Cfrac%7B1%7D%7BN%7D%20%5Cleft%28%20%28x_i-%5Cbar%7Bx%7D%29%5E%7B%5Ctop%7Du_k%20%5Cright%29%5E2%20%5C%5C%0A%20%26%20%3D%20%5Csum%7Bk%3Dq%2B1%7D%5Ep%20u_k%5E%7B%5Ctop%7D%5Ccdot%20S%20%5Ccdot%20u_k%20%5C%5C%0A%20%26%20s.t.%20%5C%20%5C%20u_k%5E%7B%5Ctop%7Du_k%3D1%0A%5Cend%7Bsplit%7D%0A)

则最小化重构代价的优化问题表示为：

降维 - 图29

我们知道 降维 - 图30 之间是相互独立（正交）的，所以这个求和的优化问题可以单独对每个分量进行优化，对单个分量进行优化时容易得出最佳的 降维 - 图31 即为 降维 - 图32 的最小特征值 降维 - 图33 对应的特征向量。即 降维 - 图34

SVD角度看PCA和PCoA

补充奇异值分解（Singular Value Decomposition）：

SVD是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设矩阵 降维 - 图35 是一个 降维 - 图36 的矩阵，定义矩阵 降维 - 图37 的SVD为：

降维 - 图38

其中 降维 - 图39 是一个是一个 降维 - 图40 的矩阵， 降维 - 图41 是一个 降维 - 图42 的矩阵，除了主对角线上的元素以外全为 降维 - 图43 ，主对角线上的每个元素都称为奇异值， 降维 - 图44 是一个 降维 - 图45 的矩阵。 降维 - 图46 和 降维 - 图47 都是酉矩阵，即满足 降维 - 图48 .

如何计算 降维 - 图49 呢？

将 降维 - 图50 和 降维 - 图51 做乘法，得到 降维 - 图52 的方阵，对其进行特征值分解：

降维 - 图53v_i%3D%5Clambda_iv_i%0A#card=math&code=%28A%5E%7B%5Ctop%7DA%29v_i%3D%5Clambda_iv_i%0A)

降维 - 图54 的所有特征向量张成一个 降维 - 图55 的矩阵 降维 - 图56 ，它被称为 降维 - 图57 的右奇异向量。

将 降维 - 图58 和 降维 - 图59 做乘法，得到 降维 - 图60 的方阵，对其进行特征值分解：

降维 - 图61u_i%3D%5Clambda_iu_i%0A#card=math&code=%28AA%5E%7B%5Ctop%7D%29u_i%3D%5Clambda_iu_i%0A)

降维 - 图62 的所有特征向量张成一个 降维 - 图63 的矩阵 降维 - 图64 ，它被称为 降维 - 图65 的左奇异向量。

由于 降维 - 图66 除了对角线上是奇异值其他位置都是 降维 - 图67 ，那我们只需要求出每个奇异值 降维 - 图68就可以了。

降维 - 图69

根据观察，特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

降维 - 图70

这样也就是说，我们可以不用 降维 - 图71 来计算奇异值，也可以通过求出 降维 - 图72 的特征值取平方根来求奇异值。

根据前两节的分析，可以知道进行PCA降维的前提是计算协方差矩阵 降维 - 图73 的特征值分解，从而选择出Principle Component Direction。从奇异值分解的角度，我们可以把 降维 - 图74 看作 降维 - 图75 ，即把 降维 - 图76 的特征值分解过程看作是 降维 - 图77 的奇异值分解过程。

定义 降维 - 图78 的奇异值分解为：

降维 - 图79%20%5Cend%7Barray%7D%5Cright.%0A#card=math&code=HX%3DU%5CSigma%20V%5E%7B%5Ctop%7D%20%5Crightarrow%20SVD%3A%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Blll%7D%20U%5E%7B%5Ctop%7DU%3DI%20%5C%5C%0AV%5E%7B%5Ctop%7DV%3DI%20%5C%5C%20%5CSigma%3Ddiag%28%5Csigma_i%29%20%5Cend%7Barray%7D%5Cright.%0A)

则：

降维 - 图80

降维 - 图81 和 降维 - 图82 有相同的eigenvalue

降维 - 图83 ：特征分解→得到方向（主成分），然后 降维 - 图84 得到坐标

降维 - 图85 ：特征分解→直接得到坐标（主坐标分析Principle Coordinate Analysis，PCoA）

概率角度看PCA（p-PCA）

对原数据 降维 - 图86 ，降维后的数据为 降维 - 图87。降维通过一个矩阵变换（投影）进行：

降维 - 图88

已知 降维 - 图89 分布，可求 降维 - 图90 分布，在已知数据 降维 - 图91 的情况下，可以计算后验 降维 - 图92 进行推断（降维）。

所以p-PCA主要包括两个部分：Learning→降维 - 图93 （EM算法）；Inference→降维 - 图94#card=math&code=p%28z%7Cx%29)

生成模型的思路如图：

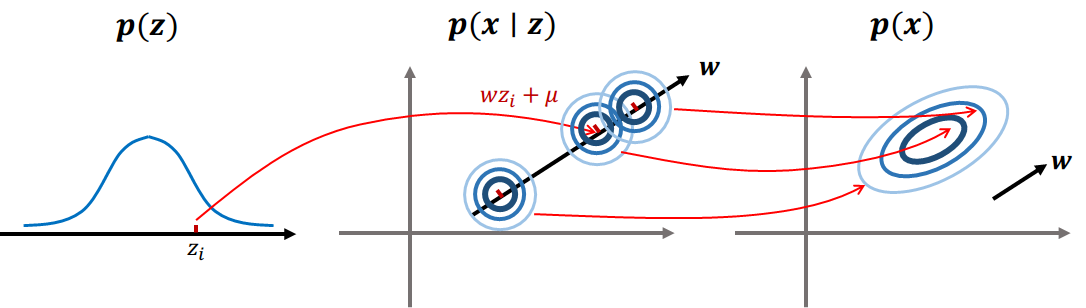
降维 - 图95

这里主要介绍 Inference：

根据已知的分布可以计算 降维 - 图96 的分布：

降维 - 图97

可以计算 降维 - 图98 的分布：

降维 - 图99

要计算 降维 - 图100 ，首先要求出组合的分布：

降维 - 图101

其中 降维 - 图102 为 降维 - 图103 的协方差：

降维 - 图104

所以有：

降维 - 图105

然后根据高斯分布这节的条件概率公式，计算得出 降维 - 图106 ：

降维 - 图107

降维 - 图108%0A#card=math&code=xb%7Cx_a%20%5Csim%20N%28%5Cmu%7Bb%20%5Ccdot%20a%7D%20%2B%20%5CSigma%7Bba%7D%5CSigma%7Baa%7D%5E%7B-1%7Dxa%2C%20%5CSigma%7Bbb%20%5Ccdot%20a%7D%29%0A)