一、题干： 网格照明

在大小为 n x n 的网格 grid 上，每个单元格都有一盏灯，最初灯都处于 关闭 状态。
给你一个由灯的位置组成的二维数组 lamps ，其中 lamps[i] = [rowi, coli] 表示 打开 位于 grid[rowi][coli] 的灯。即便同一盏灯可能在 lamps 中多次列出，不会影响这盏灯处于 打开 状态。
当一盏灯处于打开状态，它将会照亮 自身所在单元格 以及同一 行 、同一 列 和两条 对角线 上的 所有其他单元格 。
另给你一个二维数组 queries ，其中 queries[j] = [rowj, colj] 。对于第 j 个查询，如果单元格 [rowj, colj] 是被照亮的，则查询结果为 1 ，否则为 0 。在第 j 次查询之后 [按照查询的顺序] ，关闭 位于单元格 grid[rowj][colj] 上及相邻 8 个方向上（与单元格 grid[rowi][coli] 共享角或边）的任何灯。
返回一个整数数组 ans 作为答案， ans[j] 应等于第 j 次查询 queries[j] 的结果，1 表示照亮，0 表示未照亮。

示例 1：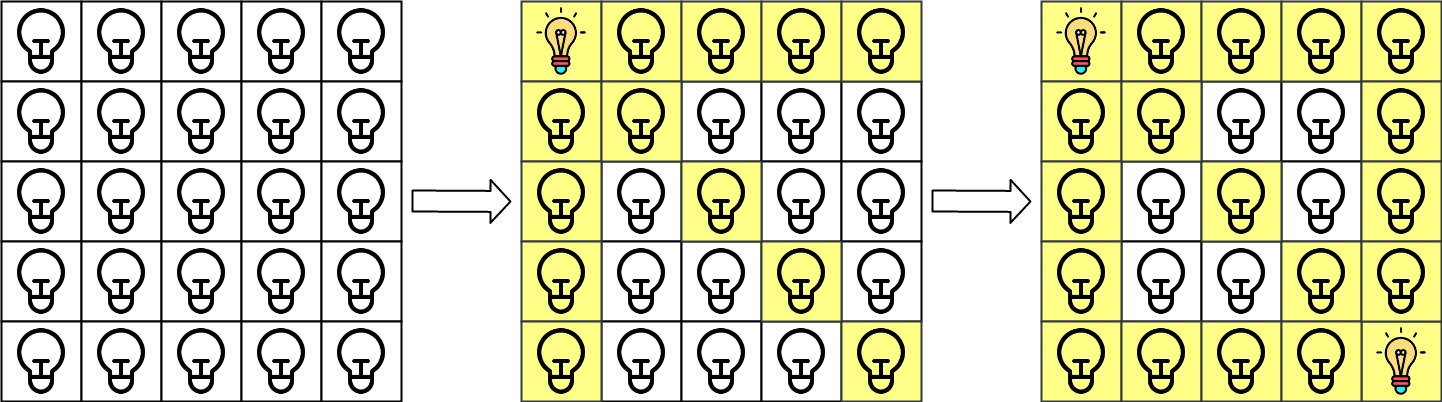

输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]] 输出：[1,0] 解释：最初所有灯都是关闭的。在执行查询之前，打开位于 [0, 0] 和 [4, 4] 的灯。第 0 次查询检查 grid[1][1] 是否被照亮（蓝色方框）。该单元格被照亮，所以 ans[0] = 1 。然后，关闭红色方框中的所有灯。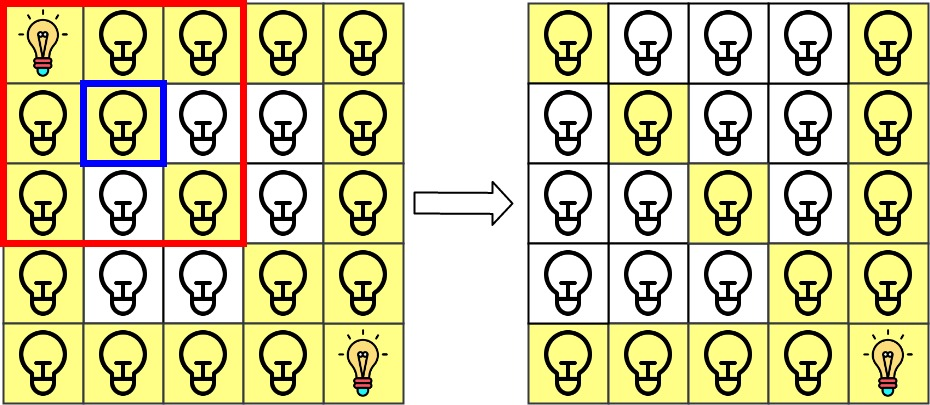

第 1 次查询检查 grid[1][0] 是否被照亮（蓝色方框）。该单元格没有被照亮，所以 ans[1] = 0 。然后，关闭红色矩形中的所有灯。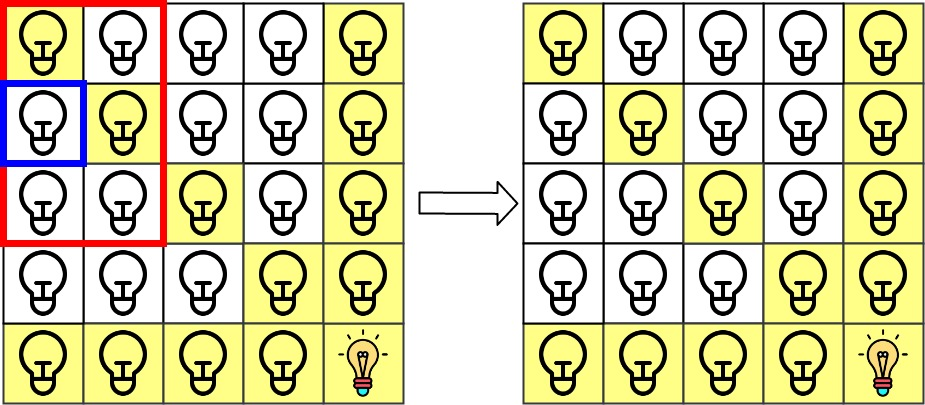

示例 2：
输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]] 输出：[1,1]
示例 3：
输入：n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]] 输出：[1,1,0]

提示：

• 1 <= n <= 109
• 0 <= lamps.length <= 20000
• 0 <= queries.length <= 20000
• lamps[i].length == 2
• 0 <= rowi, coli < n
• queries[j].length == 2
• 0 <= rowj, colj < n

二、解题思路：

1、初版：

第一反应：暴力求解，但是如果将整个网格数组模拟出来，显然超内存，如下所示：

func gridIllumination(n int, lamps [][]int, queries [][]int) []int {
    var arr [10e9][10e9]int//超内存
    var res []int
    var x1 int
    var y1 int
    //turn on，若是灯，则+1，若是被照亮，则+2
    for i:=0;i<len(lamps);i++ {
        x:=lamps[i][0]
        y:=lamps[i][1]
        if arr[x][y]&1==0{//偶数：no lamp
            arr[x][y]+=1
            for a:=0;a<n;a++{
                arr[x][a]+=2
                arr[a][y]+=2
            }
            for x1,y1=x-1,y-1;x1>=0&&y1>=0;x1,y1=x1-1,y1-1{
                arr[x1][y1]+=2
            }
            for x1,y1=x+1,y+1;x1<n&&y1<n;x1,y1=x1+1,y1+1{
                arr[x1][y1]+=2
            }
            for x1,y1=x+1,y-1;x1<n&&y1>=0;x1,y1=x1+1,y1-1{
                arr[x1][y1]+=2
            }
            for x1,y1=x-1,y+1;x1>=0&&y1<n;x1,y1=x1-1,y1+1{
                arr[x1][y1]+=2
            }
        }
    }
    //query
    for i:=0;i<len(queries);i++ {
        x:=queries[i][0]
        y:=queries[i][1]
        if arr[x][y]>0 {
            res=append(res,1)
            for x1,y1,ii:=x-1,y-1,1;ii<9;x1,y1,ii=x-1+ii/3,y-1+ii%3,ii+1{
                if x1<0||y1<0||x1>=n||y1>=n{
                    continue
                }
                if arr[x1][y1]&1==1{//奇数
                    //turn off
                    arr[x1][y1]-=1
                    for a:=0;a<n;a++{
                        arr[x][a]+=2
                        arr[a][y]+=2
                    }
                    for x1,y1=x-1,y-1;x1>=0&&y1>=0;x1,y1=x1-1,y1-1{
                        arr[x1][y1]+=2
                    }
                    for x1,y1=x+1,y+1;x1<n&&y1<n;x1,y1=x1+1,y1+1{
                        arr[x1][y1]+=2
                    }
                    for x1,y1=x+1,y-1;x1<n&&y1>=0;x1,y1=x1+1,y1-1{
                        arr[x1][y1]+=2
                    }
                    for x1,y1=x-1,y+1;x1>=0&&y1<n;x1,y1=x1-1,y1+1{
                        arr[x1][y1]+=2
                    }
                }
            }
        }else{
            res=append(res,0)
        }
    }
    return res
}

2、改进：

实际上，只需要记录对应的行，列和正反对角线上的灯数即可。

1. 需求1：满足queries查找，
   解决方案：使用四个map分别记录四个不同方向上的灯数，验证queries[j]是否被四个方向中的任意一个方向照亮。
2. 需求2：实现关闭九宫格内的灯，

解决方案：使用一个map记录所有坐标上的灯，如何通过坐标(x,y)唯一标识每个灯？使用n*x+y作为key来唯一标识每个灯。

因为0<=x,y<n，且x,y都是整数，n*x+y的值没有重复的，可证如下： 假设在范围内存在两个不同的点(x1,y1)和(x2,y2)，使得相等， 则：，即， 但是因为都是[0,n-1]范围内的整数，所以的范围都是[-(n-1),(n-1)]，故不可能等于n， 即不成立， 综上所述，得证。

const(
    ON,OFF=1,-1
)
func gridIllumination(n int, lamps [][]int, queries [][]int) []int {
    var row=make(map[int]int)
    var col=make(map[int]int)
    var diagonal=make(map[int]int)
    var antidiagonal=make(map[int]int)
    var isLamp=make(map[int]bool)
    turn:=func(x,y,flag int){
        row[x]+=flag
        col[y]+=flag
        diagonal[y-x]+=flag
        antidiagonal[y+x]+=flag
    }
    for _,lamp:=range lamps{
        x,y:=lamp[0],lamp[1]
        if !isLamp[x*n+y]{
            isLamp[x*n+y]=true
            turn(x,y,ON)
        }
    }
    var res =make([]int,len(queries))
    for i,q:=range queries{
        x,y :=q[0],q[1]
        if row[x]>0||col[y]>0||diagonal[y-x]>0||antidiagonal[y+x]>0{
            res[i]=1
        }
        //遍历九宫格
        for x1,y1,j:=x-1,y-1,1;j<9;x1,y1,j=x-1+j/3,y-1+j%3,j+1{
            if x1<0||y1<0||x1>=n||y1>=n{
                continue
            }
            if isLamp[x1*n+y1]{
                isLamp[x1*n+y1]=false
                turn(x1,y1,OFF)
            }
        }
    }
    return res
}