[C9][DP] 动态规划

• 用于在给定约束条件下优化某种指标
• 问题可分解为离散子问题
• 每种动态规划解决方案都涉及网络
• 单元格中的值通常是待优化的值
• 每个单元格都是一个子问题，你需要考虑如何将问题分解为子问题

  9.1 背包问题

  4磅背包偷物品，当前有3个物品：4磅3000$音响，3磅2k电脑，1磅1.5k吉他

简单算法

• 穷举所有可能的集合，获取可容纳的价值最高的集合。当物品数量上升，集合数量2^n
• 近似贪婪算法，非最优解

动态规划

• 按层遍历每种商品，每层可选包括这层与之前的商品
• 对于每种商品遍历每单位增加重量时，当前最大价值的商品组合

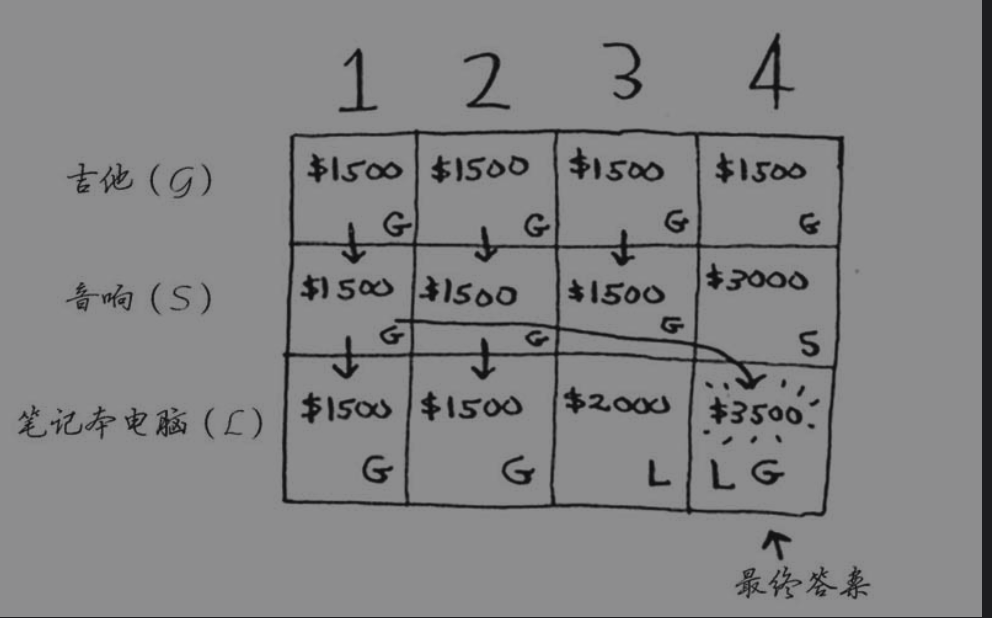
对于每个单元格都有：

• cell[i][j] = max(cell[i-1][j], 当前商品价值+cell[i-1][j-当前商品重量])
• 其中i表示行，即当前遍历物品
• j表示列，即递增重量序列

9.2 背包问题FAQ (A frequently asked questions)

Q1. 加入第四件商品-iphone，是否需要重新执行前面计算？

• 不需要，动态规划逐步计算最大价值

Q2. 每一列随着物品增加最大价值会减小吗？

• 不会，因为每次计算max时都会加入上一个cell中的值

Q3. 行的排列顺序发生变化时结果如何？

• 不影响

Q4. 可以逐列而不是逐行填充网络吗？

• 对某些问题，可能有影响

Q5. 增加一件0.5磅重量的商品会产生什么影响？

• 需要更加细粒化容量的递增序列，间隔为0.5

Q6. 是否允许偷走物品一部分

• 动态规划只可计算物品整体的拿与不拿
• 但是，贪婪算法可以计算拿走物品一部分的结果，因为每次拿走容量范围内的最大价值物品。

Q7. 旅游行程最优化问题

在2天时间内旅游，给定多个景点需要花费的时间和想去参观的评分

• 利用动态规划算法计算出最优参观景点，即在规定时间内选择多个景点，使得意愿评分最高

Q8. 处理相互依赖情况

接着Q7问题，加入到巴黎铁塔和卢浮宫景点，各需要1.5天（其中都包含了从英国到巴黎花费的半天时间）

• 对于相互依赖问题，动态规划无法解决
• 动态规划要求每个子问题都是离散的

Q9. 计算最终的解时会涉及两个以上的子背包吗？

• 动态规划算法设计最多只需要合并两个子背包
• 不过子背包中可能包含另外两个子背包

Q10. 最优解可能导致背包没装满吗？

• 可能，价值很高的物品，空余的空间的填充价值不足以与此物品比价

9.3 最长公共字串

• 动态规划可以帮助你在给定约束条件下找到最优解。背包问题中：在给定背包容量情况下偷到价值最高的商品
• 当问题可分解为彼此独立且离散的子问题时就可使用动态规划来解决

设计动态规划解决方案Tips：

• 每种动态规划方案都涉及到网络
• 单元格中的值通常就是你要优化的值（商品价值）
• 每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网络的坐标轴

！【TODO】