不想写也要写!!!
概述
梯度下降法(Gradient Descent, GD)是一个最优化算法,常用于机器学习和人工智能当中用来迭代性地逼近最小偏差模型,其表达式为:
其中代表的是时刻
模型的参数,
表示学习因子,即下降的步长,
代表
处的梯度。
在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。
前置知识
梯度
梯度的本意是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向变化最快,变化率最大。以二元函数为例,设其在平面区域D上具有一阶连续偏导数,则其在点
处的梯度为:
泰勒展开式
函数在
处的泰勒展开式为:
其中,表示
的n阶导数,
是泰勒展开式的余项,是
的高阶无穷小。
数学推导
梯度下降法公式可由一阶泰勒展开式推导得到,取函数在
处的一阶泰勒展开式:
若很接近
,则
趋于0,可得到如下近似:
由上述公式可以得到与
之间的关系:
记,
为一常量,梯度下降法希望函数
的值不断减小,故有:
当取最小值时,
与
差最大,即下降速度最快,而:
当,即参数变化方向与梯度方向相反时上式取最小值,故可取
,得:
再令,可得到梯度下降法的递推公式:
通过控制参数可以控制
和
的差距,梯度下降法省略了
,实际上如果
和
的差距过大,
不可当作0省略,所以梯度下降法的步长不能太大,步长越大偏差也就越大。
算法流程
- 给定待优化连续可微函数
、学习率
以及一组初始值
;
- 计算梯度:
;
- 迭代更新:
;
- 计算梯度向量的模来判断算法是否收敛:
;
- 若收敛或超出最大迭代次数,则算法停止,否则重复234继续迭代更新;
实验示例
代码
import numpy as npimport matplotlib.pyplot as pltdef demo_2d():def f(x_):return x_ ** 2def grad(x_):return 2 * x_def delta_grad(x_, alpha=0.5):g = grad(x_)return alpha * galphas = [0.1, 0.3, 0.5, 0.8]threshold = 1e-10res = []for alpha in alphas:x = 5p_x = [x]for _ in range(100):delta = delta_grad(x, alpha)if abs(delta) < threshold:breakx = x - deltap_x.append(x)res.append(p_x)X = np.arange(-5, 5, 0.2)plt.figure()for i, _ in enumerate(res):plt.subplot(2, 2, i + 1)plt.plot(X, f(X))plt.plot(res[i], f(np.array(res[i])), 'r*-')plt.title(f'alpha={alphas[i]}')plt.tight_layout()plt.show()def demo_3d():def f(x_, y_):return 0.6 * (x_ + y_) ** 2 - x_ * y_def grad(x_, y_):return np.matrix([0.6 * 2 * (x_ + y_) - y_, 0.6 * 2 * (x_ + y_) - x_])def delta_grad(x_, y_, alpha=0.5):g = grad(x_, y_)return alpha * gx = np.matrix([[4], [4]])threshold = 1e-10p_x = [x[0, 0]]p_y = [x[1, 0]]for _ in range(100):delta = delta_grad(x[0, 0], x[1, 0])if abs(delta[0, 0]) < threshold and abs(delta[0, 1]) < threshold:breakx = x - deltap_x.append(x[0, 0])p_y.append(x[1, 0])x = np.linspace(-5, 5, 50)y = np.linspace(-5, 5, 50)X, Y = np.meshgrid(x, y)fig = plt.figure()ax = fig.add_subplot(111, projection='3d')ax.plot_surface(X, Y, f(X, Y), rstride=1, cstride=1, cmap=plt.cm.Greys)ax.plot(p_x, p_y, (f(np.array(p_x), np.array(p_y)) + 1), 'r*-')plt.show()
结果展示
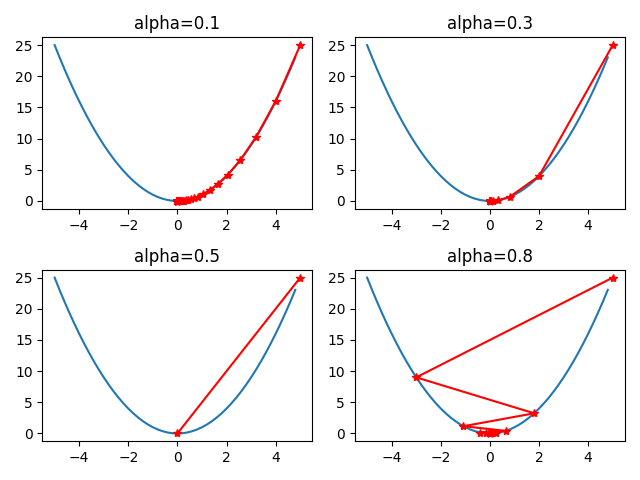
几种梯度下降算法
上面的两个例子用最简单的方式直观的展示了梯度下降算法的流程,需要注意的是,这两个例子中的和
是待更新的参数,而不是样本点,如第二个例子中:
,可以将其看成一个优化目标函数:
,其训练样本只有
这一个样本。
注:切勿将训练样本与训练参数混淆。迭代更新过程中是待更新的函数在不断变化去拟合样本,而不是样本在动,上面两个例子中标注的点的变化并不是样本点在变化。
下面以机器学习中一个常见的均方误差损失函数为例,介绍几种梯度下降算法,均方误差损失定义如下:
其中,为第
个样本的真实标注,
为第
个样本的预测结果,共
个训练样本,
是为了求导时与平方的
抵消系数,为方便起见,设预测函数为
,
代表
维样本集中第
个样本的第
个分量,
为参数集合,得到优化的目标函数为:
可以用梯度下降法优化这个函数,上面的例子展示了只有一个样本的梯度下降法流程,现在有个样本,根据不同的策略可以将梯度下降法大致分为下面三种:
- 批量梯度下降(Batch Gradient Descent, BGD)
- 随机梯度下降(Stochastic Gradient Descent, SGB)
- 小批量梯度(Mini Batch Gradient Descent, MBGD)
批量梯度下降
批量梯度下降法的思想最为直接,对所有样本计算梯度后求平均,来迭代更新参数。梯度计算公式为:
随机梯度下降
随机梯度下降在每次参数更新是从样本中只选取一个计算梯度,来迭代更新参数。梯度计算公式为:
从个样本中随机选取1个计算梯度,仅计算一个样本的梯度,且省略了求和及求平均的过程,降低了计算开销,因此提升了计算速度。
小批量梯度下降
小批量梯度下降则是上面两种方法的折中,从所有样本中选取一小部分计算梯度后求平均,来迭代更新参数。梯度计算公式为:
从个样本中随机选取个计算梯度。
优缺点对比
| 方法 | 优点 | 缺点 |
|---|---|---|
| 批量梯度下降 | 非凸函数可保证收敛至全局最优解 | 计算速度缓慢,不允许新样本中途进入 |
| 随机梯度下降 | 计算速度快 | 计算结果不易收敛,可能会陷入局部最优解中 |
| 小批量梯度下降 | 计算速度相对快,收敛相对稳定 | 小批量的规模的选取需探究 |
其实,已经有研究发现,当逐渐减小SGD方法使用的学习率时,可以保证SGD解的收敛性,但不一定保证收敛至全局最优解。此外,许多深度学习方法所使用的求解算法都是基于MBGD的,该方法一个算不上缺点的“缺点”就是需要找到合适的参与梯度计算的样本规模,对于超过2000个样本的较大数据集而言,参与计算的样本规模建议值为至。