关于熵的一些概念

熵

随机变量，概率分布，(非真实)概率分布

定义：

交叉熵

定义：

性质：

• 非对称性：

为什么分类任务中不用MSE损失而用交叉熵损失？

• 交叉熵使用softmax函数在梯度下降时能避免MSE学习速率降低的问题，因为MSE偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失，而使用交叉熵作为损失函数则不会导致这样的情况发生
• 损失函数目标角度讲，MSE认为平均总比有倾向性要好，但实际类别应具备不同倾向

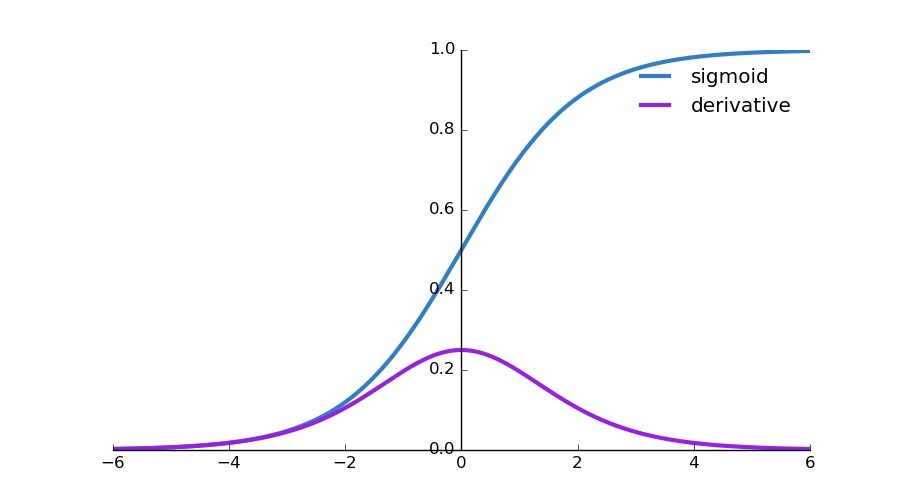
（图片来源：https://zhuanlan.zhihu.com/p/35707643）

KL散度（相对熵）

定义：

性质：

• 非负性：
• 非对称性：

注：当为常量时，KL散度和交叉熵基本等价，由于有监督训练中标签信息不会发生变化故其熵不会发生变化，此时KL散度和交叉熵作为损失函数理论上等价。而对于一些无监督训练如不确定性估计，预测的结果会发生变化熵也会变化，此时KL散度和交叉熵是有区别的（常用KL散度）。

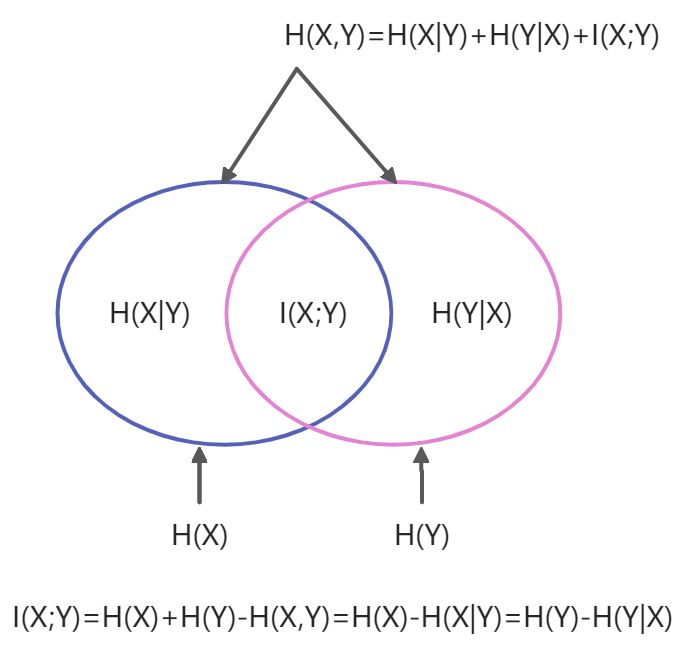
条件熵

随机变量、，边缘概率分布，，联合概率分布

定义：

性质：

互信息

定义：

性质：

• 对称性：
• 半正定：

参考

• 如何通俗的解释交叉熵与相对熵？
• 为什么交叉熵（cross-entropy）可以用于计算代价？
• 一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉
• 直观理解为什么分类问题用交叉熵损失而不用均方误差损失?
• 通俗理解条件熵
• 什么是「互信息」？