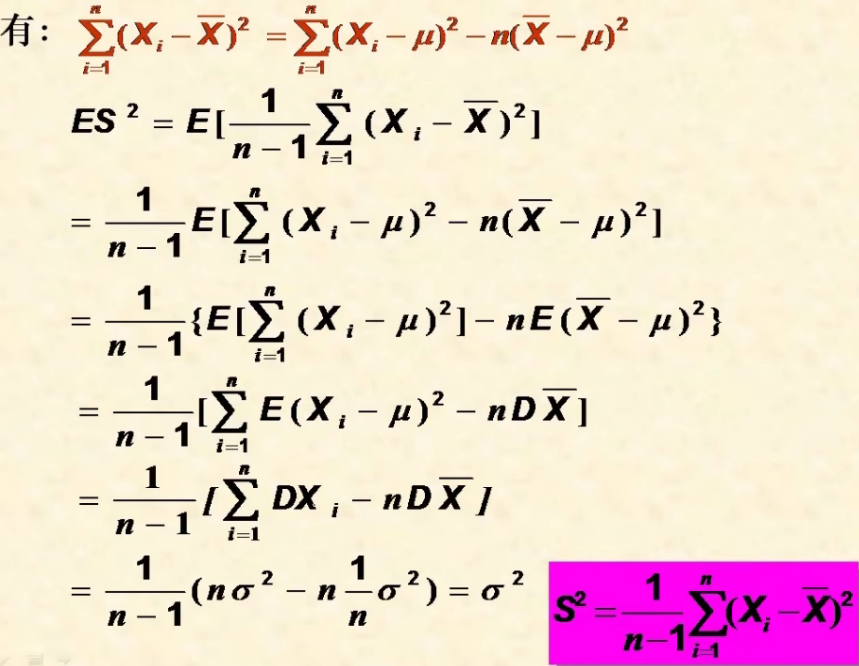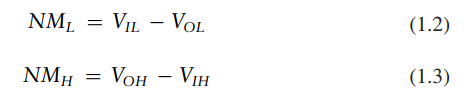1.4 NUMBER SYSTEMS

1 . 4 . 2 Binary Numbers

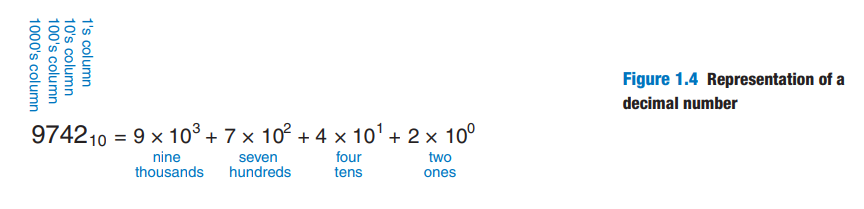
Example 1.2 DECIMAL TO BINARY CONVERSION

1. Convert the decimal number 8410 to binary

%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20transform%3D%22translate(19776%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-38%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-34%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%222223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%223002%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(19776%2C-1200)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-34%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%222223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%223002%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(19776%2C-2400)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%222223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%223002%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(19776%2C-3600)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%222223%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%223002%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(20026%2C-4800)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-35%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%22722%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221723%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%222501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(20026%2C-6000)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%22722%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221723%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%222501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(20026%2C-7200)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%22722%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%221723%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%222501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(14266%2C-8420)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-45%22%20x%3D%22759%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%221524%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-45%22%20x%3D%222293%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%223058%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-53%22%20x%3D%223817%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-45%22%20x%3D%224463%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-27F9%22%20x%3D%225505%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(7421%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%221501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%222002%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%222502%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%223003%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%224954%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%2211656%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(12713%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-38%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-34%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1001%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=84—0%5C%5C%0A42—0%5C%5C%0A21—1%5C%5C%0A10—0%5C%5C%20%20%20%20%20%20%0A5—1%5C%5C%0A2—0%5C%5C%0A1—1%5C%5C%0AREVERSE%5CLongrightarrow1010100%7B2%7D%3D84%7B10%7D&id=m8De7)

1. Convert 0.5310 to binary

1 . 4 . 3 Hexadecimal Numbers

Example 1.3 HEXADECIMAL TO BINARY AND DECIMAL CONVERSION

1. Convert the hexadecimal number to binary and to decimal.

   Each hexadecimal digit directly corresponds to 4 binary digits. So

Hexadecimal => Decimal

Example 1.4 BINARY TO HEXADECIMAL CONVERSION

1. Convert the binary number 1111010 to hexadecimal.

   Start from the right. 4 least significant btis 1010=A, 111=7.Hence, 1111010=7A

Example 1.5 DECIMAL TO HEXADECIMAL CONVERSION

1. Convert the decimal number 333 to hexadecimal and binary.

1 . 4 . 4 Bytes, Nibbles, and All That Jazz

8 bits => 1 byte
4 bits => 1 _nibblethe term is cute _1 hexadecimal stores 1 nibble

Microprocessors handle data in chunks called words

1 . 4 . 5 Binary Addition

3/15/2022:

• Positive
  • binary = magnitude = complement
• Negative
  • magnitude = inverting the bits in the number(positive binary
  • complement = magnitude + 1 _reversing the sign _method

    Example 1.8 ADDITION WITH OVERFLOW

1. Compute 1101 + 0101. Does overflow occur?

   The msb is discarded

1 . 4 . 6 Signed Binary Numbers

Sign/Magnitude Numbers

Match our custom, unfortunately, ordinary binary addition does not work for sign/magnitude numbers. For example, using ordinary addition on -5 + 5 gives 1101 + 0101 = 10010, which is nonsense.
An N-bit sign/magnitude number spans the range
11…111-(10..000-1) ~ 01…11110..000-1
Sign/magnitude numbers are slightly odd in that both +0 and -0 exist.Both indicate zero.

Two’s Complement Numbers

zero is written as all zeros:
00…000
The most positive number has a 0 in the msb and 1’s elsewhere:
01…111 = 2N-1 - 1
The most negative number has a 1 in the msb and 0’s elsewhere:
10…000 = -2N-1
And -1 is written as all ones: 11…111.
msb can be viewed as the sign bit.(1:negative;0:positive
P.S. msb is discarded because the result is stored in 4 bits, having 10000=(weird number
the range of an N-bit two’s complement number spans

overflow occurs if the two numbers being added have the same sign bit and the result has the opposite sign bit.

Example 1.14 ADDING TWO’S COMPLEMENT NUMBERS WITH OVERFLOW

Compute 4 + 5 using 4-bit two’s complement numbers. Does the result overflow?

01002+01012=10012=-710 If the computation had been done using five or more bits, the result 01001 = 9 would have been correct.

When a two’s complement number is extended to more bits, the sign bit must be copied into the msb positions. This process is called sign extension.

Comparison of Number Systems

Unsigned numbers span the range [0, 15]
Two’s complement numbers span the range [-8, 7]
Sign/magnitude numbers span the range [-7, 7] 0 is represented by both 0000 and 1000.
N-bit sign/magnitude numbers represent only 2N - 1 integers
N-bit unsigned binary or two’s complement numbers represent 2N integers.

1.5 LOGIC GATES

1 . 5 . 1 NOT Gate

“Y equals NOT a”
※Also called an inverter

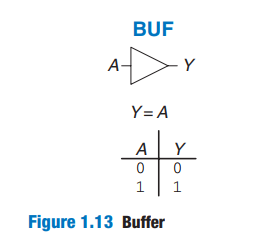
1 . 5 . 2 Buffer

simply copies the input to the output. Ability to deliver large amounts of current to a motor or the ability to quickly send its output to many gates.

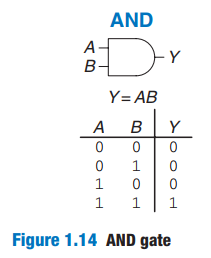
1 . 5 . 3 AND Gate

Y = A ∩ B. The ∩ symbol is pronounced “intersection” and is preferred by logicians. We prefer Y = AB,read “Y equals A and B,” because we are lazy.

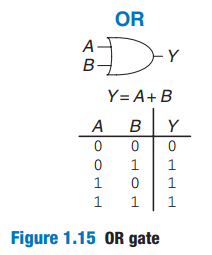
1 . 5 . 4 OR Gate

Y = A + B or Y = A ∪ B. The ∪ symbol is pronounced union
Y = A + B is pronounced “Y equals A or B. “

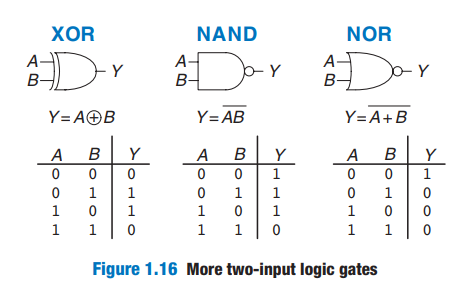
1 . 5 . 5 Other Two-Input Gates

Any gate can be followed by a bubble to invert its operation.

• XOR (exclusive OR, pronounced “ex-OR”)
  • 
  • N-input XOR gate is sometimes called parity gate, output is true when odd number of true inputs
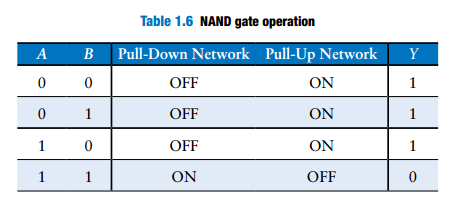
• NAND(NOT AND)
  • 
• NOR(NOT OR)
  • 

Using two _inverters _and a two-input AND gate, shown in Figure 2.11(a) as the NOR function from Section 1.5.5:

Example 1.15 XNOR GATE

• Figure 1.17 shows the symbol and Boolean equation for a two-input XNOR (pronounced ex-NOR) gate that performs the inverse of an XOR. Complete the truth table.
• 

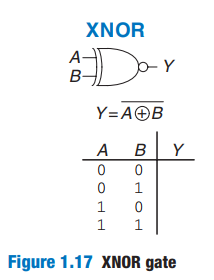
• Solution:
  • combining the Exclusive-OR gate (XOR gate) and the NOT gate | A | B | Y | | —- | —- | —- | | 0 | 0 | 1 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 1 |

1 . 5 . 6 Multiple-Input Gates

AND, OR, XOR, NAND, NOR, and XNOR

1.6 BENEATH THE DIGITAL ABSTRACTION

From continuous to discrete.

1 . 6 . 1 Supply Voltage

Lowest voltage is 0 V, AKA groud _or GND_
Highest VDD (decreasing, avoid overloading the transistors

1 . 6 . 2 Logic Levels

mapping of a continuous variable onto a discrete binary variable is done by defining logic levels VOH, VOL, VIH, and VIL are called the output and input high and low logic levels

NM & Forbidden Zone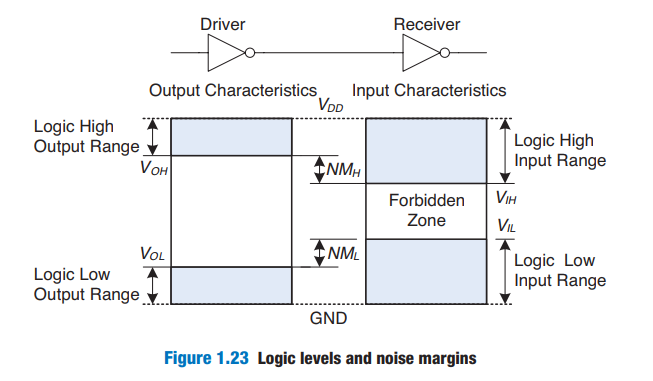

※VDD stands for the voltage on the drain of a semiconductor
VCC : power supply; voltage on the collector of a transistor
VSS : ground; because it is the voltage on the source of a transistor

1 . 6 . 3 Noise Margins

_noise margin (NM) _is the amount of noise that could be added to a worst-case output such that the signal can still be interpreted as a valid input.

respectively:

1 . 6 . 4 DC Transfer Characteristics so dumb

Term’s historical root comes from direct current

The DC transfer characteristics of a gate describe the output voltage as a function of the input voltage when the input is changed slowly enough that the output can keep up.
It’s not the same to the example above!!!

Ideal : abrupt switching threshold at VDD/2 Real inverter: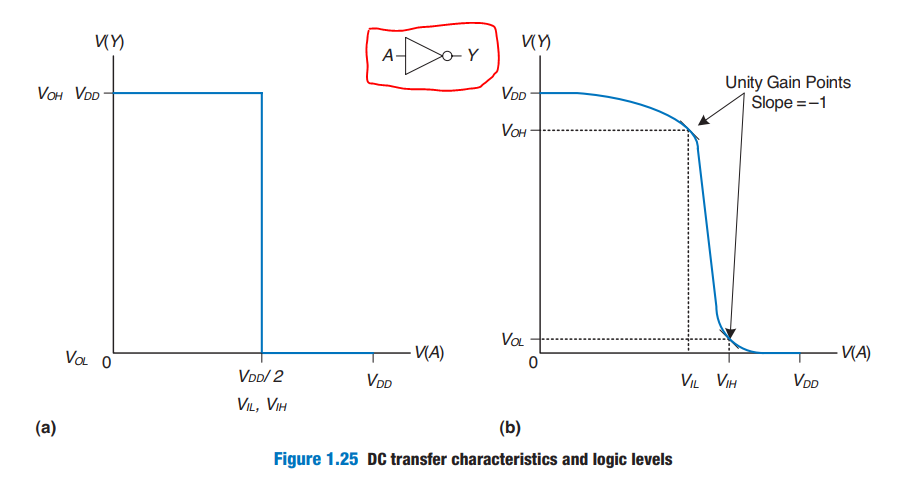

Choosing logic level_s at the **_unity gain points** usually maximizes the noise margins. If VIL were reduced, VOH would only increase by a small amount. But if VIL were increased, VOH would drop precipitously.
dV(Y)/dV(A)=-1

1 . 6 . 5 The Static Discipline

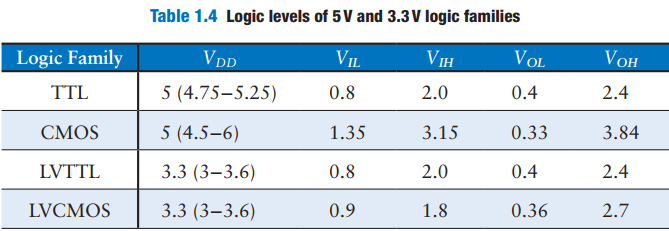
Logical gates are designed to conform to the static discipline . Digital designers sacrifice the freedom of using arbitrary analog circuit elements Transistor-Transistor Logic (TTL), Complementary MetalOxide-Semiconductor Logic (CMOS, pronounced sea-moss), Low Voltage TTL Logic (LVTTL), Low Voltage CMOS Logic (LVCMOS). Their logic levels are compared in Table 1.4.

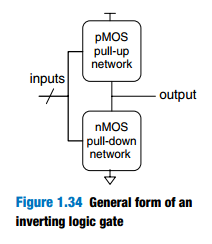
1.7 CMOS TRANSISTORS*

Transistors are electrically controlled switches that turn ON or OFF when a voltage or
current is applied to a control terminal.

The two main types of transistors are bipolar junction transistors and metal-oxide-semiconductor field
__effect transistors (MOSFETs or MOS transistors, pronounced “mossfets” or “M-O-S”,respectively).

1 . 7 . 1 Semiconductors

1 . 7 . 2 Diodes

forward bised

1 . 7 . 3 Capacitors

A capacitor consists of two conductors separated by an insulator.

1 . 7 . 4 nMOS and pMOS Transistors

MOSFETs are built on thin, flat _wafers _of silicon.
A MOSFET behaves as a voltage-controlled switch in which the gate voltage creates an electric field that turns ON or OFF a connection between the source and drain.
The substrate of an nMOS transistor is normally tied to GND, the lowest voltage in the system. First, consider the situation when the gate is also at 0V, as shown in Figure 1.30(a). The diodes between the source or drain and the substrate are reverse biased because the source or drain voltage is nonnegative. Hence, there is no path for current to flow between the source and drain, so the transistor is OFF. Now, consider when the gate is raised to VDD, as shown in Figure 1.30(b).

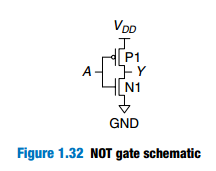
1 . 7 . 5 CMOS NOT Gate

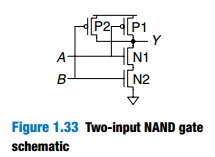
1 . 7 . 6 Other CMOS Logic Gates

1 . 7 . 7 Transmission Gates

1 . 7 . 8 Pseudo-nMOS Logic

1.8 POWER CONSUMPTION*

1.9 SUMMARY AND A LOOK AHEAD

nMOS transistors turn ON when the gate is 1. pMOS transistors turn ON when the gate is 0