解题过程

:::info 题目链接
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。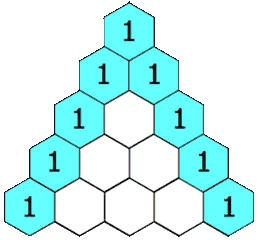
image.png :::

  1. /**
  2.  * @link https://leetcode.cn/problems/pascals-triangle/
  3.  * @title 118. 杨辉三角
  4.  * @description 给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。
  5.  * 在「杨辉三角」中，每个数是它左上方和右上方的数的和。
  6.  * @param {number} numRows
  7.  * @return {number[][]}
  8.  */
  9. // 解法一：找规律法
  10. // 思路：第一行和第二行是没有规律的，第三行开始才有，且二维数组元素数组首尾都是1，所以第三行开始，除首尾外，当前行元素(i)值为上一行元素左上角(i-1)+右上角(i)的值，即元素索引是存在对应关系的（题目核心重点关键）
  11. var generate = function (numRows) {
  12.   const resultNums = []
  14.   for(let i = 0; i < numRows; i++) {
  15.     if (i === 0) {
  16.       // 第一行是固定的
  17.       resultNums.push([1])
  18.     } else if (i === 1) {
  19.       // 第二行也是固定
  20.       resultNums.push([1, 1])
  21.     } else {
  22.       // 第三行开始有规律
  23.       const nums = []
  24.       for (let j = 0; j <= i; j++) {
  25.         if (j === 0 || j === i) {
  26.           // 首尾为1
  27.           nums.push(1)
  28.         } else {
  29.           // 获取上一行的值
  30.           const preNums = resultNums[i - 1]
  31.           // 当前元素索引值与上一行数组元素索引值关系相加得出
  32.           const currNum = preNums[j - 1] + preNums[j]
  33.           nums.push(currNum)
  34.         }
  35.       }
  37.       resultNums.push(nums)
  38.     }
  39.   }
  41.   return resultNums
  42. }
  44. // 第二版优化
  45. // var generate = function (numRows) {
  46. //   const resultNums = []
  48. //   for (let i = 0; i < numRows; i++) {
  49. //     const nums = []
  50. //     for (let j = 0; j <= i; j++) {
  51. //       if (j === 0 || j === i) {
  52. //         // 首尾为1
  53. //         nums.push(1)
  54. //       } else {
  55. //         // 获取上一行的值
  56. //         const preNums = resultNums[i - 1]
  57. //         // 当前元素索引值与上一行数组元素索引值关系相加得出
  58. //         const currNum = preNums[j - 1] + preNums[j]
  59. //         nums.push(currNum)
  60. //       }
  61. //     }
  63. //     resultNums.push(nums)
  64. //   }
  66. //   return resultNums
  67. // }
  70. // 第三版优化后的代码
  71. var generate = function (numRows) {
  72.   const resultNums = []
  74.   for (let i = 0; i < numRows; i++) {
  75.     const nums = []
  76.     for (let j = 0; j <= i; j++) {
  77.       // 获取上一行的值
  78.       const preNums = i === 0 ? [] : resultNums[i - 1]
  79.       // 当前元素索引值与上一行数组元素索引值关系相加得出
  80.       const pre = j - 1 >= 0 ? preNums[j - 1] : 0
  81.       const cur = j < preNums.length ? preNums[j] : 0
  82.       const currNum = pre === 0 && cur === 0 ? 1 : pre + cur
  83.       nums.push(currNum)
  84.     }
  86.     resultNums.push(nums)
  87.   }
  89.   return resultNums
  90. }
  92. // const result = generate(5)
  93. const result = generate(1)
  94. console.log(result)

解题感受

这一题偏向数学方面计算的逻辑关系，题目看了很多遍才找到的规律，重点理解当前行元素i的值等于上一行第i位置元素值加上第i-1位置的和，代码没有去除首尾判断的简写了，没有优化到计算里面去，后续可以优化一下，找到规律就很容易，看了官方也有其他一些方法可以解答

参考答案

错一位再逐个相加