1.获取数据，定义问题

数据介绍：http://archive.ics.uci.edu/ml/datasets/Combined+Cycle+Power+Plant
数据下载地址：http://archive.ics.uci.edu/ml/machine-learning-databases/00294/
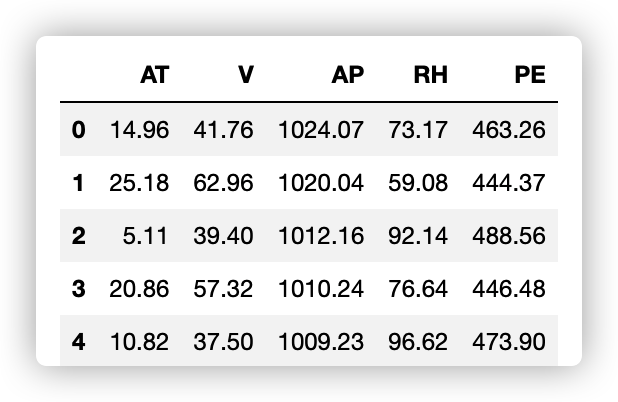
里面是一个循环发电场的数据，共有9568个样本数据，每个数据有5列，分别是:AT（温度）, V（压力）, AP（湿度）, RH（压强）, PE（输出电力)。我们不用纠结于每项具体的意思。
我们的问题是得到一个线性的关系，对应PE是样本输出，而AT/V/AP/RH这4个是样本特征， 机器学习的目的就是得到一个线性回归模型，即:

而需要学习的，就是这5个参数。

2.整理数据

3.Pandas读取数据

倒入依赖库

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets, linear_model

读取数据

data = pd.read_csv("./data/CCPP/CCPP.csv")
data.head()

4. 准备运行算法的数据

X = data[["AT", "V", "AP", "RH"]]
X

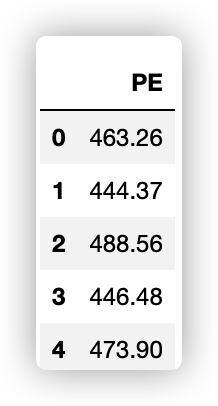
Y = data[["PE"]]
Y.head()

5. 划分训练集和测试集

from sklearn.cross_validation import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state = 1)
print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
print(Y_test.shape)

6. 运行scikit-learn的线性模型

from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(X_train, Y_train)
print(linreg.intercept_)
print(linreg.coef_)
# Output:
[460.05727267]
[[-1.96865472 -0.2392946   0.0568509  -0.15861467]]

7. 模型评价

我们需要评估我们的模型的好坏程度，对于线性回归来说，我们一般用均方差（Mean Squared Error, MSE）或者均方根差(Root Mean Squared Error, RMSE)在测试集上的表现来评价模型的好坏。

#模型拟合测试集
Y_pred = linreg.predict(X_test)
from sklearn import metrics
# 用scikit-learn计算MSE
print("MSE:%d",metrics.mean_squared_error(Y_test, Y_pred))
# 用scikit-learn计算RMSE
print("RMSE:%data",np.sqrt(metrics.mean_squared_error(Y_test, Y_pred)))
# Output:
MSE:%d 20.83719154722035
RMSE:%data 4.564777272465805

8. 交叉验证

from sklearn.model_selection import cross_val_predict
predicted = cross_val_predict(linreg, X, Y, cv= 10)
# 用scikit-learn计算MSE
print("MSE:%d",metrics.mean_squared_error(Y, predicted))
# 用scikit-learn计算RMSE
print("RMSE:%data",np.sqrt(metrics.mean_squared_error(Y, predicted)))
# Output:
MSE:%d 20.793672509857537
RMSE:%data 4.560007950635343

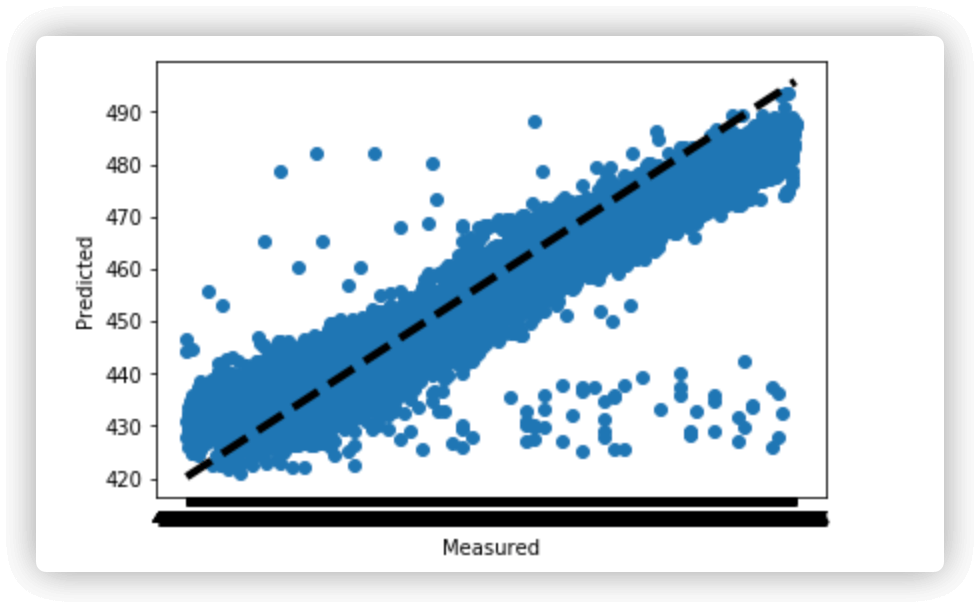
9. 画图观察结果

fig, ax = plt.subplots()
ax.scatter(y, predicted)
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measured')
ax.set_ylabel('Predicted')
plt.show()