目录
1 数组
2 链表
3 栈和队列
4 二叉树
5 堆和堆栈
6 散列表
7 红黑树
数组是一种连续存储线性结构,元素类型相同,大小相等,数组是多维的,通过使用整型索引值来访问他们的元素,数组尺寸不能改变。
- 数组的优点:
存取速度快 - 数组的缺点:
事先必须知道数组的长度
插入删除元素很慢
空间通常是有限制的
需要大块连续的内存块
插入删除元素的效率很低
n 个节点离散分配,彼此通过指针相连,每个节点只有一个前驱节点,每个节点只有一个后续节点,首节点没有前驱节点,尾节点没有后续节点。
确定一个链表我们只需要头指针,通过头指针就可以把整个链表都能推出来。
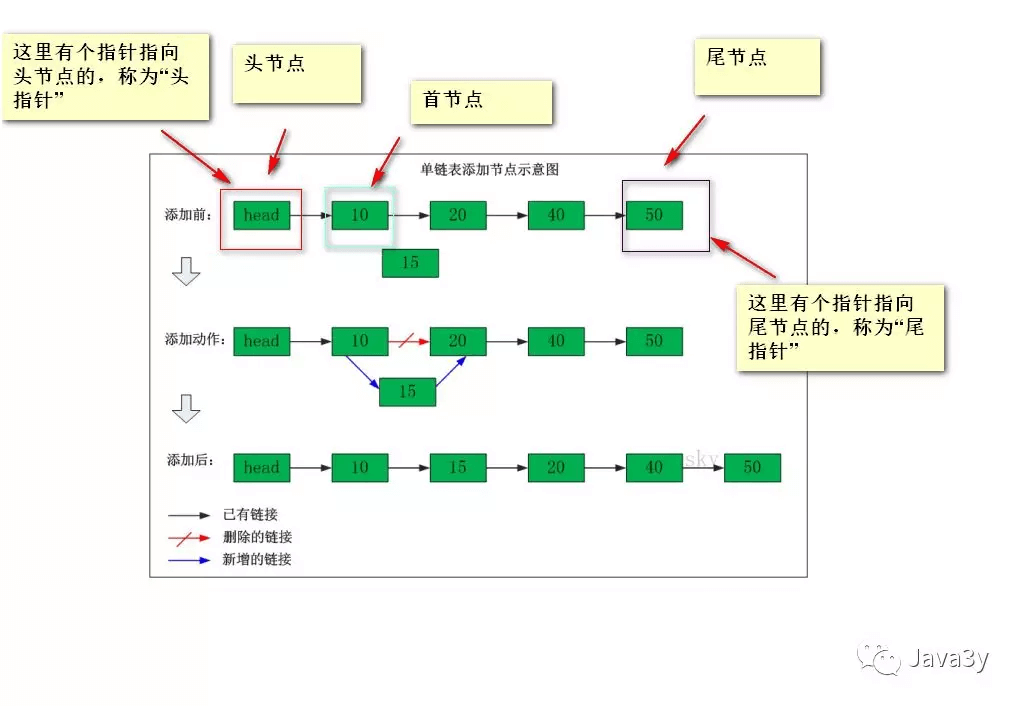
链表
- 链表优点
空间没有限制
插入删除元素很快 - 链表缺点
存取速度很慢
链表又细分了 3 类:
- 单向链表
一个节点指向下一个节点。 - 双向链表
一个节点有两个指针域。 - 循环链表
能通过任何一个节点找到其他所有的节点,将两种 (双向 / 单向) 链表的最后一个结点指向第一个结点从而实现循环。
操作链表要时刻记住的是:节点中指针域指向的就是另一个节点!
Java 实现链表
首先,我们定义一个类作为节点,节点需要有两个属性:
数据域
指针域
public class Node {public int data;public Node next;public Node() {}public Node(int data) {this.data = data;}public Node(int data, Node next) {this.data = data;this.next = next;}}
如上,一个链表节点对象就创建完成了,但理解链表本身并不难,但做相关的操作却并非易事,其算法包括且不限于:
- 插入节点
- 遍历
- 查找
- 清空
- 销毁
- 求长度
- 排序
- 删除节点
- 去重
创建链表 & 增加节点
创建头节点Node head = new Node(value);
然后找到尾节点进行插入
public static void addData(int value, Node head) {Node newNode = new Node(value);Node temp = head;while (temp.next != null) {temp = temp.next;}temp.next = newNode;}
遍历链表
上面我们已经编写了增加方法,现在遍历一下,从首节点开始,不断往后面找,直到后面的节点没有数据
public static void traverse(Node head) {Node temp = head.next;while (temp != null) {System.out.println("链表数据:" + temp.data);temp = temp.next;}}
其他算法略,读者朋友们可自行练习。
数组和链表都是线性存储结构的基础,栈和队列都是线性存储结构的应用。
栈
我们将栈可以看成一个放光盘的箱子,箱口与略大与光盘。然后
- 往箱子里面放东西叫做入栈
- 往箱子里面取东西叫做出栈
- 箱子的底部叫做栈底
- 箱子的顶部叫做栈顶
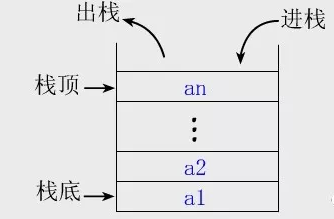
栈
说到栈的特性,有一句经典的言语来概括:先进后出,后进先出。
Java 实现栈
- 使用数组实现的叫
静态栈 - 使用链表实现的叫
动态栈
沿用上一章节的链表对象 Node,创建一个栈对象 (栈顶,栈底):
public class Stack {``` public Node stackTop;
public Node stackBottom;
public Stack(Node stackTop, Node stackBottom) { this.stackTop = stackTop; this.stackBottom = stackBottom; }
public Stack() { }
<br />}<a name="db17cd65"></a>##### 进栈操作将原本栈顶指向的节点交由新节点来指向,栈顶指向新加入的节点
public static void pushStack(Stack stack, int value) {
Node newNode = new Node(value);newNode.next = stack.stackTop;stack.stackTop = newNode;
}
<a name="3cda4915"></a>##### 遍历栈只要栈顶元素的指针不指向栈底,那么就一直输出遍历结果
public static void traverse(Stack stack) { Node stackTop = stack.stackTop;
while (stackTop != stack.stackBottom) {System.out.println("栈数据:" + stackTop.data);stackTop = stackTop.next;}
}
<a name="eed40543"></a>##### 出栈操作在出栈之前看看该栈是否为空,不为空才出栈<br />将栈顶的元素的指针 (指向下一个节点) 赋值给栈顶指针(完成出栈)
public static void popStack(Stack stack) {
if (stack.stackTop != stack.stackBottom) {Node top = stack.stackTop;stack.stackTop = top.next;System.out.println("栈数据:" + top.data);}
}
---<a name="0796f7f8"></a>### 队列队列非常好理解,我们将队列可以看成我们平时排队打饭。- 有新的人加入了 -> 入队- 队头的人打饭了 -> 出队相对于栈而言,队列的特性是:先进先出,后进后出队列- 使用数组实现的叫`静态队列`- 使用链表实现的叫`动态队列`<br />这次我就使用数组来实现静态队列。<br />[图片上传失败...(image-cefdbb-1540348423645)]<a name="79d0edb7"></a>##### Java 实现队列
public class Queue
private int rear;
public Queue(){this(5);}public Queue(int initialSize){if(initialSize >=0){this.maxSize = initialSize;data = new Object[initialSize];front = rear =0;}else{throw new RuntimeException("初始化大小不能小于0:" + initialSize);}}public boolean empty(){return rear==front?true:false;}public boolean add(E e){if(rear== maxSize){throw new RuntimeException("队列已满,无法插入新的元素!");}else{data[rear++]=e;return true;}}public E poll(){if(empty()){throw new RuntimeException("空队列异常!");}else{E value = (E) data[front];data[front++] = null;return value;}}public int length(){return rear-front;}public static void traverseQueue(Queue queue) {int i = queue.front;while (i != queue.rear) {System.out.println("队列值:" + queue.data[i]);i = (i + 1) % queue.data.length;}}
}
其他队列算法、循环队列、链表结构的队列实现略,读者朋友可自行练习。树是一种非线性的数据结构,相对于线性的数据结构 (链表、数组) 而言,树的平均运行时间更短(往往与树相关的排序时间复杂度都不会高),<br />和现实中的树相比,编程的世界中的树一般是 “倒” 过来看,这样容易我们分析。树现实中的树是有很多很多个分支的,分支下又有很多很多个分支,如果在程序中实现这个会非常麻烦。因为本来树就是非线性的,而我们计算机的内存是线性存储的,太过复杂的话无法设计出来。<br />因此,就有了简单又经常用的 -> 二叉树,顾名思义,就是每个分支最多只有两个的树,上图就是二叉树。- 一棵树至少会有一个节点 (根节点)- 树由节点组成,每个节点的数据结构包括一个数据和两个分叉<br /><br />a 空二叉树, b 只有一个根结点, c 只有左子树, d 只有右子树, e 完全二叉树<a name="0b411a6b"></a>##### Java 实现二叉树首先,使用 Java 类定义节点
public class TreeNode {
private int value;private TreeNode leftNode;private TreeNode rightNode;public TreeNode(int value) {this.value = value;}
}
我们目标是实现如下图的树目标树第一步:创建 5 个节点
TreeNode treeNode1 = new TreeNode(10);
TreeNode treeNode2 = new TreeNode(9);
TreeNode treeNode3 = new TreeNode(20);
TreeNode treeNode4 = new TreeNode(15);
TreeNode treeNode5 = new TreeNode(35);
它们目前的状态分散的,需要把这 5 个节点连接起来
treeNode1.setLefNode(treeNode2); treeNode1.setRightNode(treeNode3);
treeNode3.setLeftNode(treeNode4); treeNode3.setRightNode(treeNode5);
<a name="060ba7aa"></a>##### 遍历二叉树二叉树遍历有三种方式:- 中序遍历<br />先访问根节点,然后访问左节点,最后访问右节点 (根 -> 左 ->右)- 先序遍历<br />先访问左节点,然后访问根节点,最后访问右节点 (左 -> 根 ->右)- 后序遍历<br />先访问左节点,然后访问右节点,最后访问根节点 (左 -> 右 ->根)以上面的二叉树为例:- 如果是中序遍历:10->9->20->15->35- 如果是先序遍历:9->10->15->20->35<br />解释:访问完 10 节点过后,去找的是 20 节点,但 20 下还有子节点,因此先访问的是 20 的左节点 15 节点。由于 15 节点没有子节点了。所以就返回 20 节点,访问 20 节点。最后访问 35 节点- 如果是后序遍历:9->15->35->20->10<br />解释:先访问 9 节点,随后应该访问的是 20 节点,但 20 下还有子节点,因此先访问的是 20 的左节点 15 节点。由于 15 节点没有子节点了。所以就去访问 35 节点,由于 35 节点也没有子节点了,所以返回 20 节点,最终返回 10 节点一句话总结:中序 (根 -> 左 ->右),先序 (左 -> 根 ->右),后序 (左 -> 右 ->根)。如果访问有孩子的节点,先处理孩子的,随后返回- 每个节点的遍历如果访问有子节点的节点,先处理子节点的 (逻辑是一样的)- 因此遍历的方法是递归- 递归的出口就是:当没有子节点了,结束遍历因此,我们可以写出这样的中序遍历代码:
public static void inTraverseBTree(TreeNode rootTreeNode) {
if (rootTreeNode != null) {System.out.println(rootTreeNode.getValue());inTraverseBTree(rootTreeNode.getLeftNode());inTraverseBTree(rootTreeNode.getRightNode());}
} ```
先序遍历和后序遍历略…
练习:查找树深度、查找最大值、查找树节点数量。
这些算法都会用到了递归,读者朋友练习这些算法的时候需要熟练掌握递归,递归在非线性的数据结构中是用得非常多。
树的应用也非常广泛,此篇也只是非常简单地说明了树的数据结构。
堆内存用来存放由 new 创建的对象和数组。
在堆中分配的内存,由 Java 虚拟机的自动垃圾回收器来管理。
‘堆栈’ 就是 ‘栈’,称呼不同而已。
栈的优势是,存取速度比堆要快,仅次于直接位于 CPU 中的寄存器。但缺点是,存在栈中的数据大小与生存期必须是确定的,缺乏灵活性。另外,栈数据可以共享。
堆的优势是可以动态地分配内存大小,生存期也不必事先告诉编译器,Java 的垃圾收集器会自动收走这些不再使用的数据。但缺点是,由于要在运行时动态分配内存,存取速度较慢。
无论是 Set 还是 Map,我们会发现都会有对应的 —>HashSet,HashMap
首先我们也先得回顾一下数据和链表:
- 链表和数组都可以按照人们的意愿来排列元素的次序,他们可以说是有序的 (存储的顺序和取出的顺序是一致的)
- 这会带来缺点:想要获取某个元素,就要访问所有的元素,直到找到为止,会消耗很多时间。
所以我们需要另外的存储结构:不在意元素顺序,能快速查找元素。其中就有一种常见方式:散列表。
散列表工作原理
散列表为每个对象计算出一个整数,称为散列码。根据这些计算出来的整数 (散列码) 保存在对应的位置上!即,散列码就是索引。
在 Java 中,散列表用的是链表数组实现的,每个列表称之为桶。
是一种平衡二叉树,TreeSet、TreeMap 底层都是红黑树来实现的。
二叉查找树也有个例 (最坏) 的情况(线性):
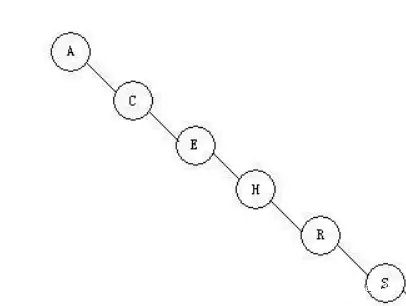
线性二叉查找树
上面符合二叉树的特性,但是它是线性的,完全没树的用处,树是要 “均衡” 才能将它的优点展示出来,比如下面这种:
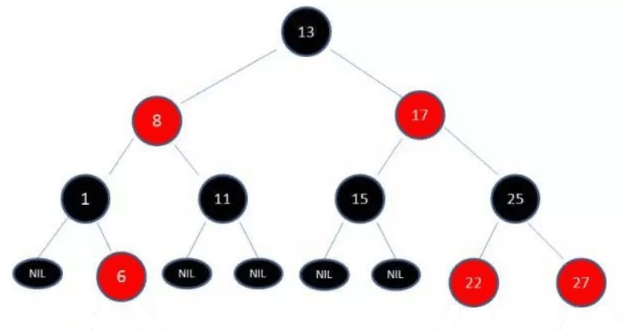
红黑树. png
因此,就有了平衡树这么一个概念~ 红黑树就是一种平衡树,它可以保证二叉树基本符合均衡的金字塔结构。
上图就是一个红黑树,红黑树就字面上的意思,有红色的节点,有黑色的节点。
- 性质 1. 节点是红色或黑色。
- 性质 2. 根节点是黑色。
- 性质 3. 每个叶节点(NIL 节点,空节点)是黑色的。
- 性质 4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 性质 5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
红黑树可以说是十分复杂,这里只介绍个概念,有兴趣的朋友可自行研究。
https://www.jianshu.com/p/8e54797ec3e0

