计算匹配双方相似的程度，另外再指定一个相似的限度不确定性性：
表示：

• 知识不确定性：专家系统中知识的不确定性一般是由领域专家给出的，通常用一个数值表示，它表示相应知识的不确定性程度，称为知识的静态强度。
• 证据不确定性：证据不确定性的表示方法与知识不确定性的表示方法一致，通常也用一个数值表示，代表相应的证据的不确定程度，称之为动态强度

不同的知识以及不同的证据，其确定性的程度一般是不相同的，需要用不同的数据表示其不确定性程度，同时还需事先规定它的取值范围

不确定性匹配算法及其阈值：
推理是一个不断运用知识的过程。为了找到所需的知识，需要运用知识的前提条件与数据库中已知的证据进行匹配，只有匹配成功的知识才有可能被应用。
计算匹配双方相似的程度，另外再指定一个相似的限度，相似度<指定限度（匹配成功）
组合证据：知识的前提条件既可以是简单条件，也可以是用 AND 或者 OR 将多个简单条件连接起来的复合条件。进行匹配时，一个简单条件对应于一个单一的证据，一个复合条件对应于一组证据，称这一组证据为组合证据
组合证据的不确定性计算方法：

• 最大最小方法
• hamacher方法
• 概率方法
• 有界方法

  可信度方法

  IF E THEN H (CF(H, E)) CF(H, E) 是该条件知识的可信度，称为可信度因子
  大于零：E对H为真的支持度
  小于零：E对H为真的不支持度

知识的不确定性表示：

不确定性因子的可信度度量 CF 满足： -1 ≤ CF(H, E) ≤ 1 H结论，E前提

• CF(H, E) = 1，前提为真，结论必为真
• CF(H, E) = -1，前提为真，结论必为假

• CF(H, E) = 0，前提的真假与结论无关

  证据的不确定性表示：

  证据 E 的可信度表示为 CF(E)，则同样有：-1 ≤ CF(E) ≤ 1

• CF(E) = 1，前提肯定为真

• CF(E) = -1，前提肯定为假
• CF(E) = 0，前提的真假一无所知
• CF(E) > 0，表示 E 以 CF(E) 程度为真
• CF(E) < 0，表示 E 以 CF(E) 程度为假

不确定性传递：

• E1 ∧ E2 → H， CF(E1 ∧ E2) = min{CF(E1), CF(E2)} 证据合取的可信度求各个证据最小
• E1 ∨ E2 → H， CF(E1 ∨ E2) = max{CF(E1), CF(E2)}
• CF(~E) = -CF(E)
• 结论H的可信度计算：E->H求得CF(H) = max(0, CF(E)) × CF(H, E)

结论不确定性合成算法：
由多条不同知识推出相同结论，但是可信度不同，可以求综合可信度

例题

模糊推理方法

隶属度：描述介于“真”和“假”中间的过程。隶属度是一个命题中所描述事物的属性、状态和关系等强度
论域：所讨论的全体对象称为论域，用大写字母表示；
元素：论域中的每个对象，通常用小写字母表示；
集合：论域中具有某种相同属性的确定的、可以彼此区别的元素的全体。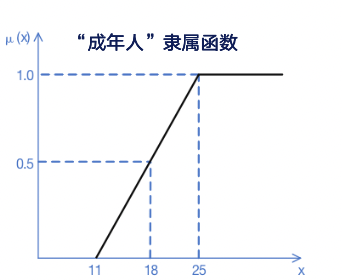

模糊集合

模糊集合关系运算

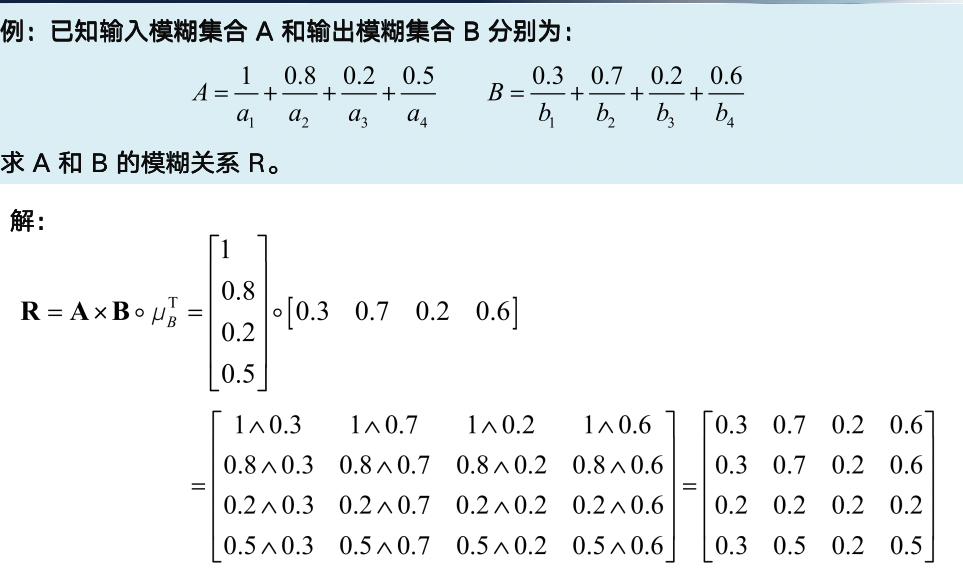
模糊关系

转置后，对应位置取最小就行

模糊关系合成

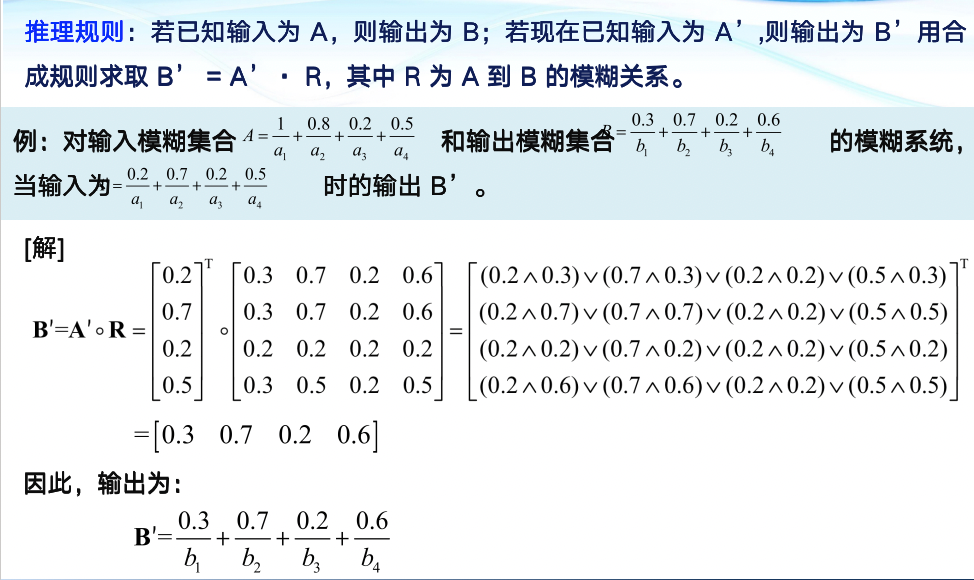
模糊推理

模糊决策

将模糊推理得到的模糊向量，转化为确定值的过程称为“模糊决策”，或者“模糊判决”

• 最大隶属度法

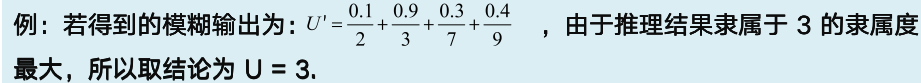
• 加权平均判别法
• 中位数法