搜索过程中需要解决的基本问题为:
- 完备性
- 最优性
- 复杂性
- 可行性
主要搜索过程分类
- 按照搜索方向
- 正向搜索——数据驱动
- 逆向搜索——目的驱动
- 双向搜索
- 按照是否使用启发式信息
- 盲目搜索
- 启发式搜索
状态空间知识表示
状态空间构成
- 状态 表示问题解法中每一步问题状况的数据结构。通常状态是一组变量或数组
- 算符 把问题从一个状态变换为另一个状态的手段。通常算符用来表示引起状态变化的过程型知识的一组关系或函数。
- 状态空间 (S, O, S0, G)
- 其中,S 表示状态集合;O 表示状态转换规则集合;S0 表示包含问题的初始状态;G 是包含问题的目标状态。
- 问题的解 有限的操作算子序列,它使初始状态转换为目标状态。
问题表示和求解
盲目的图搜索策略
搜索基本思想:初始状态作为当前状态,选择算子对其进行操作,生成一组子状态,然后检查目标状态是否出现在这些状态中,若出现,则搜索成功;若不出现,则按照某种搜索策略从已生成的状态中再选择一个状态作为当前状态。重复上述过程。
一般搜索过程
宽度优先搜索
搜索是以接近起始节点的程度依次扩展节点的(先产生的节点先扩展)
步骤
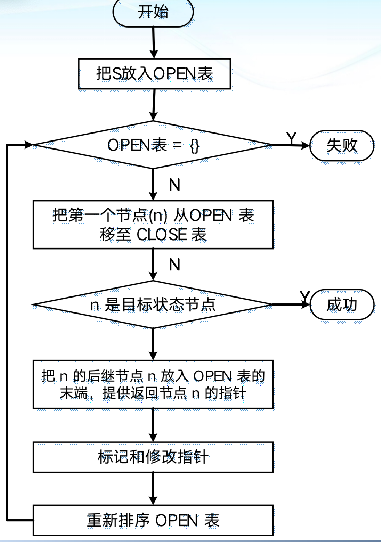
- 把初始节点 S0,放入 OPEN 表。
- 如果 OPEN 表为空。则问题无解,失败并退出。
- 把 OPEN 表中的第一个节点取出放入 CLOSE 表中,并按顺序冠以编号 n;
- 考察节点 n 是否为目标节点。若是,则求得了问题的解,成功并退出。
- 若节点 n 不可扩展,则转第 (2) 步;
- 扩展节点 n,将其子节点放到 OPEN 表的尾部,并为每一个子节点都配置指向父节点的指针,(启发式算法:并按照估值函数整体排序)然后转第 (2) 步。
- 优点
- 如果目标节点存在,用宽度优先搜索算法总可以找到该目标节点,而且是最小(即最短路径)的节点
- 缺点
- 目标节点离初始节点远的时候,搜索效率低
- 搜索深度比较大时,浪费时间
深度优先搜索
首先扩展最新产生的(最深的)节点(后产生的节点先扩展)
步骤 尾部改成首部即可
- 优点
- 需要空间少,只需保留搜索树的一部分
- 缺点
- 不是完备的(可能搜到错误的路径上,有很深/无限的搜索树,最后面找不到答案),也不算最优的
比较
- 深度优先 — 当一个问题有多个解答或多条解答路径,且只须找到其中一个时;往往应对搜索深度加以限制
- 宽度优先 — 确保搜索到最短的解答路径
共同点
优点:使用一般图搜索算法实现,简单易行
缺点:盲目搜索,效率较低
启发式搜索
利用问题所拥有的启发式信息(知识)来引导搜索,达到减少搜索范围,降低问题复杂度的目的
启发式信息:指与具体问题求解过程相关的,并可能指导搜索朝着最有希望的方向前进的控制信息。
分类:
- 陈述性启发信息
- 过程性启发信息
- 控制性信息
估值函数:用于估计节点的重要性
f(n)=g(n)+h(n)
- g(n):初始节点S0到约束节点n的实际代价
- h(n):约束节点n到目标节点Sg的最优路径估计代价 启发函数
A算法
以八皇后问题为例
ch5-搜索求解策略.pdf

