207. 课程表
210. 课程表 II
269.火星字典
public String alienOrder(String[] words) {Map<Character, Set<Character>> g = new HashMap<>();int[] indegree = new int[26];boolean isSamePrefix = buildGraph(g, indegree, words);if (isSamePrefix) return "";return bfs(g, indegree);}private boolean buildGraph(Map<Character, Set<Character>> g, int[] indegree, String[] words) {for (String word : words) for (char w : word.toCharArray()) g.putIfAbsent(w, new HashSet<>());boolean isSamePrefix = true;for (int i = 1; i < words.length; i++) {String fw = words[i - 1], sw = words[i];//前后两个相邻的单词int len = Math.min(fw.length(), sw.length());int j = 0;for (; j < len; j++) {if (fw.charAt(j) != sw.charAt(j)) {//两个单词的字符不相等char u = fw.charAt(j), v = sw.charAt(j);//u是出 v是入 u->vif (!g.get(u).contains(v)) {//图里没有的话加入,更新入度g.get(u).add(v);indegree[v - 'a']++;}isSamePrefix = false;break;//之后的已经没有比较意义了}}if (j == len && fw.length() > sw.length()) {isSamePrefix = true;return isSamePrefix;//处理["abc", "ab"]}}return isSamePrefix;}private String bfs(Map<Character, Set<Character>> g, int[] indegree) {StringBuilder sb = new StringBuilder();Queue<Character> q = new LinkedList<>();for (char c : g.keySet()) {if (indegree[c - 'a'] == 0) {q.offer(c);sb.append(c);}}while (!q.isEmpty()) {char u = q.poll();// if (g.get(u) == null || g.get(u).isEmpty()) continue;for (char v : g.get(u)) {indegree[v - 'a']--;if (indegree[v - 'a'] == 0) {q.offer(v);sb.append(v);}}}return sb.toString().length() == g.size() ? sb.toString() : "";}
444.序列重建
一些case edge case inputs:
- seqs为空 [1], [] ->
- both org and seqs 为空: [] , [[]]
- seqs 不是两个数,只有一个: [1] , [[1]]
- seqs 为空: [1] , [[],[]] ArrayIndexOutOfBoundsException or return true -> 不能用org来初始化map for edges and degree,而要用seqs来做初始化,而且在get degrees里面排除edge cases.
- edge的顺序是倒的:[1,2,3] , [[3,2],[2,1]] ->创建result,最后与org比较是否相同,不同就return false.
- edge 多于两个[4,1,5,2,6,3] , [[5,2,6,3],[4,1,5,2]]
- edge里面有invalid 的数字: [5,3,2,4,1] , [[5,3,2,4],[4,1],[1],[3],[2,4], [1000000000]] -> 在处理edge时进行判断。
方法1
public boolean sequenceReconstruction(int[] org, int[][] seqs) {
List<Integer> topoOrder = getTopoOrder(seqs);
if (topoOrder == null || topoOrder.size() != org.length) return false;
for (int i = 0; i < org.length; i++) {//比较构建的序列是否唯一
if (org[i] != topoOrder.get(i)) return false;
}
return true;
}
/**
* 收集topoOrder的序列,在之后与org一一比较
*
* @param seqs
* @return
*/
private List<Integer> getTopoOrder(int[][] seqs) {
Map<Integer, Set<Integer>> g = buildGraph(seqs);
Map<Integer, Integer> indegrees = getIndegrees(g);
List<Integer> topoOrder = new ArrayList<>();
Queue<Integer> q = new LinkedList<>();
for (Integer curr : g.keySet()) {
if (indegrees.get(curr) == 0) {//找入度为0的点
q.offer(curr);
topoOrder.add(curr);
}
}
while (!q.isEmpty()) {
if (q.size() > 1) return null;//当前的q中不止一个,说明不唯一,返回,要求graph里只有一个排列结果
Integer curr = q.poll();
for (Integer next : g.get(curr)) {
indegrees.put(next, indegrees.get(next) - 1);//弹出一个,入度-1
if (indegrees.get(next) == 0) {
q.offer(next);
topoOrder.add(next);
}
}
}
return topoOrder;
}
/**
* 构建graph
* set去重用的 4-> 5 如果出现在不同的seq中,只记录一次
* 如 [[2,4,5,7],[1,4,5,8]]这种,那么(4,5)就出现了两次
*
* @param seqs
* @return
*/
private Map<Integer, Set<Integer>> buildGraph(int[][] seqs) {
Map<Integer, Set<Integer>> g = new HashMap<>();
for (int[] edge : seqs) {//拿到每一条边
for (int i = 0; i < edge.length; i++) {
g.putIfAbsent(edge[i], new HashSet<>());
if (i == 0) continue;//i从0开始的
g.get(edge[i - 1]).add(edge[i]);//只做前后的两个数字,挨着的
}
}
return g;
}
/**
* 拿到入度
*
* @param g
* @return
*/
private Map<Integer, Integer> getIndegrees(Map<Integer, Set<Integer>> g) {
Map<Integer, Integer> indegrees = new HashMap<>();
for (Integer curr : g.keySet()) {
indegrees.putIfAbsent(curr, 0);
for (Integer next : g.get(curr)) {//遍历当前点的所有邻居节点,更新邻居节点的入度
indegrees.put(next, indegrees.getOrDefault(next, 0) + 1);
}
}
return indegrees;
}
方法二
public boolean sequenceReconstruction(int[] org, int[][] seqs) {
Map<Integer, Set<Integer>> g = new HashMap<>();
Map<Integer, Integer> indegrees = new HashMap<>();
int n = org.length;
int count = 0;
for (int[] edge : seqs) {
count += edge.length;
if (edge.length >= 1 && outArea(edge[0], 0, n)) return false;
if (edge.length == 1) {
g.putIfAbsent(edge[0], new HashSet<>());
indegrees.put(edge[0], indegrees.getOrDefault(edge[0], 0));
}
for (int i = 1; i < edge.length; i++) {
if (outArea(edge[i], 0, n)) return false;
int from = edge[i - 1], to = edge[i];
g.putIfAbsent(from, new HashSet<>());
if (g.get(from).add(to)) {
indegrees.put(to, indegrees.getOrDefault(to, 0) + 1);
}
indegrees.putIfAbsent(from, 0);
}
}
if (count < n) return false;
Queue<Integer> q = new LinkedList<>();
for (int curr : g.keySet()) {
if (indegrees.get(curr) == 0) q.offer(curr);
}
int idx = 0;
while (!q.isEmpty()) {
if (q.size() > 1) return false;
int curr = q.poll();
if (g.get(curr) == null || g.get(curr).isEmpty()) {
idx++;
continue;
}
for (int next : g.get(curr)) {
indegrees.put(next, indegrees.get(next) - 1);
if (indegrees.get(next) == 0) q.offer(next);
}
if (curr != org[idx]) return false;
idx++;
}
return idx == org.length;
}
private boolean outArea(int t, int lower, int upper) {
return t <= lower || t > upper;
}
802. 找到最终的安全状态
题解链接:图论与搜索之拓扑排序-找到最终的安全状态
理解题意
对于题干:【对于一个起始节点,如果从该节点出发,无论每一步选择沿哪条有向边行走,最后必然在有限步内到达终点,则将该起始节点称作是 安全 的。】
当一个节点,在某个环内,其是不安全的,道理也很简单,如果遇到环,该节点在环上饶了多少圈不得而知,也就无法在固定的K步能走到终点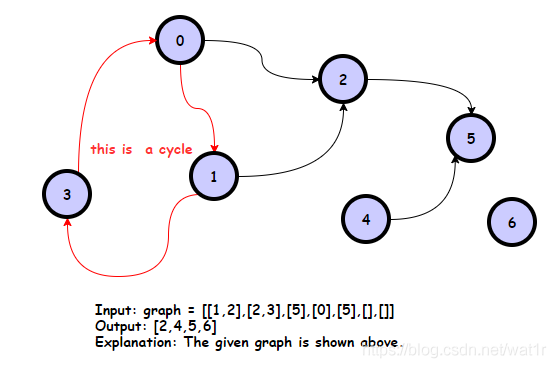
方法1:DFS+三色标记+找环
白色(用 0表示):该节点尚未被访问;
灰色(用 1表示):该节点位于递归栈中,或者在某个环上;
黑色(用 2表示):该节点搜索完毕,是一个安全节点。
public List<Integer> eventualSafeNodes(int[][] graph) {
List<Integer> res = new ArrayList<>();
int n = graph.length;
int[] color = new int[n];
for (int i = 0; i < n; i++) {
if (dfs(graph, color, i)) res.add(i);
}
return res;
}
public boolean dfs(int[][] graph, int[] color, int x) {
if (color[x] > 0) return color[x] == 2;
color[x] = 1;
for (int y : graph[x]) {
if (!dfs(graph, color, y)) return false;
}
color[x] = 2;
return true;
}
方法2:DFS+标记+找环
int[][] graph;
public List<Integer> eventualSafeNodes(int[][] graph) {
this.graph = graph;
List<Integer> res = new ArrayList<>();
int n = graph.length;
boolean[] vis = new boolean[n];
boolean[] stk = new boolean[n];
for (int i = 0; i < n; i++) {
if (!isCyclic(i, vis, stk)) res.add(i);//不是环上的,表示这个节点是安全的
}
return res;
}
private boolean isCyclic(int i, boolean[] vis, boolean[] stk) {
if (stk[i]) return true;
if (vis[i]) return false;
stk[i] = true;
vis[i] = true;
for (int x : graph[i]) {
if (isCyclic(x, vis, stk)) return true;
}
stk[i] = false;
return false;
}
方法3:拓扑排序
public List<Integer> eventualSafeNodes(int[][] graph) {
int n = graph.length;
//原图是从u->v 存的反图 v->u
List<List<Integer>> reverseGraph = new ArrayList<>();
for (int i = 0; i < n; i++) reverseGraph.add(new ArrayList<>());
int[] indegrees = new int[n];//入度数组
for (int u = 0; u < n; u++) {
for (int v : graph[u]) {
reverseGraph.get(v).add(u);
}
indegrees[u] = graph[u].length;//u节点原图的出度,即为反图u节点的入度
}
Queue<Integer> q = new LinkedList<>();
for (int u = 0; u < n; u++) {
if (indegrees[u] == 0) q.offer(u);//将入度为0的节点加入到队列中,该节点是「安全点」
}
while (!q.isEmpty()) {
int v = q.poll();
for (int u : reverseGraph.get(v)) {//开始遍历q
if (--indegrees[u] == 0) q.offer(u);
}
}
List<Integer> res = new ArrayList<>();
for (int u = 0; u < n; u++) {//入度为0的点为「安全点」
if (indegrees[u] == 0) res.add(u);
}
return res;
}
1743. 从相邻元素对还原数组
方法1:类拓扑排序
public int[] restoreArray(int[][] edges) {
int n = edges.length;
Map<Integer, Set<Integer>> g = new HashMap<>();//构建graph,做无向图
for (int[] edge : edges) {
int u = edge[0], v = edge[1];
g.putIfAbsent(u, new HashSet<>());
g.putIfAbsent(v, new HashSet<>());
g.get(u).add(v);
g.get(v).add(u);
}
Set<Integer> vis = new HashSet<>();//控制元素重复访问的set
int start = 0;//处理当前的点
int[] ans = new int[n + 1];//结果数组
int idx = 0;
for (Integer curr : g.keySet()) {
if (g.get(curr).size() == 1) {//找一个size为1的
start = curr;
vis.add(start);
ans[idx++] = start;
break;
}
}
while (vis.size() < n + 1) {
for (int next : g.get(start)) {//遍历当前点的邻居节点
if (!vis.contains(next)) {
vis.add(next);
ans[idx++] = next;
start = next;
break;
}
}
}
return ans;
}
329. 矩阵中的最长递增路径
方法1:拓扑排序
int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
int R, C;
public int longestIncreasingPath(int[][] matrix) {
R = matrix.length;
C = matrix[0].length;
int[][] outdegrees = new int[R][C];
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
for (int[] d : dirs) {
int nr = r + d[0], nc = c + d[1];
if (!inArea(nr, nc)) continue;//顺着方向找出度
if (matrix[r][c] < matrix[nr][nc]) outdegrees[r][c]++;
}
}
}
Queue<int[]> q = new LinkedList<>();
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
if (outdegrees[r][c] == 0) q.offer(new int[]{r, c});
}
}
int ans = 0;
while (!q.isEmpty()) {
ans++;
int size = q.size();
for (int i = 0; i < size; i++) {
int[] curr = q.poll();
int r = curr[0], c = curr[1];
for (int[] d : dirs) {
int nr = r + d[0], nc = c + d[1];
if (!inArea(nr, nc)) continue;
if (matrix[nr][nc] < matrix[r][c]) {//逆着方向找
outdegrees[nr][nc]--;
if (outdegrees[nr][nc] == 0) q.offer(new int[]{nr, nc});
}
}
}
}
return ans;
}
private boolean inArea(int r, int c) {
return r >= 0 && r < R && c >= 0 && c < C;
}
方法2:记忆化DFS
int[][] memo;
int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
int m, n;
public int longestIncreasingPath(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
m = matrix.length;
n = matrix[0].length;
memo = new int[m][n];
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
res = Math.max(res, dfs(matrix, i, j));
PrintUtils.printMatrix(memo);
}
}
return res;
}
private int dfs(int[][] matrix, int i, int j) {
if (memo[i][j] != 0) return memo[i][j];
memo[i][j] += 1;
for (int[] dir : directions) {
int nextI = i + dir[0], nextJ = j + dir[1];
if (inArea(nextI, nextJ) && matrix[i][j] < matrix[nextI][nextJ]) {
memo[i][j] = Math.max(memo[i][j], dfs(matrix, nextI, nextJ) + 1);
}
}
return memo[i][j];
}
private boolean inArea(int i, int j) {
return i >= 0 && i < m && j >= 0 && j < n;
}
1203. 项目管理
方法1
public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
List<List<Integer>> groupItem = new ArrayList<>();
for (int i = 0; i < (n + m); i++) groupItem.add(new ArrayList<>());
//组间与组内的依赖图
List<List<Integer>> groupGraph = new ArrayList<>();
for (int i = 0; i < (n + m); i++) groupGraph.add(new ArrayList<>());
List<List<Integer>> itemGraph = new ArrayList<>();
for (int i = 0; i < n; i++) itemGraph.add(new ArrayList<>());
//组间与组内的入度数组
int[] groupDegree = new int[n + m];
int[] itemDegree = new int[n];
List<Integer> id = new ArrayList<>();
for (int i = 0; i < n + m; i++) id.add(i);
int leftId = m;
//给未分配的item分配一个groupId
for (int i = 0; i < n; i++) {
if (group[i] == -1) {
group[i] = leftId++;
}
groupItem.get(group[i]).add(i);
}
//依赖关系图
for (int i = 0; i < n; i++) {
int currGroupId = group[i];
for (int item : beforeItems.get(i)) {
int beforeGroupId = group[item];
if (beforeGroupId == currGroupId) {
itemDegree[i] += 1;
itemGraph.get(item).add(i);
} else {
groupDegree[currGroupId] += 1;
groupGraph.get(beforeGroupId).add(currGroupId);
}
}
}
//组间拓扑关系排序
List<Integer> groupTopSort = topSort(groupDegree, groupGraph, id);
// for(int item : groupTopSort){
// System.out.printf("%d ",item );
// }
if (groupTopSort.size() == 0) return new int[0];
int[] ans = new int[n];
int index = 0;
for (int currGroupId : groupTopSort) {
int size = groupItem.get(currGroupId).size();
if (size == 0) continue;
List<Integer> res = topSort(itemDegree, itemGraph, groupItem.get(currGroupId));
if (res.size() == 0) return new int[0];
for (int item : res) ans[index++] = item;
}
// for(int item : ans){
// System.out.printf("%d ",item );
// }
return ans;
}
private List<Integer> topSort(int[] degree, List<List<Integer>> graph, List<Integer> items) {
Queue<Integer> queue = new LinkedList<>();
for (int item : items) {
if (degree[item] == 0) queue.offer(item);
}
List<Integer> res = new ArrayList<>();
while (!queue.isEmpty()) {
int u = queue.poll();
res.add(u);
for (int v : graph.get(u)) {
if (--degree[v] == 0) queue.offer(v);
}
}
for(int item : res){
System.out.printf("%d ",item );
}
return res.size() == items.size() ? res : new ArrayList<>();
}

