归并排序
归并排序本身是一个递归的过程,在每一次递归的过程中,将数组分成等长的2部分,然后左边进行递归,然后右边跟着递归,然后进行一个排序,这个排序的过程的前提是左右部分都是有序的,然后左右两边的数据分别从头部进行比较,小的数就存入一个新的数组中,并且相应的位置后退一步,这样下来可以使左右两边的数据全部有序的进入,当有一边的数已经全部进入数组,那么直接把剩下的那边依次放入数组就完成了。
public class mergesort {/** 如何进行归并排序?* 1.首先传入一个数组,然后我们把他分开2分,然后这2分进行递归,递归到结束的条件就是我们分开后的2分中只有* 一个元素,然后让这两个元素进行排序,排序的过程是两边的数从头开始比较,并且开辟一个新的数组,小的数先进数组,大的数后进入,* 当一侧的数据读完后,就将剩余那部分的数全部放入数组,然后在将排好序的数,重新放回最初传进来的数组,一层层递归结束后,就是* 排好顺序的数了** *///1.先判断这个数组是否为空或者只有一个元素//解释一下为什么没有返回值,因为传入的参数是一个数组,我们在排序中会对数组中的//元素进行排序,所以说传入后,即使不返回,数组也变了static void mergesort(int[] arr){if (arr==null||arr.length<=1){return ;}mergesort(arr,0,arr.length-1);}//如果不为空就进入正式开始的递归排序,这里传入的参数,第一个是数组,第二个是开始位置,第三个是结束位置static void mergesort(int[] arr,int start ,int end){//先声明递归结束的条件if (start==end){return ;}//如果不是就2分,先找到中间点int mid = (start+end)/2;//那么分开的部分进行递归的开始和结束位置分别是start mid 和 min+1 endmergesort(arr, start, mid);mergesort(arr,mid+1,end);//关键在于这个merge,这个merge要怎么写?merge(arr,start,mid,end);}static void merge(int[] arr,int start,int mid,int end){//传进来了三个参数,然后依次进行归并排序//首先要有2个指针,分别指向2边的开头,然后比较结束的条件就是任意一方的数读到边界!int[] newarray = new int[arr.length];int i = start;int p1 = start;int p2 = mid+1;while((p1<mid+1)&&(p2<end+1)){//这句话的意思就是两边指针所指向的位置进行比较,如果//小的一边对数组进行赋值,指针向后移动一位newarray[i++] = arr[p1]<arr[p2]?arr[p1++]:arr[p2++];}while(p1<mid+1){newarray[i++] = arr[p1++];}while(p2<end+1){newarray[i++] = arr[p2++];}//拷贝回去for(int j = start;j<=end;j++){arr[j] = newarray[j];}}public static void main(String[] args) {int[] arr = new int[]{2,5,4,1};mergesort(arr);for (int i : arr) {System.out.println(i);}}}
问题拓展,小和问题,求逆序对
记不住了!
快速排序
荷兰国旗问题!
什么是荷兰国旗问题?首先我们先看荷兰国旗
由三种颜色组成,所以我们今天要研究的就是给定一个数组,和一个数num,对数组进行排序,把大于在这个数的数放在右边,小于这个数的数放在数组左边,等于这个数的数放在中间,当然,在大于和小于的部分,我们不要求有序。
所以我们要思考怎么去做?(要求额外的空间复杂度是O(1)),只能用有限制的几个变量进行操作
首先划分2个边界,一个是小于边界,一个是大于边界,小于边界在数组的最左边,大于边界在数组的最右边,我们根据一下的3条规则进行操作
1.数组从左向右遍历,遇到比num小的数,我们将它与小于边界的数进行交换,然后小于边界向后移动一位,
2.当遇到等于num的数,我们的不进行任何操作,继续遍历
3.当遇到大于num的数,将大于边界所指向的数和它进行交换,然后大于边界向前移动一位。然后这次循环重新进行
终止的条件就是我们遍历的数到达了大于的边界就停止遍历。
public class NetherlandsFlag {static void partion(int[] array,int a,int b,int nums){int left = a;int right= b;int i = a;//确定左右边界,可以直接却认为数组的开头和结尾(长度减一)while (i<=right) {//只要没有到达最大数的边界就一直遍历下去,3种条件//1.比num小if (array[i]<nums){//进行交换操作,交换的对象,当前数和小于边界所指向的数,执行结束后i++,left++int temp = array[i];array[i] = array[left];array[left] = temp;i++;left++;}//等于numelse if(array[i]==nums){i++;}//大于numselse{int temp = array[i];array[i] = array[right];array[right] = temp;right--;}}}public static void main(String[] args) {int[] array = new int[]{0,7,8,5,5,9,5,4,5,3};partion(array,0,array.length-1,5);for (int i : array) {System.out.println(i);}}}
快速排序
快速排序就是以荷兰国旗排序为基础,这次只给一个数组,我们进行排序,那么参照荷兰国旗,我们可以首先选取数组最后一个数作为num,然后对数组中的数进行排序,分为,小于,等于,大于三部分,排序之后我们将大于区域的最前面的数和num的位置进行交换,然后以num的左右边界的最后一个数作为nums,进行新一轮的排序,这样递归下来我们最终就可以确定出所有数的正确顺序,每次确定一个数。
public class NetherlandsFlag {static int[] partion(int[] array,int a,int b,int nums){int left = a;int right= b;int i = a;//确定左右边界,可以直接却认为数组的开头和结尾(长度减一)while (i<=right) {//只要没有到达最大数的边界就一直遍历下去,3种条件//1.比num小if (array[i]<nums){//进行交换操作,交换的对象,当前数和小于边界所指向的数,执行结束后i++,left++int temp = array[i];array[i] = array[left];array[left] = temp;i++;left++;}//等于numelse if(array[i]==nums){i++;}//大于numselse{int temp = array[i];array[i] = array[right];array[right] = temp;right--;}}//这里的right永远指向的是下一个未知的数,所以返回最后一个确定的最大值的位置,那么就返回right-1,左边的就是left-1return new int[]{left-1,right+1};}static void quicksort(int[] arr,int start,int end){//最初传递的数组肯定是从0到末尾,首先确定出末尾位置int num = arr[end];//然后剩下的部分进行排序,传入数组的起点,重点 和 numint[] res = partion(arr, start, end - 1, num);//拿到交换的位置int temp = arr[end];arr[end] = arr[res[1]];arr[res[1]] = temp;//交换完毕,递归左右两边,右边的起点是partion+1 ,左边的起点没返回,if (res[0]>=start){quicksort(arr,start,res[0]);}if (res[1]<end){quicksort(arr,res[1]+1,end);}}public static void main(String[] args) {int[] array = new int[]{0,7,8,5,5,9,5,4,5,3};quicksort(array,0,array.length-1);for (int i : array) {System.out.println(i);}}}
堆排序
package com.zjl.heap;import java.lang.Math;public class heap {//堆排序static void heapsort(int[] arr){//首先建堆heapinsert(arr);//不断的调整;for (int i = arr.length-1;i>0;i--){heapify(arr,0,i);}}//建立一个堆static void heapinsert(int[] arr){/*怎么建立,传入一个数组,有一个表示当前堆大小的指针* 每次我们读取一个数,然后调整一下看是否满足堆的定义,然后指针后移*///判断是否满足堆。判断之后要继续数组数据for(int i = 0;i<arr.length;i++){int heapsize = i;while(arr[heapsize]>arr[(heapsize-1)/2]){//进行交换int temp = arr[heapsize];arr[heapsize] = arr[(heapsize-1)/2];arr[(heapsize-1)/2] = temp;//交换位置之后,继续判断,heapsize改变,这里要用另一个指针;heapsize = (heapsize-1)/2;}}}//堆化,首先我们的本质思想是拿走最顶上得数,用最后一个数替代,比如说已经建好的堆在这块static void heapify(int[] arr, int position, int heapsize){int size = heapsize;//本质就是堆顶和堆最后一个进行交换;int temp = arr[position];arr[position] = arr[size];arr[size] = temp;int i = position;//代表我们已经把最大数的一部分给掩盖住了//然后堆化,遵从3条规则 1.这个位置先判断有没有左右孩子,没有就算了,//有的话找出左右孩子中的较大的一// 个,2.和当前的结点进行比较,当前大不动,不然就交换//,然后从交换位置再次开始这次操作;while((2*i+1)<size){//代表一定有左孩子int max = arr[2*i+1];int index = 2*i+1;//判断有没有右孩子if ((2*i+2)<size){max = Math.max(arr[2*i+1],arr[2*i+2]);index = arr[2*i+1]>arr[2*i+2]?2*i+1:2*i+2;}//然后和父节点比较if (arr[i]<max){//这里要进行交换,但是没有索引;temp = arr[i];arr[i] = arr[index];arr[index] = temp;i = index;}//否则这就是这个位置应该放置的元素;else{break;}}}public static void main(String[] args) {int[] arr = new int[]{5,2,1,3};heapsort(arr);for (int i : arr) {System.out.println(i);}}}
链表汇总
基础常识
链表是一种逻辑上连续的数据结构,我们只能通过当前结点找到下一个结点,不能像数组一样快速的听过下标找到指定的位置。所有链表具有增删快,查找慢的特点。
五道题
这里将汇总在LeetBook上出现的几个比较经典的链表题目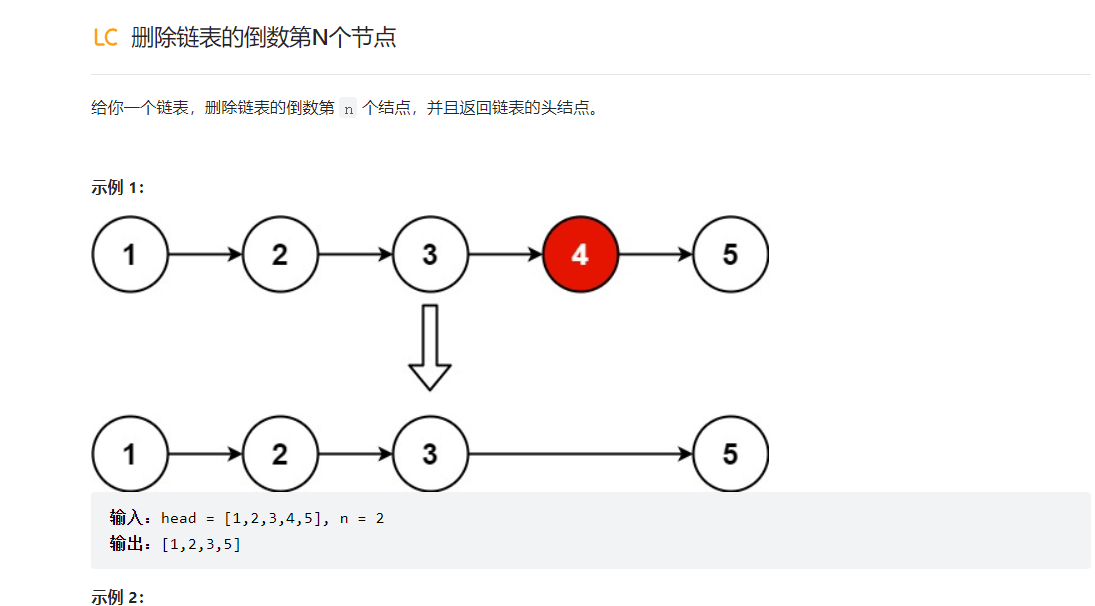
这道题就很有趣,因为链表是没有下标的,所以我们在遍历的时候,是不知道链表的长度的,或者说只有走一遍才能知道到底有多少个Node,然后再次遍历得出所找的结点。当然这样做是不够快的,应该追求一次遍历就出结果,我们这里就要提一提双指针的问题了;所谓双指针,就是在刚开始有2个指针都指向链表的头部,然后我们可以让其中一个先走几步,然后再让第二个和第一个一起走,这样当第一个走到终点的时候,第二个指针就会距终点一定的距离,这个距离就是我们第一个指针先走出来的长度,所以如果说,我们求倒数第一个,那就先走一步,到最后我们的慢指针就会指向倒数第一个的前一个位置,然后进行p.next = p.next.next;操作进行删除即可;这就是大致思路,但是这个问题还是有细节需要我们注意的;
1.如果只有一个结点,并且删除第一个,而且p.next = p.next.next;这句话也会报错。(会很难处理,产生空指针异常)所以说为了解决这个问题,我们可以引出一个新的链表头,把head这个头结点在前置一个结点,然后快慢指针都从这个位置出发,我们就可以按照这个思路快速的解决问题了;
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public ListNode removeNthFromEnd(ListNode head, int n) {ListNode p = new ListNode();//这是在头结点前面又加了一个结点,用于作为快慢两个指针的出发点;p.next = head;ListNode slow = p;ListNode fast = p;//先走出几步来;while(n>0){fast = fast.next;n--;}//走到终点,走到重点的标志就是最后一个结点;while(fast.next!=null){fast = fast.next;slow = slow.next;}//删除slow.next = slow.next.next;//因为这个引入的头结点是不会进行任何删除的操作,所以返回他的下一个就行了;return p.next;}}
总结这个题做起来还是比较模糊的,前置一个结点的思想掌握的还是不够好;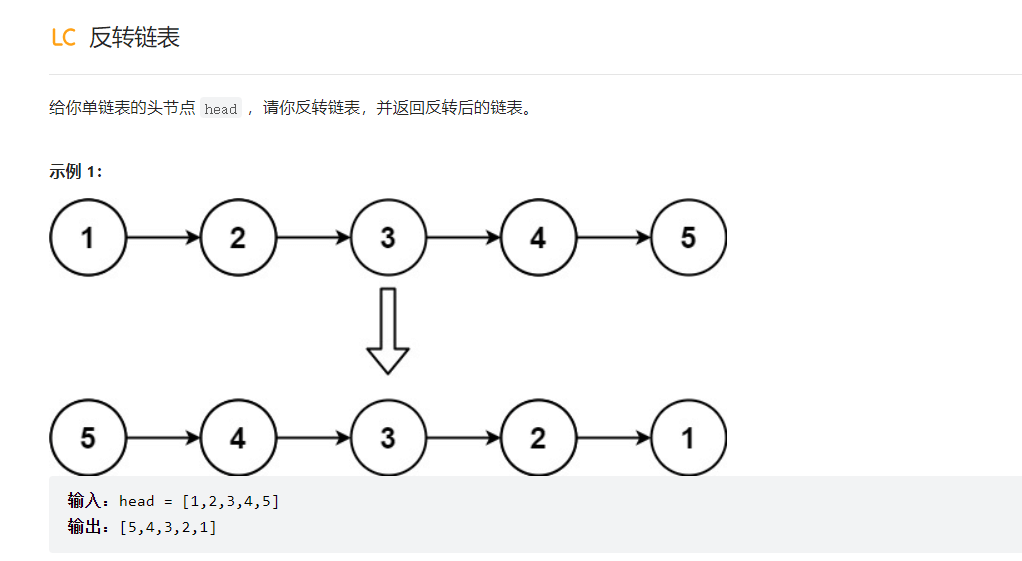
这是最基本的一道链表反转的题考的就是怎么把这个链表反转过来,也就不说什么迭代,递归之类的,我就用我自己的方法,这方法也不是很弱鸡,先看代码:
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public ListNode reverseList(ListNode head) {if( head==null || head.next==null){return head;}ListNode p = head.next;head.next = null;while(p!=null){ListNode v = p.next;p.next = head;head = p;p = v;}return head;}}
代码解读:首先对于进入的链表进行判断,如果说只有一个结点,或者本身就是空,直接返回就可以了,这里要注意判断的顺序,先判断是不是 null ,再判断有没有next 。然后我们用一个p指针指向当前链表head 的下一个结点,然后因为当前是第一个Node ,所以把他next ,指向空,然后就可以进入循环了,循环结束的标志,那一定是到了链表的尾部,那也就是p!=null,持续循环。在循环体中,我们再用一个指针指向p的next ,这样保证p逆转的时候不会丢失剩下的链表,逆转结束后,我们试想写一部要进行操作的对象中,如今的p就是当年的head ,如今的v就是当年的p,于是交换值,再次循环,知道p是空,代表全部逆转完毕,刚好返回head 就完成了任务;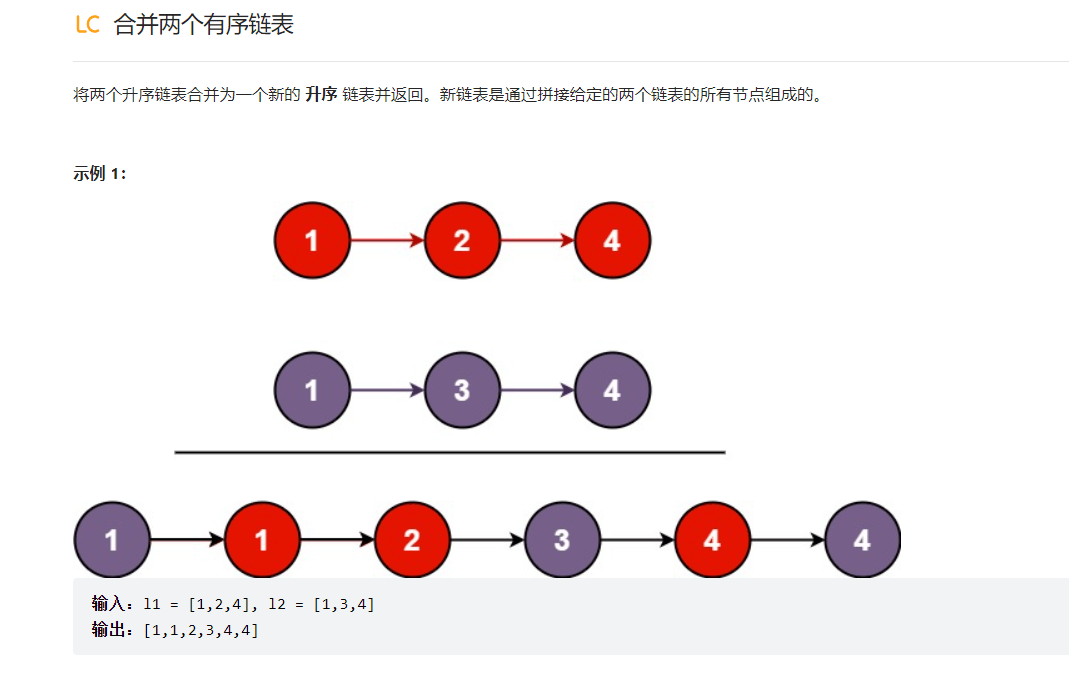
简单来看就是归并排序罢了,但是我们没有数组来承接它,所以要改,就把整条链表打乱,定义一个新的头结点,对这两条字符串进行串串,也就是merge过程,这里就不过BB,看代码就好
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public ListNode mergeTwoLists(ListNode list1, ListNode list2) {ListNode p = new ListNode();ListNode p3 = p;ListNode p1= list1;ListNode p2= list2;while(p1!=null&&p2!=null){if(p1.val<p2.val){p.next = p1;p = p.next;p1 = p1.next;}else{p.next = p2;p = p.next;p2 = p2.next;}}while(p1!=null){p.next = p1;p = p.next;p1 = p1.next;}while(p2!=null){p.next = p2;p = p.next;p2 = p2.next;}return p3.next;}}
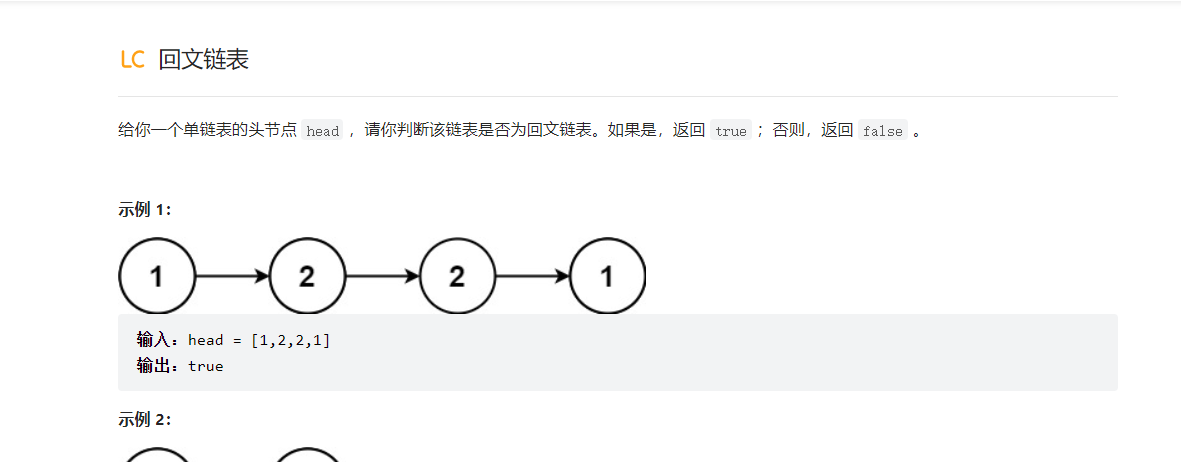
这道题的最优解就是利用快慢指针一个走到头,另一个走到中间,然后将中间的结点后面的部分进行逆转,且中间只向空,得到两条链表进行比较得出是否为回文,主要知识点就2个,一个是快慢指针,另一个是反转;
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public boolean isPalindrome(ListNode head) {//首先定义一个快慢指针,走到最后,快指针指向末尾,满指针直到中间位置;ListNode fast = head;ListNode slow = head;while(fast.next!=null){fast = fast.next;if(fast.next == null){break;}fast = fast.next;slow = slow.next;}//这样走完,我们把满指针指向null;ListNode head2 = reversal(slow.next);slow.next = null;while(head!=null && head2!=null){if(head.val!=head2.val){return false;}head = head.next;head2 = head2.next;}return true;}public static ListNode reversal(ListNode head){if(head==null || head.next== null){return head;}ListNode p = head.next;head.next = null;while(p!=null){ListNode v = p.next;p.next = head;head = p;p = v;}return head;}}
最后一道,就是扣圈问题,可以走到null,自然不是环,走不到null,迟早会出现二者相等的时刻;
二叉树
package com.zjl;import java.util.ArrayList;import java.util.Stack;/*** @Author 朱金龙* @Date* @Version 1.0*/public class Binary_tree {//这里主要要进行总结的知识点一共有3个,分别是 树的非递归三种遍历方式 ,树的广度搜索,以及返回最大的宽度//这是前序遍历方式static void PreOrderTraversa(ListNode head){//前序遍历的方式是中前后,非递归的实现方式:1.head 入栈 ,然后进入循环,循环结束的条件是,栈为空,// 每次进行的操作就是弹出栈顶,然后压入弹出栈顶的元素的右左结点,如果没有就算了Stack<ListNode> list = new Stack<>();list.push(head);//定义一个cur指针指向我们的head ,后面是会进行动态的变化的while (!list.empty()){ListNode cur = list.pop();System.out.println(cur.value);if (cur.right!=null){list.push(cur.right);}if (cur.left!=null){list.push(cur.left);}}}//后序的遍历方式是前序的改良版, 前序的顺序 是中左右 ,这里我们入栈的顺序是中右左,// 改成中 左 右 之后 ,1.弹栈的顺序是 中 右 左 2. 另一边入栈的顺序就是 左 右 中// 放入一个栈中,然后在倒着取出就是后序的顺序了;static void PostOrderTraversal(ListNode head){Stack<ListNode> list = new Stack();Stack<ListNode> res = new Stack();list.push(head);while (!list.empty()){ListNode cur = list.pop();res.push(cur);if (cur.left!=null){list.push(cur.left);}if (cur.right!=null){list.push(cur.right);}}//遍历输出栈while(!res.empty()){System.out.println(res.pop().value);}}//中序遍历的方式 , 还是栈,用栈来模拟这个递归//首先我们 从根结点进行遍历的子节点,入栈,然后进行pop ,pop 的过程中,检查是否有右结点,如果有右结点,//就以右结点为根,再次进行遍历入栈;static void InorderTraversal(ListNode head){Stack<ListNode> list = new Stack<>();//左结点全部入栈;while (head!=null){list.push(head);head = head.left;}while(!list.empty()){ListNode cur = list.pop();System.out.println(cur.value);if (cur.right!=null){head = cur.right;//如果不是空的,就怎么处理?while (head!=null){list.push(head);head = head.left;}}}}public static void main(String[] args) {ListNode listNode1 = new ListNode(1);ListNode listNode2 = new ListNode(2);ListNode listNode3 = new ListNode(3);ListNode listNode4 = new ListNode(4);ListNode listNode5 = new ListNode(5);ListNode listNode6 = new ListNode(6);ListNode listNode7 = new ListNode(7);ListNode listNode8 = new ListNode(8);listNode1.left = listNode2;listNode2.left = listNode4;listNode2.right = listNode5;listNode1.right = listNode3;listNode3.left = listNode6;listNode3.right = listNode7;listNode7.right = listNode8;InorderTraversal(listNode1);// PreOrderTraversa(listNode1);ArrayList arrayList = new ArrayList();arrayList.add(0);}}class ListNode {int value;ListNode left;ListNode right;public ListNode(int value){this.value = value;}}
static void WidthSearch(ListNode root){//如果要统计最大宽度的话//统计每一层的数值//这还能当栈用啊?ArrayList<List<Integer>> lists = new ArrayList<>();LinkedList<ListNode> list = new LinkedList<>();//入队list.add(root);//开始进行pop和push操作while(!list.isEmpty()){//代表当前层的结点数int currsize = list.size();ArrayList<Integer> curvals = new ArrayList<>();//循环这一层for (int i = 0; i < currsize; i++) {//弹出队列ListNode cur = list.remove();//可以装进当前这层的集合;curvals.add(cur.value);if (cur.left!=null){list.add(cur.left);}if (cur.right!=null){list.add(cur.right);}}//读完装进大的集合;lists.add(curvals);}}
二叉树的递归
二叉树的递归一共有2种,一种是自上而下的递归,另一种是自下而上的递归方式
两种方式主要不同在于我们看问题的角度不同,
自上而下的方式,是从树的root出发,首先根节点会给子节点一个值,然后子节点接受到值后,会和root结点做同样的操作,把自己的值和root传进来的值分配给左右子结点,知道,左右子结点不能在传递,即到达叶子结点的时候,我们停止递归,然后从下向上一层一层的筛选传递会来的左右结点的值,知道传递到root停止上传。
自下而上的方式,是属于程序从root开始,但是不会传递一个初始值下去,而是开始就进行层层递归,然后等待到达叶子结点后,由叶子结点将数值进行返回,然后将每个叶子结点的返回值进行层层加工,然后筛选出是左还是右边的结点,进行返回。
所以说,往往我们第一种方式的叶子结点返回的值是很大的,是层层积累下来的 ,第二种方式就是较小的,因为每一层的计算方式已经写好了,就等着子节点传回数值进行计算了;
然后,其实两种递归的代码结构都很简单
1.首先把我们的root结点想象成叶子结点,对它写出临界条件和返回值2.无脑的进行递归,然后定义两个变量用来收集我们需要的值3.进行上一层的返回,这个返回中要对左右两个返回值进行判断,根据判断结果,来看我们要返回的是哪一个值补充:往往复杂的问题,并不会让我们递归到叶子结点才进行返回,往往需要我们分析一下特殊情况,当然这些特殊情况直接堆到第一层结构中大多数都是可以解决的;
前缀树
class Trie {//难道不是只有一个root 就行来了吗;Node root;//前缀树的数据结构class Node{int pass;//记录走过的次数int end;//记录多少单词以他结尾Node[] nodes ;//26个空间代表着我们的26个可以进行连接的字母;public Node(){//在这里进行初始化;nodes = new Node[26];}}public Trie() {//怎么进行初始化???root = new Node();}public void insert(String word) {//传入一个字符串,然后把他放到树中,先转换成字符数组word.length();char[] str = word.toCharArray();// root结点是不会方数字的,但是要一个指针沿着它走下去Node p = root;p.pass++;for (int i = 0; i < str.length; i++) {//读取数组的每一个字符,然后找对应的数组的位置int index = str[i] - 'a';//如果说我们这个node 的位置的这个数组是空的if (p.nodes[index] == null){//插入一个新的nodep.nodes[index] = new Node();}//如果说已经有了的话p = p.nodes[index];p.pass++;}p.end++;}public boolean search(String word) {char[] str = word.toCharArray();//查找操作,肯定是从头查了Node p = root;//假设传进来的是空传//进行查询for (int i = 0; i < str.length; i++) {int index = str[i] - 'a';//先判断是否存在,如果不存在就直接返回false;if (p.nodes[index] == null){return false;}//如果存在的话,就往下走;p = p.nodes[index];}//遍历完成后,判断一下有没有这个结尾的字符if (p.end==0){return false;}return true;}public boolean startsWith(String prefix) {//找前缀char[] str = prefix.toCharArray();//假设没有insert 代表这个树是完全空的,然后查nullNode p = root;for (int i = 0; i < str.length; i++) {int index = str[i] - 'a';if (p.nodes[index]==null){return false;}p = p.nodes[index];}if(p.pass<1){return false;}return true;}
贪心算法
其实没有什么技巧可以说的,就是对一件事只考虑其中的一个因素罢了

