树🌲 - 自平衡二叉搜索树 - 《数据结构与算法》

节点的高度
">
平衡因子
平衡操作 - AVL旋转
插入节点
移除节点

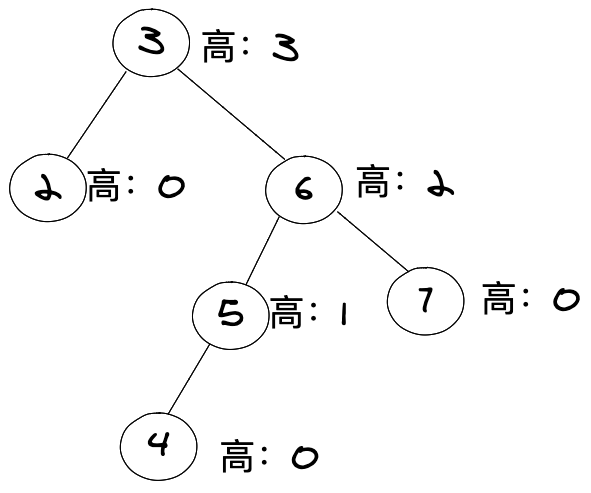
自平衡树（AVL），是为了解决二叉搜素树存在的可能某一节点会嵌套太深的缺点。ASVL是一种自平衡二叉搜索树，左子树和右子树高度最多相差1。在添加或移除节点时，AVL树会尽可能尝试转换成完全树.
在AAVL中，需要对每个节点计算右子树高度和左子树高度之间的差值，该值（hr-hl）应为0，1，-1.如果结果不是这三个值之一，需要平衡树AVL树，这就是平衡因子的概念；

节点的高度

节点的高度是从最下开始获取

最下的节点是0开始（后面总结：高度高度从0或者1开始都不影响计算）
如果有多个分之，中间的高度是按照最高的高度计算获取。

平衡因子

平衡因子只能是 0，1，-1 ，如果不是这三个值之一则就需要计算该AVL树；
平衡因子计算，有的说左高-右高，有的说右高-左高，不过不影响计算。下面按照 左高-右高计算获取平衡因子
每个节点都右自己的平衡因子 ,如下7，13也有自己平衡因子，只不过没有值所以平衡因子为0；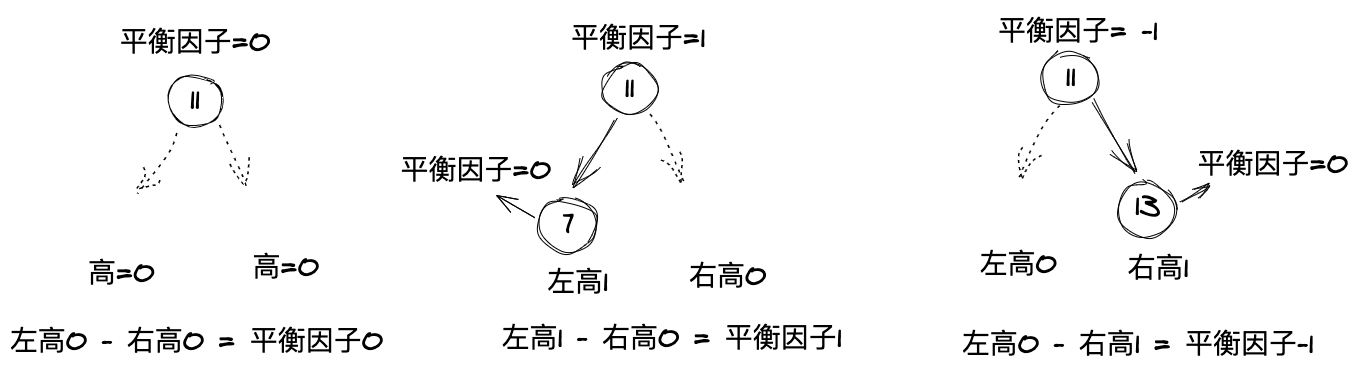

平衡操作 - AVL旋转

在对AVL树添加或移除操作后，需要计算节点的高度并验证树是否需要进行平衡。向AVL树插入如节点时，可以执行单旋转或双旋转两种平衡操作。

左-左（LL）：向右的单旋转
右-右（RR）：向左的单旋转
左-右（LR）：向右的双旋转（先LL旋转，后RR旋转）
右-左（RL）：向左的双旋转（先RR旋转，后LL旋转）
左-左（LL）：向右的单向旋转
这种情况出现于节点的左侧节点的高度大于右侧节点的高度时候。
解：因为第二层肯定比三层小，比一层大。所以直接把三层放到到二层右侧就行。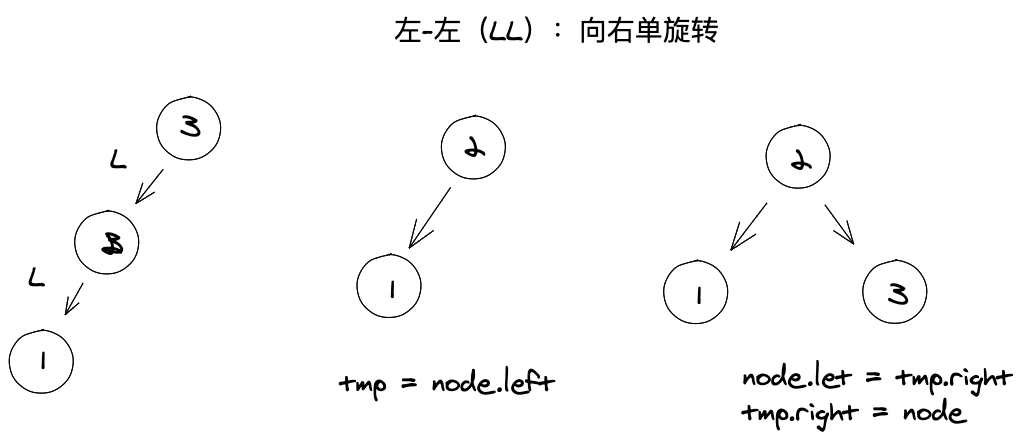
```
  // LL 向左单旋转
  rotationLL(node) {
      const tmp = node.left;
      node.left = tmp.right;
      tmp.right = node;
      return tmp
  }
```

右-右（RR）：向左的单向旋转

右侧子节点的高度大于左侧子节点的高度，并且右侧子节点也是平衡或右侧较重的。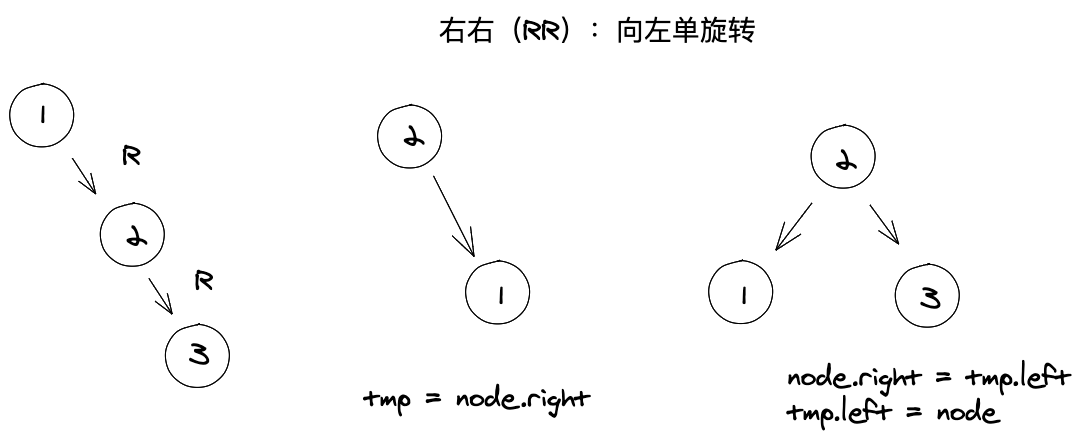

    //  RR 向右单旋转
    rotationRR(node) {
        const tmp = node.right;
        node.right = tmp.left;
        tmp.left = node;
        return tmp;
    }

左-右（LR）：先右的双旋转

左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重，这种情况对左侧子节点进行左旋转来修改，然后在对不平衡的节点来一个右旋转来修复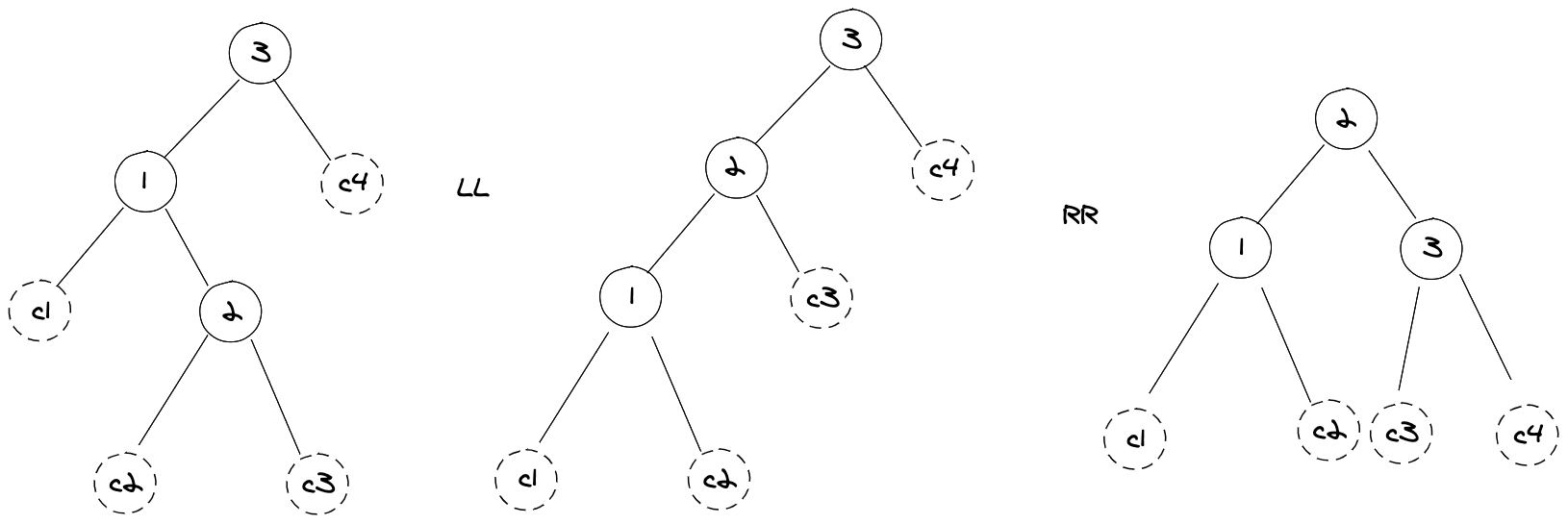

    // LR 向右的双旋转
    rotationLR(node) {
        node.left = this.rotationRR(node.left);
        return this.rotationLL(node)
    }

右-左（RL）：向左的双旋转

右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重，先进行右旋转，在通过左旋转修复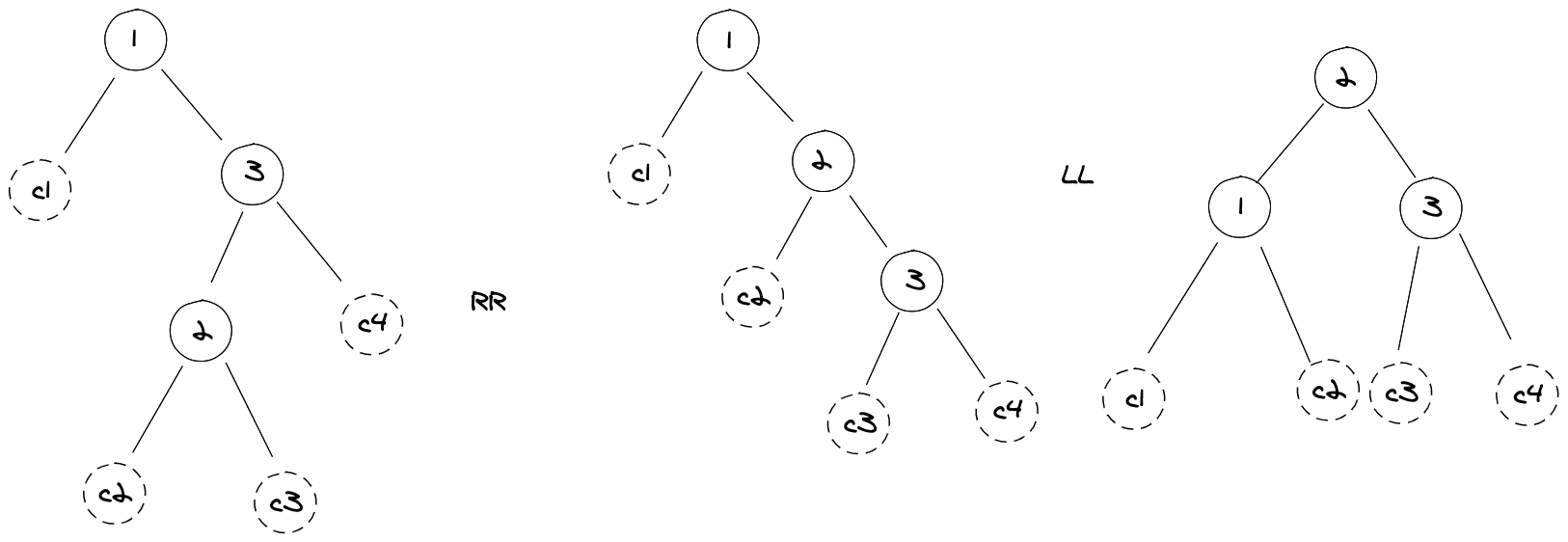

    // Rl 右左旋转
    rotationRL(node) {
        node.right = this.rotationLL(node.right);
        return this.rotationRR(node);
    }

插入节点

    insert(key) {
        this.root = this.insertNode(this.root, key);
    }
    //  插入节点 如果不在插入  存在直接返回  节点不平衡 旋转
    insertNode(node, key) {
        if (node === null) {
            //  没有数据的时候直接创建
            return new Node(key)
        } else if (this.defaultCompare(key, node.key) === -1) {
            //  插到左侧
            node.left = this.insertNode(node.left, key)
        } else if (this.defaultCompare(key, node.key) === 1) {
            //  插到右侧
            node.right = this.insertNode(node.right, key)
        } else {
            //  如果插入的节点存在 直接返回
            return node;
        }
        //  进行二叉树平衡操作
        const balanceFactor = this.getBalanceFactor(node);
        //  左侧树插入节点后不平衡情况下
        if (balanceFactor === BalanceFactor.UNBALANCED_LEFT /* 5 */) {
            //  插入值比左侧小
            if (this.defaultCompare(key, node.left.key) === -1) {
                node = this.rotationLL(node)
            } else {
                return this.rotationLR(node);
            }
        }
        //  右侧树插入节点后不平衡情况下
        if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT /* 1 */) {
            //  插入值比右侧小
            if (this.defaultCompare(key, node.right.key) === 1) {
                debugger
                node = this.rotationRR(node);
            } else {
                return this.rotationRL(node)
            }
        }
        return node;
    }

移除节点

    remove(key){
        return this.removeNode(this.root,key)
    }
    //  移除节点
    removeNode(node, key) {
        //  使用继承方法的移除；    递归移除
        node = super.removeNode(node, key);
        if (node === null) return node //    null 不需要平衡
        //  检测树是否平衡  递归计算 以移除的节点 为根节点的平衡因子
        const balanceFactor = this.getBalanceFactor(node);
        //  左侧移除完后不平衡
        if (balanceFactor === BalanceFactor.UNBALANCED_LEFT /* 5 */) {
            //  计算左侧树平衡因子
            const balanceFactorLeft = this.getBalanceFactor(node.left);
            //  左侧树先左不平衡
            if (
                balanceFactorLeft === BalanceFactor.BALANCED || //  3
                balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT    //  4
            ) {
                //  左侧旋转
                return this.rotationLL(node)
            }
            //  左侧树向右不平衡
            if (balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT/* 2 */) {
                //  旋转
                return this.rotationLR(node);
            }
        }
        //  右侧树移除完后不平衡
        if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT/* 1 */) {
            //  计算右侧平衡因子
            const balanceFactorRight = this.getBalanceFactor(node.right);
            // 右侧树向右不平衡
            if (
                balanceFactorRight === BalanceFactor.BALANCED ||    //  3
                balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT  //  2
            ) {
                //  有侧旋转
                return this.rotationRR(node)
            }
            //  右侧向左不平衡
            if (balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT/* 4 */) {
                // 左右旋转
                return this.rotationRL(node.right)
            }
        }
        return node;
    }

https://github.com/qdwds/data-structure

自平衡二叉搜索树