本周我们继续来阅读 Go 语言中 sort 包的源码，这次我们把注意力放在 quickSort（快速排序） 与 heapSort（堆排序）上，看看两者实现的原理与区别，下面让我们先从 quickSort（快速排序）开始。

QuickSort

为了更好的理解 Go 源码中的 quickSort 逻辑，我们先来了解一下正常或者说是一般的 quickSort 逻辑。quickSort 又称 partition-exchange sort（分区交换排序），如图 1 所示，quickSort 的核心思想是在数据中选出一个基准值 pivot，然后使用分治法，把数据分为大小两个区，达到局部有序，然后递归分区，直到整体有序。

图片.png
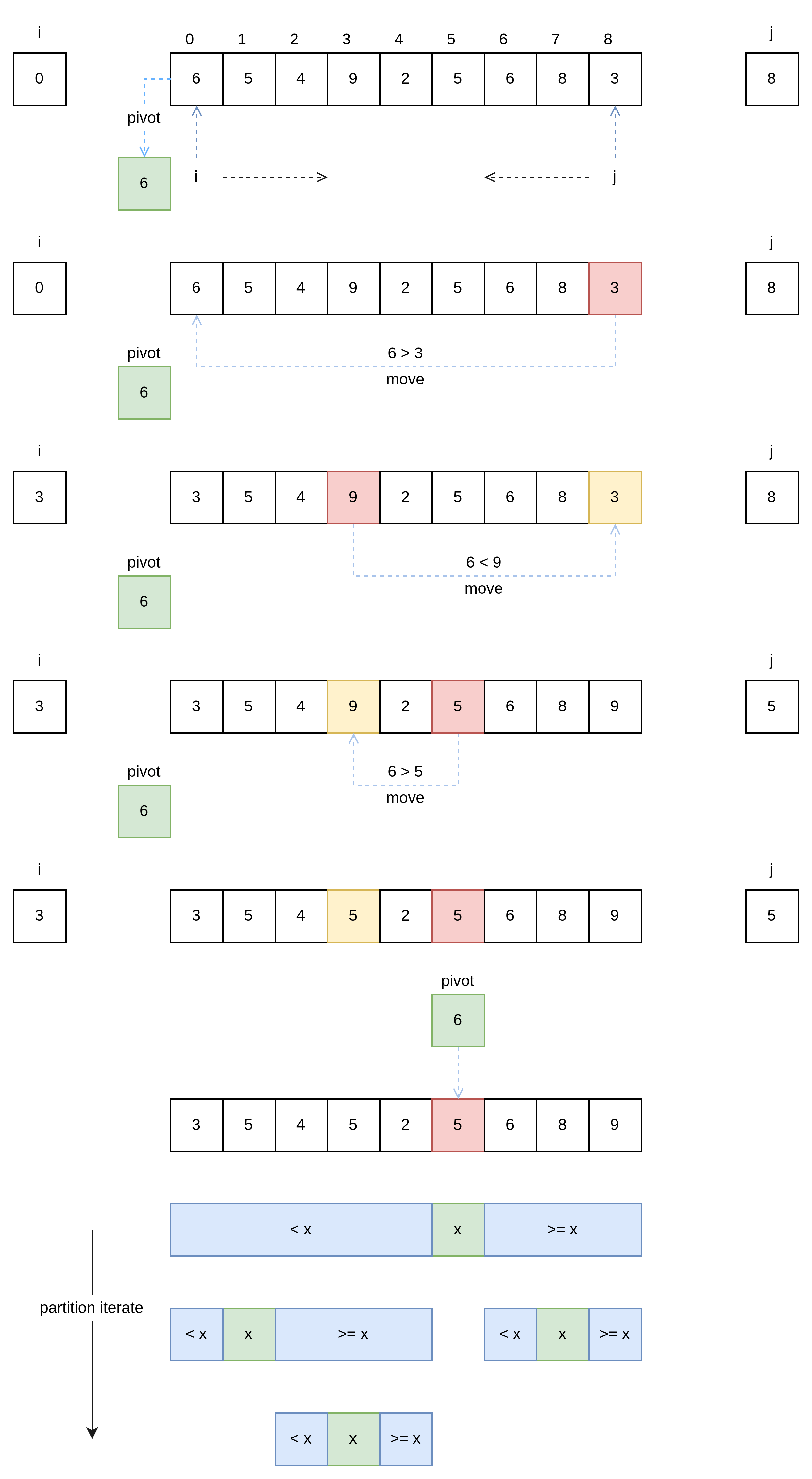
接下来看源码中的实现，以下源码中 L9 ～ L19 为快速排序逻辑部分，maxDepth 方法作为切换到 heapSort 的条件，传入数据长度 n，依据快速排序的分治逻辑计算最大迭代深度，接着来到 L9 有一个 doPivot 方法，看名字这个方法的功能应该是从数据中选出一个 pivot 基准值，而且代码其它部分并无分区逻辑，所以推测 doPivot 方法全部的作用为选取基准值，然后根据基准值对数据进行分区，最后返回 pivot 用于下一次迭代，但是 doPivot 返回了两个值， mlo 与 mhi，看样子是一个最小值和一个最大值，并不知道具体作用，继续往下看，L13 像是两个“长度”的比较，L14 ～ L18 总是对较小的进行排序，接下来我们带着疑问继续看 doPivot 方法。 

  1. // ...
  3. func quickSort(data Interface, a, b, maxDepth int) {
  4.     for b-a > 12 { // Use ShellSort for slices <= 12 elements
  5.         if maxDepth == 0 {
  6.             heapSort(data, a, b)
  7.             return
  8.         }
  9.         maxDepth--
  10.         mlo, mhi := doPivot(data, a, b)
  11.         // Avoiding recursion on the larger subproblem guarantees
  12.         // a stack depth of at most lg(b-a).
  13.         if mlo-a < b-mhi {
  14.             quickSort(data, a, mlo, maxDepth)
  15.             a = mhi // i.e., quickSort(data, mhi, b)
  16.         } else {
  17.             quickSort(data, mhi, b, maxDepth)
  18.             b = mlo // i.e., quickSort(data, a, mlo)
  19.         }
  20.     }
  21.     if b-a > 1 {
  22.         // Do ShellSort pass with gap 6
  23.         // It could be written in this simplified form cause b-a <= 12
  24.         for i := a + 6; i < b; i++ {
  25.             if data.Less(i, i-6) {
  26.                 data.Swap(i, i-6)
  27.             }
  28.         }
  29.         insertionSort(data, a, b)
  30.     }
  31. }
  33. //...
  35. // maxDepth returns a threshold at which quicksort should switch
  36. // to heapsort. It returns 2*ceil(lg(n+1)).
  37. func maxDepth(n int) int {
  38.     var depth int
  39.     for i := n; i > 0; i >>= 1 {
  40.         depth++
  41.     }
  42.     return depth * 2
  43. }

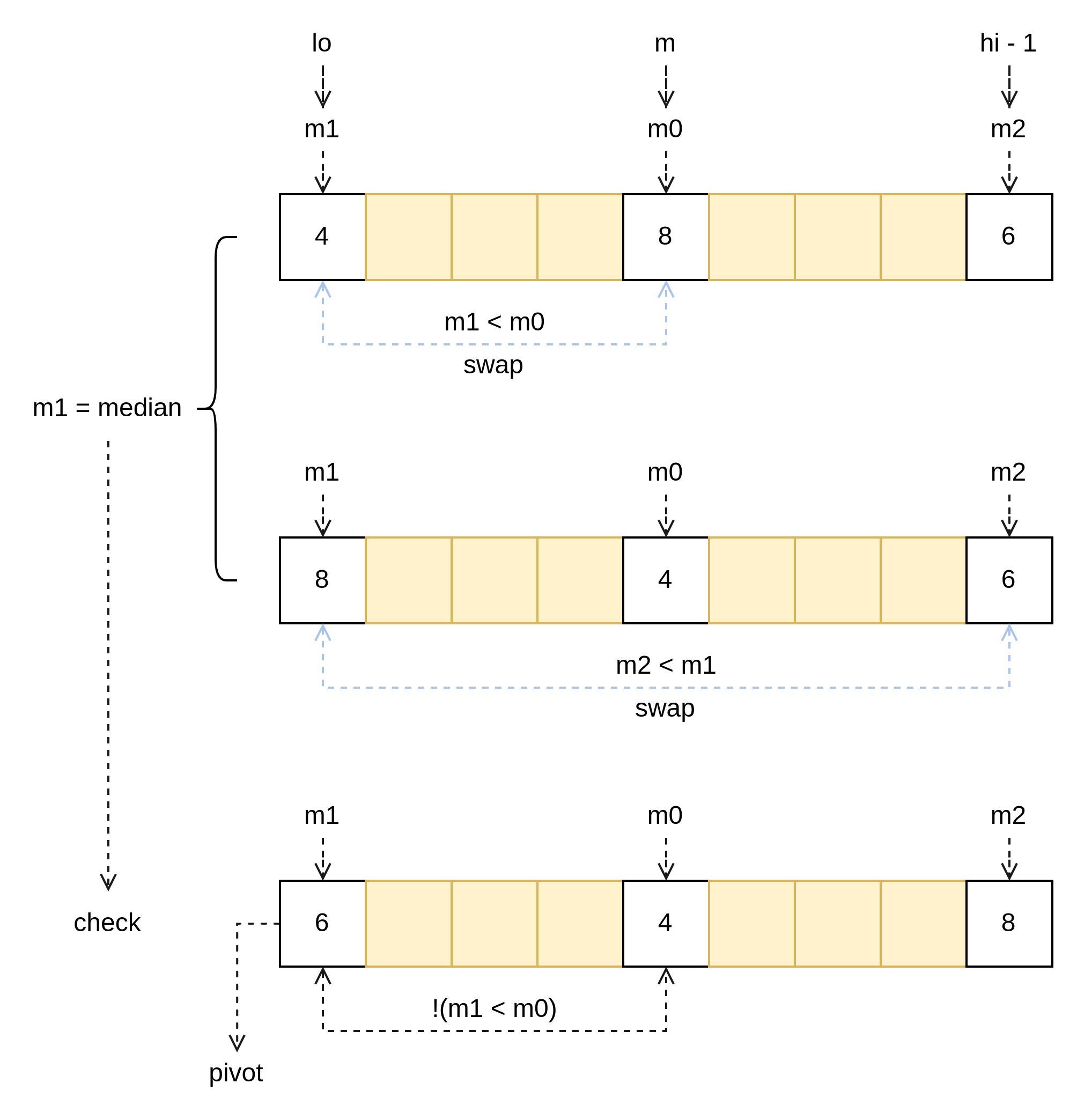
以下为 doPivot 方法中使用的 medianOfThree 方法的源码，L1 注释清楚的解释了这个方法的作用，即把 m0、m1、m2 这三个索引位置的的元素中的中位数放入索引 m1（lo）中，并且如图 2 所示，在任何情况下保持 data[m0] <= data[m1] <= data[m2] 的关系。

  1. // medianOfThree moves the median of the three values data[m0], data[m1], data[m2] into data[m1].
  2. func medianOfThree(data Interface, m1, m0, m2 int) {
  3.     // sort 3 elements
  4.     if data.Less(m1, m0) {
  5.         data.Swap(m1, m0)
  6.     }
  7.     // data[m0] <= data[m1]
  8.     if data.Less(m2, m1) {
  9.         data.Swap(m2, m1)
  10.         // data[m0] <= data[m2] && data[m1] < data[m2]
  11.         if data.Less(m1, m0) {
  12.             data.Swap(m1, m0)
  13.         }
  14.     }
  15.     // now data[m0] <= data[m1] <= data[m2]
  16. }

图片.png
我们再看 doPivot 方法本身，L2 取排序区间的中间索引，使用 uint 类型转换来防止 lo + hi 溢出，这在 Go 是一种常用的手法， L3 如果元素数量大于40 则在 L6 ～ L8 执行三次 medianOfThree，否则只执行一次 medianOfThree，这么做依然是为了保 证后续找到的 pivot 更接近中位数，我们使元素数量为 41 看一下四次 medianOfThree 的情况，由于每次执行更改的位置互不冲突，我们合成一张图来看一下。

图片.png
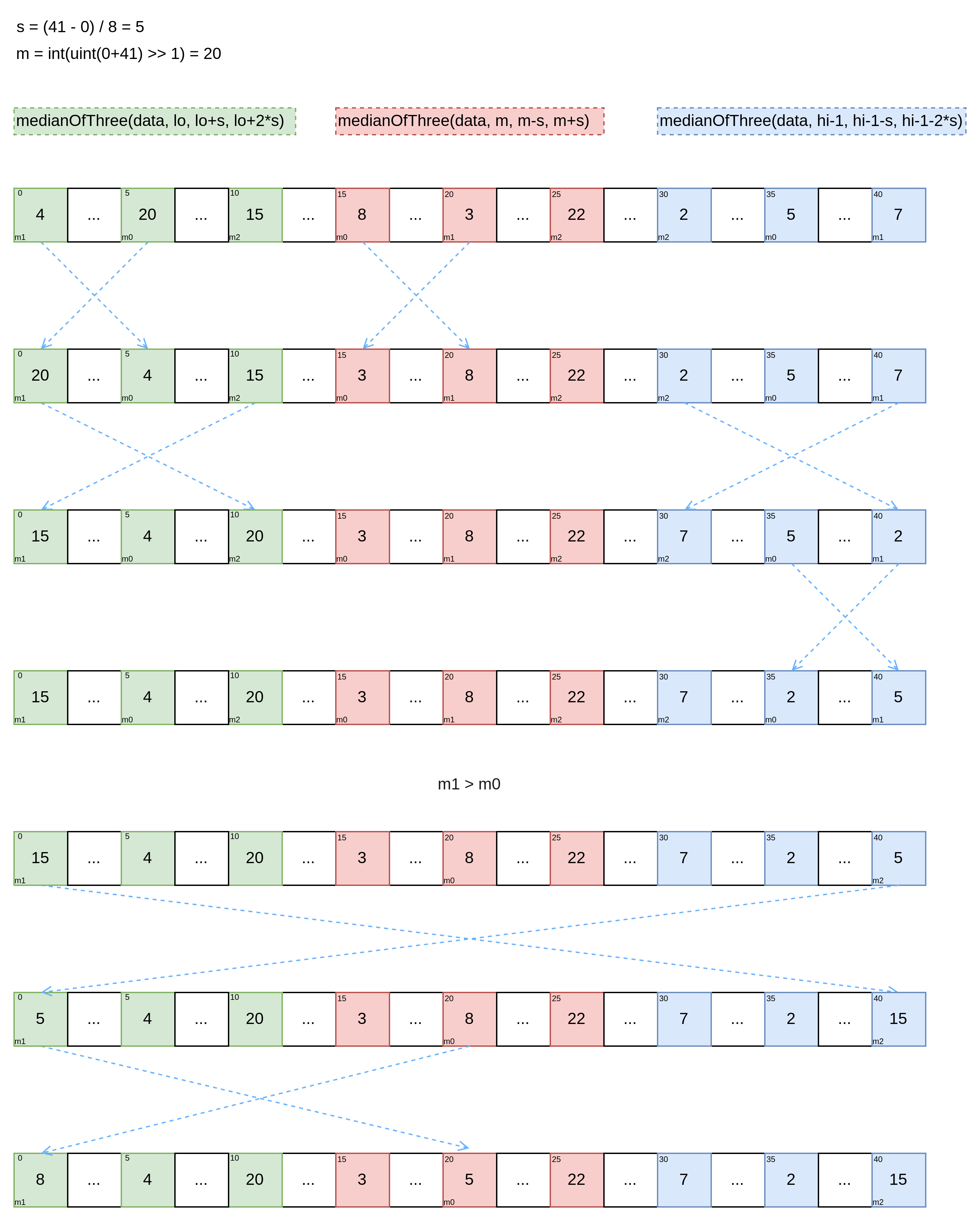
回到 doPivot 的 L19， lo 为最后一次 medianOfThree 选出的 pivot，L20 中由于 lo 为 pivot 所以 a 取 lo + 1，紧接着 L22 ～ L37 为分区逻辑，我们一行一行来看。

L22 ～ L23 因为小于 pivot 的值要放在左侧，所以 a 跳过所有小于 pivot 的元素从第一个大于等于 pivot 的元素下标开始，L24 使 b 等于 a ，在接下来的分区过程中使用。L26 ～ L27，找到第一个大于等于 pivot 的下标，L28 ～ L29 找到第一个小于等于 pivot 的值，因为在之前的 medianOfThree 中已经确保 pivot < hi - 1，所以这里从 c - 1 下标开始寻找，L30 ～ L32 中 b >= c 说明已经查找完毕，跳出循环，L34 交换之前找到的两个下标中的元素。

L40 ～ L82 为某种优化逻辑，从注释来看是某种保护措施，我们暂时忽略。L84 把 pivot 放到中间位置，然后在 L85 返回 b -1 与 c 两个下标，其中 b - 1 是我们 pivot 的位置，c 为 pivot 后一位。

  1. func doPivot(data Interface, lo, hi int) (midlo, midhi int) {
  2.     m := int(uint(lo+hi) >> 1) // Written like this to avoid integer overflow.
  3.     if hi-lo > 40 {
  4.         // Tukey's ``Ninther,'' median of three medians of three.
  5.         s := (hi - lo) / 8
  6.         medianOfThree(data, lo, lo+s, lo+2*s)
  7.         medianOfThree(data, m, m-s, m+s)
  8.         medianOfThree(data, hi-1, hi-1-s, hi-1-2*s)
  9.     }
  10.     medianOfThree(data, lo, m, hi-1)
  12.     // Invariants are:
  13.     //    data[lo] = pivot (set up by ChoosePivot)
  14.     //    data[lo < i < a] < pivot
  15.     //    data[a <= i < b] <= pivot
  16.     //    data[b <= i < c] unexamined
  17.     //    data[c <= i < hi-1] > pivot
  18.     //    data[hi-1] >= pivot
  19.     pivot := lo
  20.     a, c := lo+1, hi-1
  22.     for ; a < c && data.Less(a, pivot); a++ {
  23.     }
  24.     b := a
  25.     for {
  26.         for ; b < c && !data.Less(pivot, b); b++ { // data[b] <= pivot
  27.         }
  28.         for ; b < c && data.Less(pivot, c-1); c-- { // data[c-1] > pivot
  29.         }
  30.         if b >= c {
  31.             break
  32.         }
  33.         // data[b] > pivot; data[c-1] <= pivot
  34.         data.Swap(b, c-1)
  35.         b++
  36.         c--
  37.     }
  38.     // If hi-c<3 then there are duplicates (by property of median of nine).
  39.     // Let's be a bit more conservative, and set border to 5.
  40.     protect := hi-c < 5
  41.     if !protect && hi-c < (hi-lo)/4 {
  42.         // Lets test some points for equality to pivot
  43.         dups := 0
  44.         if !data.Less(pivot, hi-1) { // data[hi-1] = pivot
  45.             data.Swap(c, hi-1)
  46.             c++
  47.             dups++
  48.         }
  49.         if !data.Less(b-1, pivot) { // data[b-1] = pivot
  50.             b--
  51.             dups++
  52.         }
  53.         // m-lo = (hi-lo)/2 > 6
  54.         // b-lo > (hi-lo)*3/4-1 > 8
  55.         // ==> m < b ==> data[m] <= pivot
  56.         if !data.Less(m, pivot) { // data[m] = pivot
  57.             data.Swap(m, b-1)
  58.             b--
  59.             dups++
  60.         }
  61.         // if at least 2 points are equal to pivot, assume skewed distribution
  62.         protect = dups > 1
  63.     }
  64.     if protect {
  65.         // Protect against a lot of duplicates
  66.         // Add invariant:
  67.         //    data[a <= i < b] unexamined
  68.         //    data[b <= i < c] = pivot
  69.         for {
  70.             for ; a < b && !data.Less(b-1, pivot); b-- { // data[b] == pivot
  71.             }
  72.             for ; a < b && data.Less(a, pivot); a++ { // data[a] < pivot
  73.             }
  74.             if a >= b {
  75.                 break
  76.             }
  77.             // data[a] == pivot; data[b-1] < pivot
  78.             data.Swap(a, b-1)
  79.             a++
  80.             b--
  81.         }
  82.     }
  83.     // Swap pivot into middle
  84.     data.Swap(pivot, b-1)
  85.     return b - 1, c
  86. }

现在我们回过头来再看 quickSort 的 L13 ～ L19， 这时便能理解 L10 中 mlo 与 mhi 的含义是为了比较 lo 到 median 和 median + 1 到 hi - 1 两个区间的长度，然后选择更小的区间进行下一次迭代，直到 maxDepth 为 0 之后执行 heapSort 或者某次传入的区间元素数量小于等于 12 之后进行 shellSort 和 insertSort。和图 1 的 quickSort 不同，L13 ～ L19 的逻辑是 if else，也就是说只会对较小区间进行迭代另一部分则不会进行分区迭代，接下来我们看 heapSort。

  1. // ...
  3. func quickSort(data Interface, a, b, maxDepth int) {
  4.     for b-a > 12 { // Use ShellSort for slices <= 12 elements
  5.         if maxDepth == 0 {
  6.             heapSort(data, a, b)
  7.             return
  8.         }
  9.         maxDepth--
  10.         mlo, mhi := doPivot(data, a, b)
  11.         // Avoiding recursion on the larger subproblem guarantees
  12.         // a stack depth of at most lg(b-a).
  13.         if mlo-a < b-mhi {
  14.             quickSort(data, a, mlo, maxDepth)
  15.             a = mhi // i.e., quickSort(data, mhi, b)
  16.         } else {
  17.             quickSort(data, mhi, b, maxDepth)
  18.             b = mlo // i.e., quickSort(data, a, mlo)
  19.         }
  20.     }
  21.     if b-a > 1 {
  22.         // Do ShellSort pass with gap 6
  23.         // It could be written in this simplified form cause b-a <= 12
  24.         for i := a + 6; i < b; i++ {
  25.             if data.Less(i, i-6) {
  26.                 data.Swap(i, i-6)
  27.             }
  28.         }
  29.         insertionSort(data, a, b)
  30.     }
  31. }
  33. //...

Heap

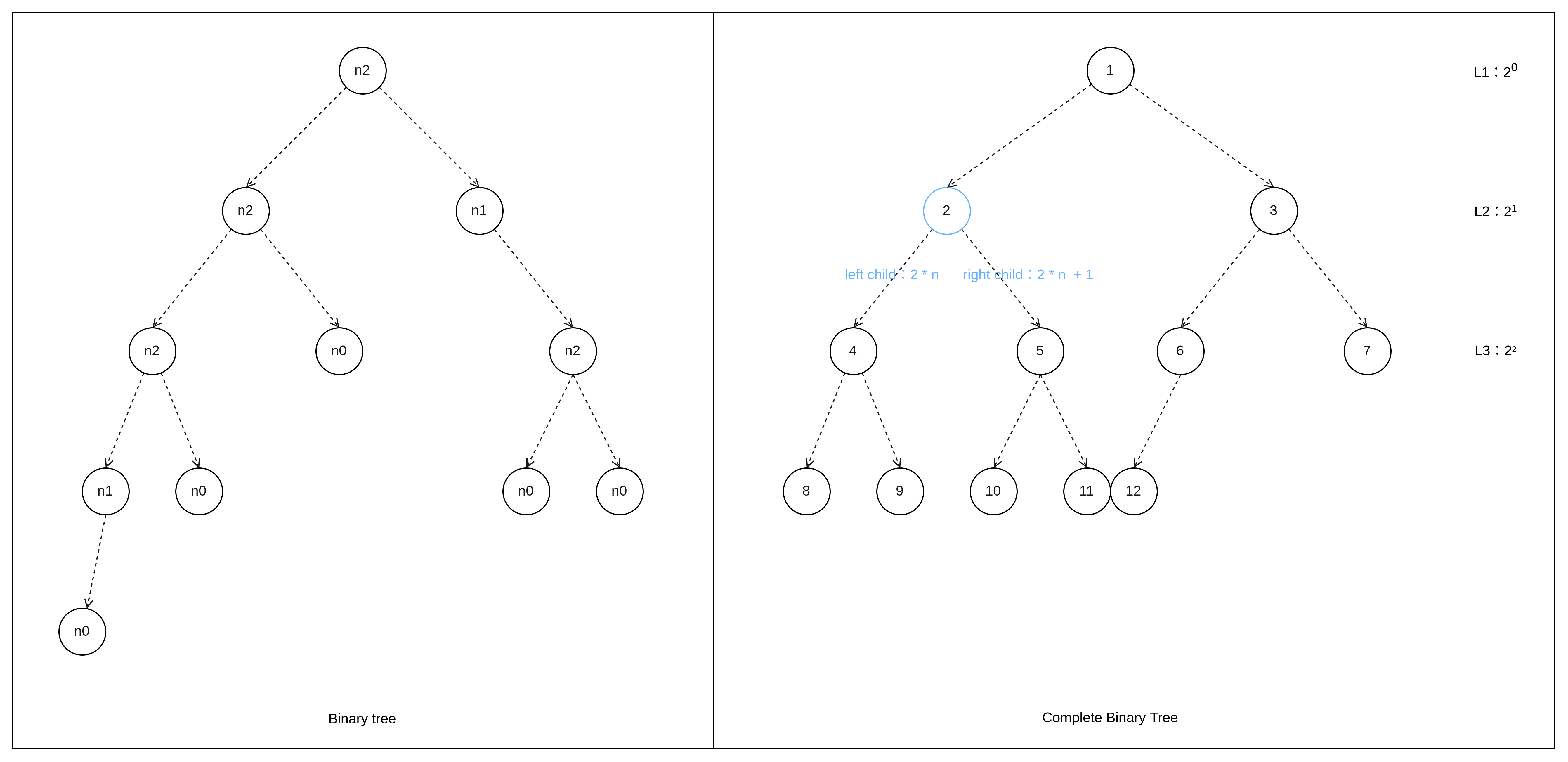
想要理解 heapSort 就必须先简单了解一下二叉树以及完全二叉树和二叉堆，我们先来看二叉树，图 4 左为 binary Tree 普通二叉树，是每个节点最多拥有两个子节点的节点树，并且节点有左右之分，不能随意颠倒顺序。

图 4 右为 complete binary tree（完全二叉树），也就是说如果一个二叉树除最后一层以外，其它层都是满的，并且最后一层要么是满的，要么节点只在右边顺序分布，那么它就是完全二叉树。 complete binary tree 根节点对应的编号为 1时，每个节点的左右子节点，分别为 n 2 和 n 2 + 1，并且父节点为 n / 2，并且每层节点数量最大为 2l - 1 个，整颗 complete binary tree 最少有 2l - 1 个节点，最大有 2l - 1 个节点。

而二叉堆则是一种满足 complete binary tree 或者近似 complete binary tree 的特殊的堆，如果它的每个节点都大于其子节点，那么叫做最大堆，反之叫做最小堆。

关于二叉树我们暂时先了解这么多，之后的其它文章会详细讲解堆和二叉树，现在我们先把注意力放在 heapSort 上。
图片.png
以下为 heapSort 方法源码，L23 中 lo 初始值等于 0，所以我们可以猜测这里的二叉树模型的根节点编号从 0 开始，而 siftDown 函数中 L6 与 L10 也证实了这一点。

来到 L27，把 (hi - 1) / 2 中的 hi - 1 替换成 n 就是 complete binary tree 中查找父节点的方法（n / 2），所以 (hi - 1) / 2 代表的是最后一个节点的父节点下标，之后使用 siftDown 创建一个最大堆，然后在 L32 ～ L33 进行排序，排序的方法是把根节点与第 i 个节点交换位置，然后用 i 之前的所有节点重新构造一个最大堆，把最大值放在根节点，重复之前的动作，最后得到升序排序的数据。接下来我们看一下 siftDown 如何实现最大堆。

  1. func heapSort(data Interface, a, b int) {
  2.     first := a
  3.     lo := 0
  4.     hi := b - a
  6.     // Build heap with greatest element at top.
  7.     for i := (hi - 1) / 2; i >= 0; i-- {
  8.         siftDown(data, i, hi, first)
  9.     }
  11.     // Pop elements, largest first, into end of data.
  12.     for i := hi - 1; i >= 0; i-- {
  13.         data.Swap(first, first+i)
  14.         siftDown(data, lo, i, first)
  15.     }
  16. }

SiftDown 方法在比较节点大小之前会先判断 child 是否 大于 hi 来检测是否越界，之后如图 5 所示，在 L10 比较 child 与 child + 1，让 chile 等于较大的一方，并且在 L13 判断 root 节点是否大于较大的子节点，如果 root 节点大，则认为已经满足最大堆，直接 return，否则交换 root 节点与 child 节点的值。因为产生了交换操作，所以交换之后的 child 及后 child 节点可能不满足最大堆，所以让 root 等于 child 然后再次对剩余节点进行堆的构建。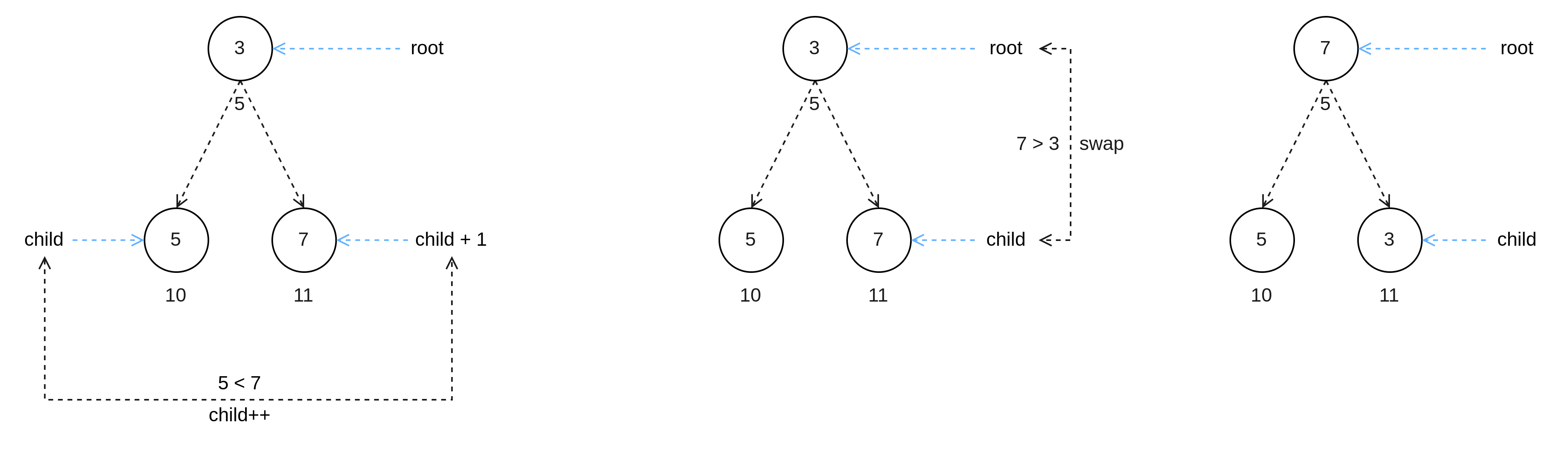
图片.png

  1. // siftDown implements the heap property on data[lo:hi].
  2. // first is an offset into the array where the root of the heap lies.
  3. func siftDown(data Interface, lo, hi, first int) {
  4.     root := lo
  5.     for {
  6.         child := 2*root + 1
  7.         if child >= hi {
  8.             break
  9.         }
  10.         if child+1 < hi && data.Less(first+child, first+child+1) {
  11.             child++
  12.         }
  13.         if !data.Less(first+root, first+child) {
  14.             return
  15.         }
  16.         data.Swap(first+root, first+child)
  17.         root = child
  18.     }
  19. }

以上就是 sort 包中的 “quickSort”方法的逻辑，不懂的朋友建议多画图去理解，许多复杂的结构其实只要把图画出来就能一目了然，同时也能加深印象，本周的内容就到这里，下周我们继续来看 sort 包中的稳定排序部分。