Grow && Copy
在 Go 语言中,slice 的 cap 是不能直接增加的,例如,如果我们想把一个 slice 的 cap 改为之前的 2 倍,需要创建一个新 slice ,然后使新 slice 的 cap 为原 slice 的 2 倍,之后再把原 slice 中的内容 copy 到新 slice 然后再让原 slice 等于新 slice,听起来有些绕,来看一下图解。
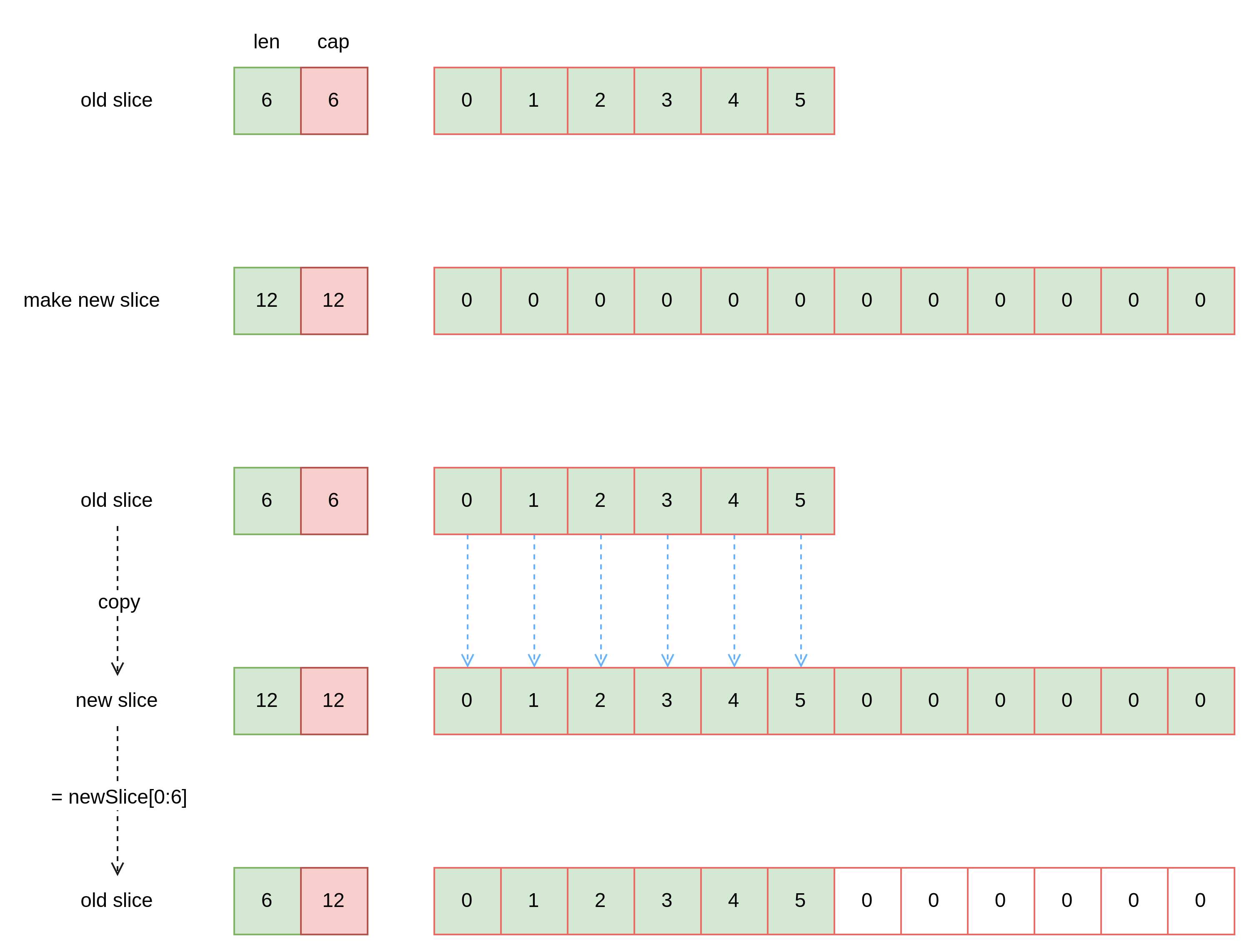
其中 copy 方法会自动判断并选择较小的长度进行复制,比如长度 6 的 slice 如果要 copy 到长度为 3 的 slice 中,那么只会 copy 前三个元素,这部分逻辑在源码 L2 ~ L9 可以清晰的看到,长度默认等于原 slice 长度,如果目标长度小于原 slice 长度,则长度为目标长度。
func slicecopy(toPtr unsafe.Pointer, toLen int, fromPtr unsafe.Pointer, fromLen int, width uintptr) int {if fromLen == 0 || toLen == 0 {return 0}n := fromLenif toLen < n {n = toLen}if width == 0 {return n}size := uintptr(n) * widthif raceenabled {callerpc := getcallerpc()pc := abi.FuncPCABIInternal(slicecopy)racereadrangepc(fromPtr, size, callerpc, pc)racewriterangepc(toPtr, size, callerpc, pc)}if msanenabled {msanread(fromPtr, size)msanwrite(toPtr, size)}if asanenabled {asanread(fromPtr, size)asanwrite(toPtr, size)}if size == 1 { // common case worth about 2x to do here// TODO: is this still worth it with new memmove impl?*(*byte)(toPtr) = *(*byte)(fromPtr) // known to be a byte pointer} else {memmove(toPtr, fromPtr, size)}return n}
在 copy 时,如果双方共用一个底层数组,则需要注意一下由指针带来的底层数组变动,比如在下例中,原 slice 在进行 copy 之后被意外的修改。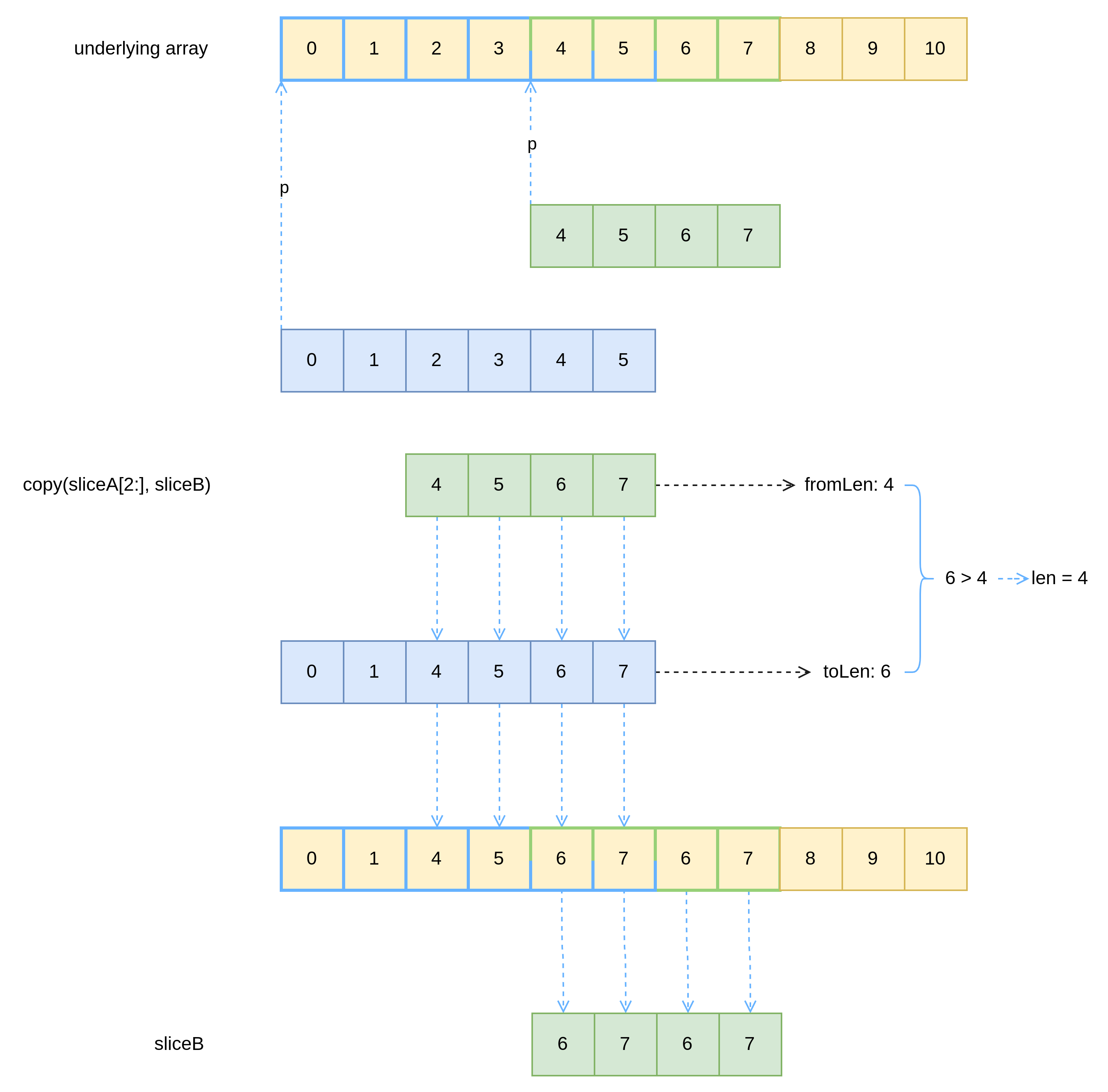
Append
Append 方法的作用是向一个 slice 中追加内容,如果目标 slice 剩余 cap 不足以存放追加内容,则会自动扩容,需要注意的是,在扩容时会声明另一个底层数组,并且使 slice 的 ptr 重新指向新的底层数组,反之会继续延用之前的底层数组,图 3 和 图 4 分别对应以上两种情况。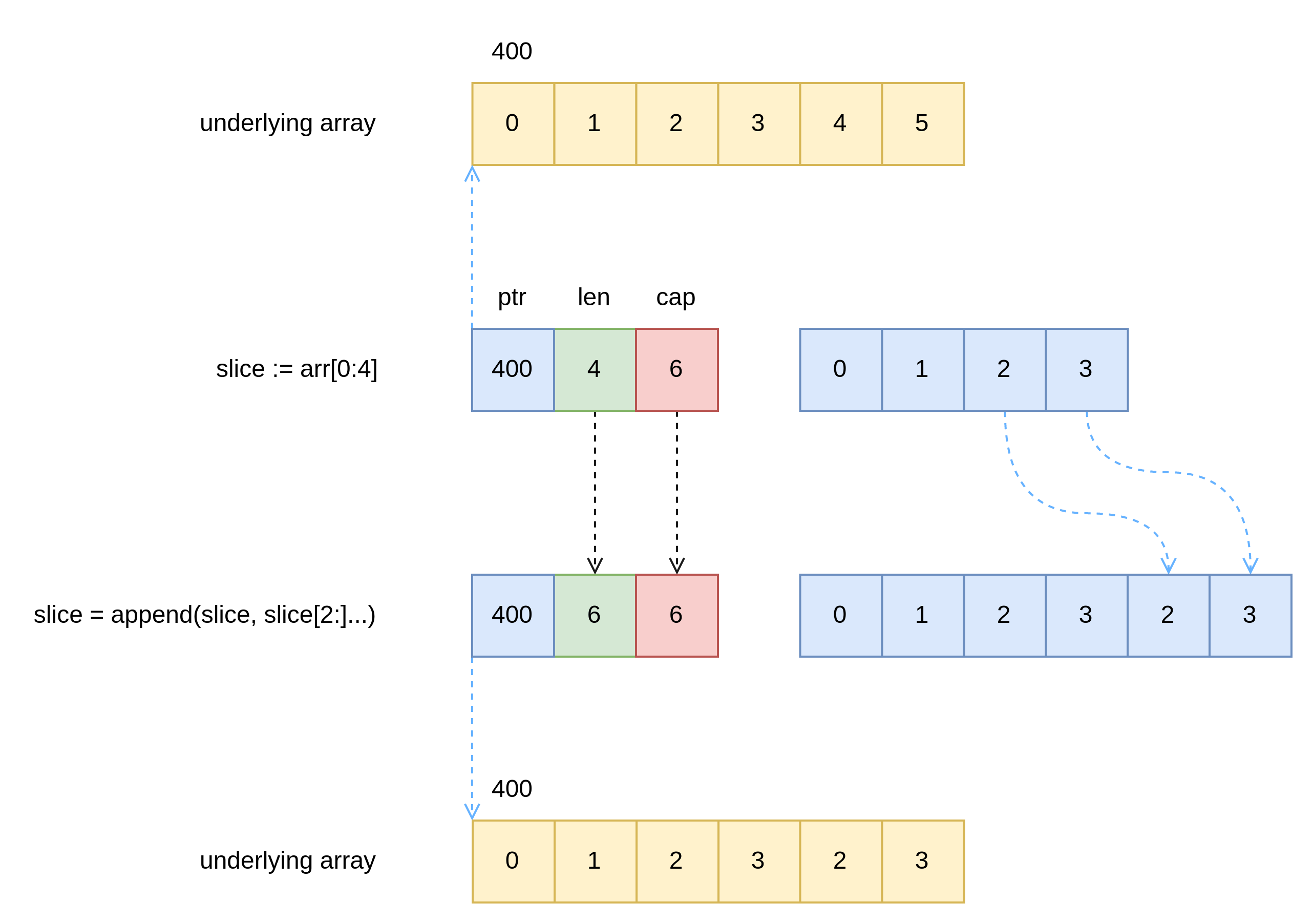
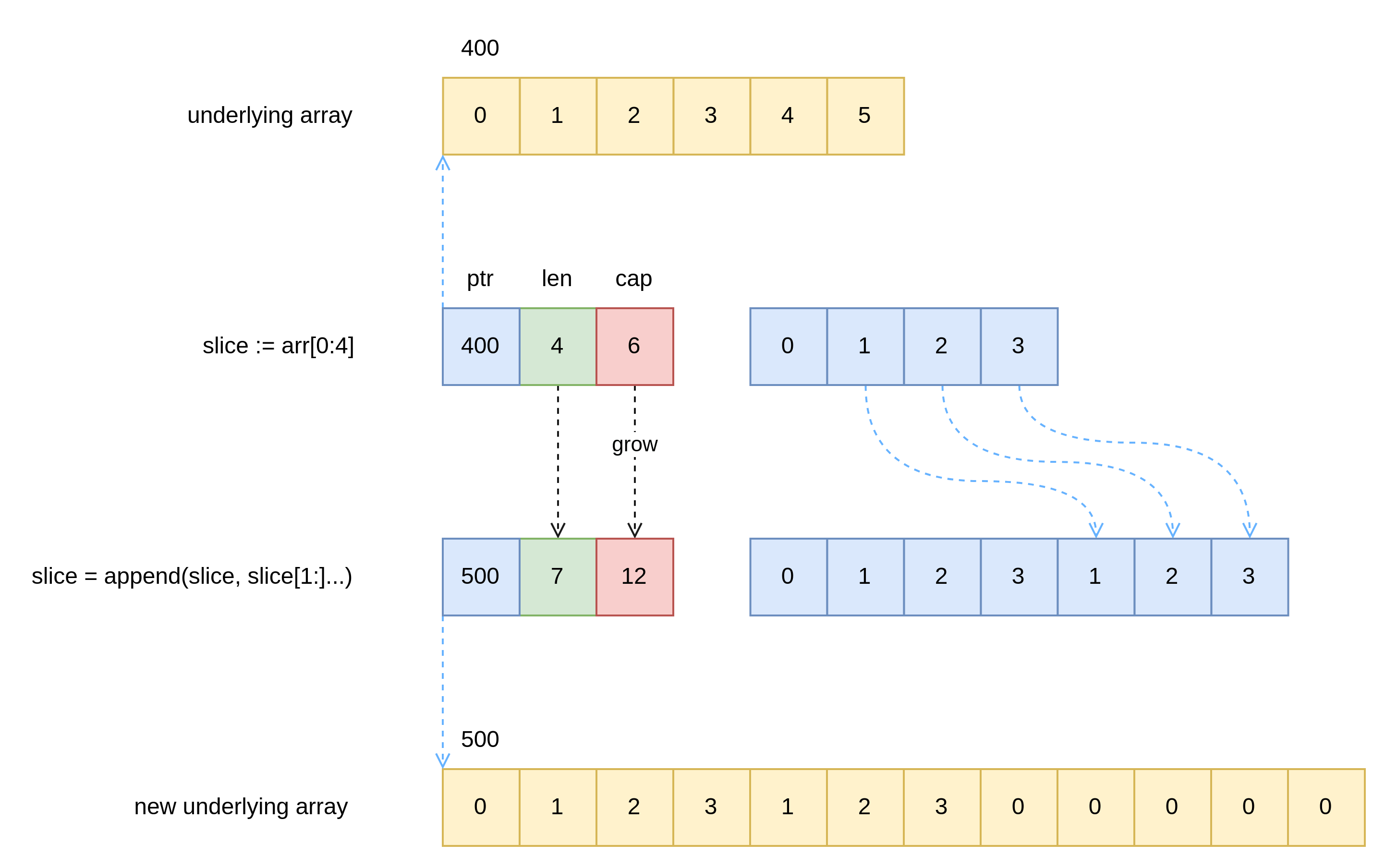
Append-grow
Slice 在 append 时会自动扩容,下面我们来看看扩容的规则。
func growslice(et *_type, old slice, cap int) slice {if raceenabled {callerpc := getcallerpc()racereadrangepc(old.array, uintptr(old.len*int(et.size)), callerpc, abi.FuncPCABIInternal(growslice))}if msanenabled {msanread(old.array, uintptr(old.len*int(et.size)))}if asanenabled {asanread(old.array, uintptr(old.len*int(et.size)))}if cap < old.cap {panic(errorString("growslice: cap out of range"))}if et.size == 0 {// append should not create a slice with nil pointer but non-zero len.// We assume that append doesn't need to preserve old.array in this case.return slice{unsafe.Pointer(&zerobase), old.len, cap}}newcap := old.capdoublecap := newcap + newcapif cap > doublecap {newcap = cap} else {const threshold = 256if old.cap < threshold {newcap = doublecap} else {// Check 0 < newcap to detect overflow// and prevent an infinite loop.for 0 < newcap && newcap < cap {// Transition from growing 2x for small slices// to growing 1.25x for large slices. This formula// gives a smooth-ish transition between the two.newcap += (newcap + 3*threshold) / 4}// Set newcap to the requested cap when// the newcap calculation overflowed.if newcap <= 0 {newcap = cap}}}var overflow boolvar lenmem, newlenmem, capmem uintptr// Specialize for common values of et.size.// For 1 we don't need any division/multiplication.// For goarch.PtrSize, compiler will optimize division/multiplication into a shift by a constant.// For powers of 2, use a variable shift.switch {case et.size == 1:lenmem = uintptr(old.len)newlenmem = uintptr(cap)capmem = roundupsize(uintptr(newcap))overflow = uintptr(newcap) > maxAllocnewcap = int(capmem)case et.size == goarch.PtrSize:lenmem = uintptr(old.len) * goarch.PtrSizenewlenmem = uintptr(cap) * goarch.PtrSizecapmem = roundupsize(uintptr(newcap) * goarch.PtrSize)overflow = uintptr(newcap) > maxAlloc/goarch.PtrSizenewcap = int(capmem / goarch.PtrSize)case isPowerOfTwo(et.size):var shift uintptrif goarch.PtrSize == 8 {// Mask shift for better code generation.shift = uintptr(sys.Ctz64(uint64(et.size))) & 63} else {shift = uintptr(sys.Ctz32(uint32(et.size))) & 31}lenmem = uintptr(old.len) << shiftnewlenmem = uintptr(cap) << shiftcapmem = roundupsize(uintptr(newcap) << shift)overflow = uintptr(newcap) > (maxAlloc >> shift)newcap = int(capmem >> shift)default:lenmem = uintptr(old.len) * et.sizenewlenmem = uintptr(cap) * et.sizecapmem, overflow = math.MulUintptr(et.size, uintptr(newcap))capmem = roundupsize(capmem)newcap = int(capmem / et.size)}// The check of overflow in addition to capmem > maxAlloc is needed// to prevent an overflow which can be used to trigger a segfault// on 32bit architectures with this example program://// type T [1<<27 + 1]int64//// var d T// var s []T//// func main() {// s = append(s, d, d, d, d)// print(len(s), "\n")// }if overflow || capmem > maxAlloc {panic(errorString("growslice: cap out of range"))}var p unsafe.Pointerif et.ptrdata == 0 {p = mallocgc(capmem, nil, false)// The append() that calls growslice is going to overwrite from old.len to cap (which will be the new length).// Only clear the part that will not be overwritten.memclrNoHeapPointers(add(p, newlenmem), capmem-newlenmem)} else {// Note: can't use rawmem (which avoids zeroing of memory), because then GC can scan uninitialized memory.p = mallocgc(capmem, et, true)if lenmem > 0 && writeBarrier.enabled {// Only shade the pointers in old.array since we know the destination slice p// only contains nil pointers because it has been cleared during alloc.bulkBarrierPreWriteSrcOnly(uintptr(p), uintptr(old.array), lenmem-et.size+et.ptrdata)}}memmove(p, old.array, lenmem)return slice{p, old.len, newcap}}
观察源码,slice 主要的扩容逻辑在 L23 ~ L46 ,主要分为以下三种情况。
- 原 slice 容量小于 256,并且最小需求容量小于二倍原 slice 容量。
- 原 slice 容量大于 256,并且最小需求容量小于二倍原 slice 容量。
- 最小需求容量大于二倍原 slice 容量。
在第一种情况中,容量会直接乘 2,第二种情况中容量的增长量会随着原容量越来越大而过渡到 1.25 倍,注意是过渡,而不是立刻变为 1.25 倍,接下来我们来看一下测试。
func main() {testing := make([]int, 0)appendRange := math.MaxInt64lastCap := 0for i := 0; i <= appendRange; i++ {testing = append(testing, i)nowCap := cap(testing)if (nowCap != lastCap) {fmt.Printf("append: %9d, addr: %p, len: %9d, cap: %9d -- %9f;\n",i, testing, len(testing), nowCap,float32(nowCap) / float32(lastCap))}lastCap = nowCap}}//append: 0, addr: 0xc0000a6000, len: 1, cap: 1 -- +Inf;//append: 1, addr: 0xc0000a6020, len: 2, cap: 2 -- 2.000000;//append: 2, addr: 0xc0000b0000, len: 3, cap: 4 -- 2.000000;//append: 4, addr: 0xc0000a0040, len: 5, cap: 8 -- 2.000000;//append: 8, addr: 0xc0000b2000, len: 9, cap: 16 -- 2.000000;//append: 16, addr: 0xc0000b4000, len: 17, cap: 32 -- 2.000000;//append: 32, addr: 0xc0000b6000, len: 33, cap: 64 -- 2.000000;//append: 64, addr: 0xc0000b8000, len: 65, cap: 128 -- 2.000000;//append: 128, addr: 0xc0000ba000, len: 129, cap: 256 -- 2.000000;//append: 256, addr: 0xc0000bc000, len: 257, cap: 512 -- 2.000000;//append: 512, addr: 0xc0000be000, len: 513, cap: 848 -- 1.656250;//append: 848, addr: 0xc0000c8000, len: 849, cap: 1280 -- 1.509434;//append: 1280, addr: 0xc0000d2000, len: 1281, cap: 1792 -- 1.400000;//append: 1792, addr: 0xc0000e0000, len: 1793, cap: 2560 -- 1.428571;//append: 2560, addr: 0xc0000ea000, len: 2561, cap: 3408 -- 1.331250;//append: 3408, addr: 0xc000100000, len: 3409, cap: 5120 -- 1.502347;//append: 5120, addr: 0xc00010a000, len: 5121, cap: 7168 -- 1.400000;//append: 7168, addr: 0xc000118000, len: 7169, cap: 9216 -- 1.285714;//append: 9216, addr: 0xc00012a000, len: 9217, cap: 12288 -- 1.333333;//append: 12288, addr: 0xc000142000, len: 12289, cap: 16384 -- 1.333333;//append: 16384, addr: 0xc000162000, len: 16385, cap: 21504 -- 1.312500;//append: 21504, addr: 0xc00018c000, len: 21505, cap: 27648 -- 1.285714;//append: 27648, addr: 0xc0001c2000, len: 27649, cap: 34816 -- 1.259259;//append: 34816, addr: 0xc000206000, len: 34817, cap: 44032 -- 1.264706;//append: 44032, addr: 0xc00025c000, len: 44033, cap: 55296 -- 1.255814;//append: 55296, addr: 0xc0002c8000, len: 55297, cap: 69632 -- 1.259259;//append: 69632, addr: 0xc000350000, len: 69633, cap: 88064 -- 1.264706;//append: 88064, addr: 0xc0003fc000, len: 88065, cap: 110592 -- 1.255814;//append: 110592, addr: 0xc000100000, len: 110593, cap: 139264 -- 1.259259;//append: 139264, addr: 0xc000210000, len: 139265, cap: 175104 -- 1.257353;//append: 175104, addr: 0xc0004d4000, len: 175105, cap: 219136 -- 1.251462;//append: 219136, addr: 0xc000100000, len: 219137, cap: 274432 -- 1.252337;//append: 274432, addr: 0xc000680000, len: 274433, cap: 344064 -- 1.253731;//append: 344064, addr: 0xc000100000, len: 344065, cap: 431104 -- 1.252976;//append: 431104, addr: 0xc00044a000, len: 431105, cap: 539648 -- 1.251781;//append: 539648, addr: 0xc000868000, len: 539649, cap: 674816 -- 1.250474;//append: 674816, addr: 0xc0000b2000, len: 674817, cap: 843776 -- 1.250379;//append: 843776, addr: 0xc000722000, len: 843777, cap: 1055744 -- 1.251214;//append: 1055744, addr: 0xc000f30000, len: 1055745, cap: 1319936 -- 1.250242;//append: 1319936, addr: 0xc0000b2000, len: 1319937, cap: 1650688 -- 1.250582;//append: 1650688, addr: 0xc000d4a000, len: 1650689, cap: 2064384 -- 1.250620;//append: 2064384, addr: 0xc001d0a000, len: 2064385, cap: 2581504 -- 1.250496;//append: 2581504, addr: 0xc0000b2000, len: 2581505, cap: 3227648 -- 1.250298;//append: 3227648, addr: 0xc001952000, len: 3227649, cap: 4035584 -- 1.250317;//append: 4035584, addr: 0xc00381c000, len: 4035585, cap: 5045248 -- 1.250190;//append: 5045248, addr: 0xc0000b2000, len: 5045249, cap: 6306816 -- 1.250051;//append: 6306816, addr: 0xc0030d0000, len: 6306817, cap: 7883776 -- 1.250041;//append: 7883776, addr: 0xc006cf6000, len: 7883777, cap: 9854976 -- 1.250032;//append: 9854976, addr: 0xc0000b2000, len: 9854977, cap: 12319744 -- 1.250104;
以看到 L32 ~ L48 的输出中,cap 的增长在 1.65 ~ 1.26 倍之间,之后才平缓的达到 1.25 倍。打印输出的方式看起来可能不太直观,如果我们使用图表的形式看观察可以很清楚的看到一条由 2 到 1.25“过渡”的曲线。
最后就是第三种情况,这种情况下,只看源码的 L25 L26 行容量是等于最小需求容量的,但是在测试中发现,并不是简单的等于关系,Go 在之后的处理中会对计算出的新容量进行内存对齐,对此我们暂时不做深究。
func main() {for i := 0; i < 200; i++ {testing := make([]int, 5)testing = append(testing, make([]int, i)...)fmt.Printf("number: %d, len: %d, cap: %d; \n", i, len(testing), cap(testing))}}// number: 0, len: 5, cap: 5;// number: 1, len: 6, cap: 10;// number: 2, len: 7, cap: 10;// number: 3, len: 8, cap: 10;// number: 4, len: 9, cap: 10;// number: 5, len: 10, cap: 10;// number: 6, len: 11, cap: 12;// number: 7, len: 12, cap: 12;// number: 8, len: 13, cap: 14;// number: 9, len: 14, cap: 14;// number: 10, len: 15, cap: 16;// number: 11, len: 16, cap: 16;// number: 12, len: 17, cap: 18;// number: 13, len: 18, cap: 18;// number: 14, len: 19, cap: 20;// number: 15, len: 20, cap: 20;// number: 16, len: 21, cap: 22;// number: 17, len: 22, cap: 22;// number: 18, len: 23, cap: 24;// number: 19, len: 24, cap: 24;// number: 20, len: 25, cap: 26;// number: 21, len: 26, cap: 26;// number: 22, len: 27, cap: 28;// number: 23, len: 28, cap: 28;// number: 24, len: 29, cap: 30;// number: 25, len: 30, cap: 30;// number: 26, len: 31, cap: 32;// number: 27, len: 32, cap: 32;// number: 28, len: 33, cap: 36;// number: 29, len: 34, cap: 36;// number: 30, len: 35, cap: 36;// number: 31, len: 36, cap: 36;// number: 32, len: 37, cap: 40;// number: 33, len: 38, cap: 40;// number: 34, len: 39, cap: 40;// number: 35, len: 40, cap: 40;// number: 36, len: 41, cap: 44;// number: 37, len: 42, cap: 44;// number: 38, len: 43, cap: 44;// number: 39, len: 44, cap: 44;

