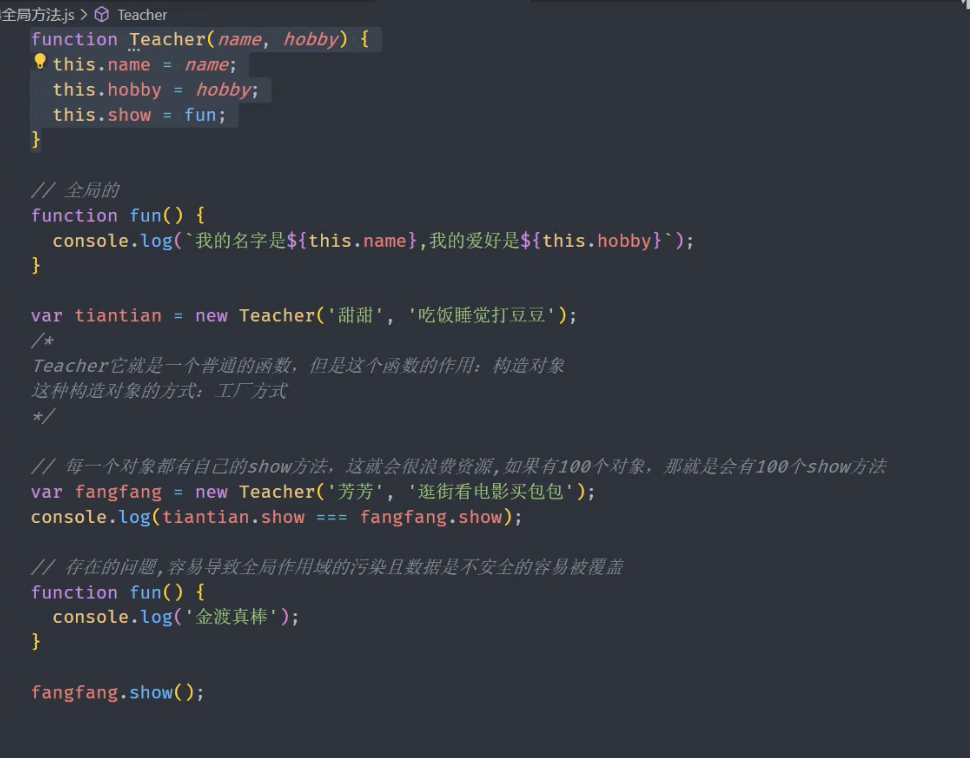
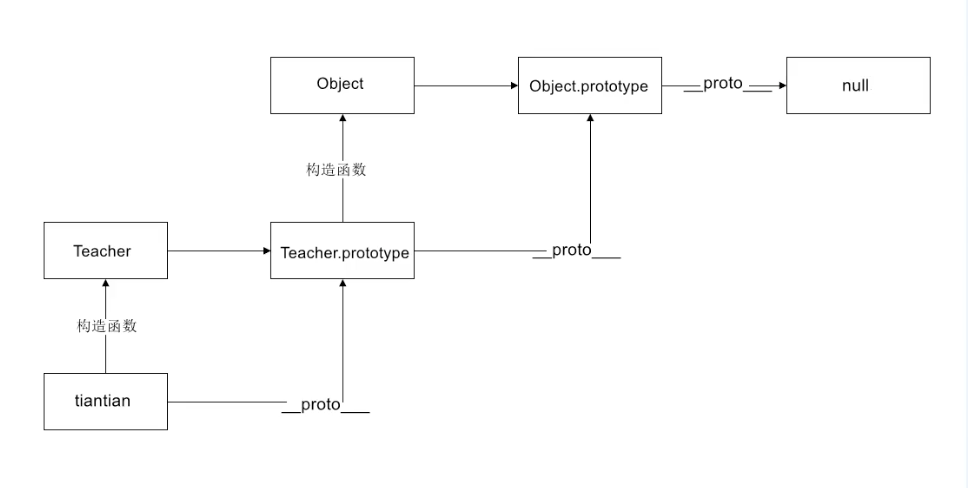
数据结构
- 数据: 描述客观事物的符号
- 能被输入到计算机中
- 能被计算机处理
- 数据对象:性质相同的数据元素的集合
- 数据元素: 数据的基本单位
- 数据项:组成数据元素原素的独立含义的不可分割的最小单位

- 线性结构:除了第一个和最后一个元素之外,其他元素都是首位相接的,比如:数组,堆栈,队列;
- .必存在第一个元素
- 必存在最后一个元素
- 除最后一个元素外,其他元素均有一个后续的元素
- 除第一个元素外,其他元素均有一个唯一的前置
- 树形结构 DOM树
- 图形结构
- 物理结构:数据元素存储到计算机的物理内存中
数据结构应该正确的反映数据元素之间的逻辑关系
- 顺序存储 开辟连续的内存空间
- 链式存储 指针,存储内存空间的地址
js数组 堆栈
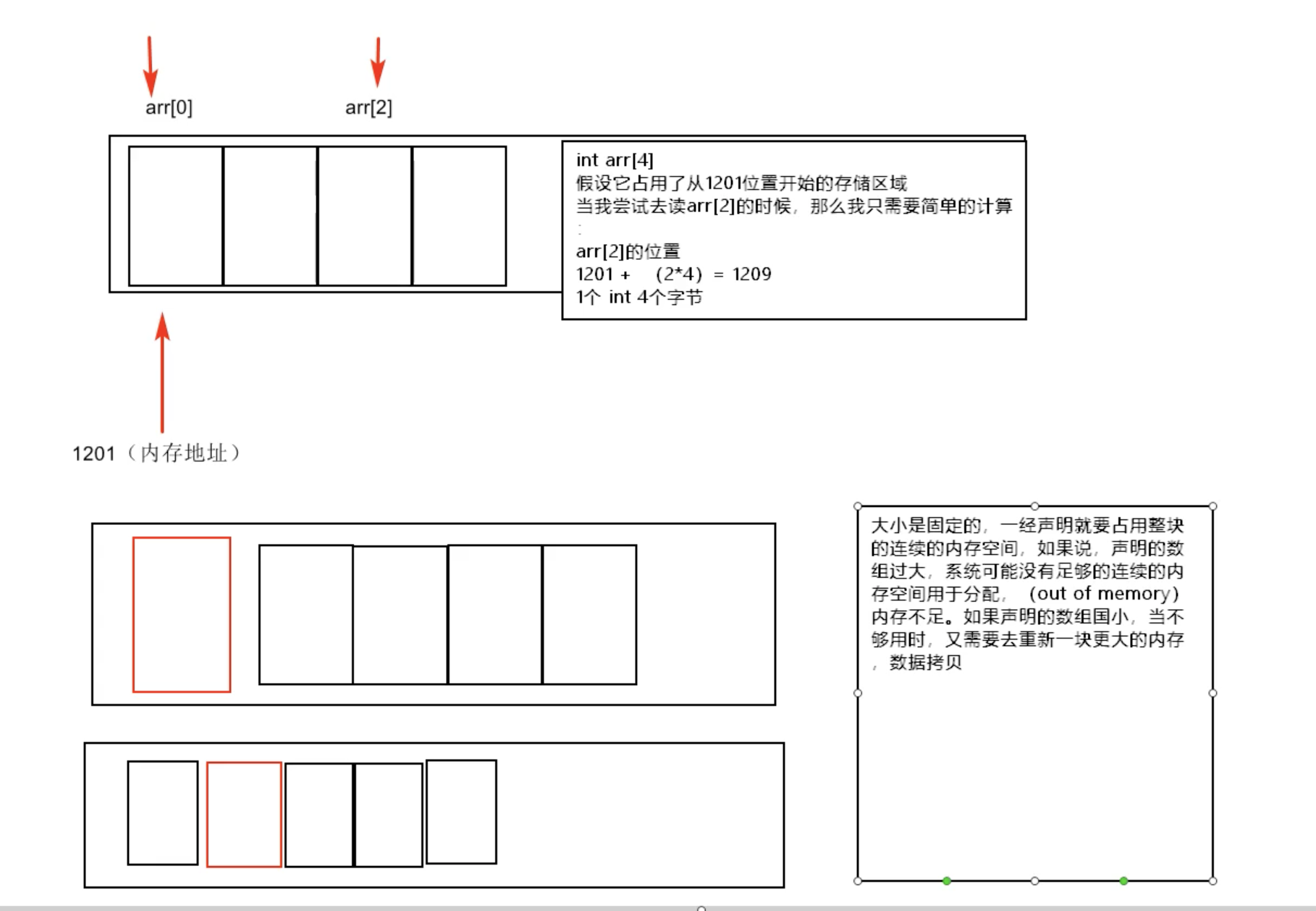
- 递归:同时保存成百上千个调用帧
- 尾调用 函数结尾调用另一个函数
- 尾递归 只存在一个调用帧
```javascript
// 尾递归优化
function fib(n,ac1=1,ac2=1){
if(n<=1){
} return fib(n-1,ac2,ac1+ac2) }return ac2;
function factor(n,total=1){ if(n===1){ return total; } return factor(n-1,total*n) }
```
链表
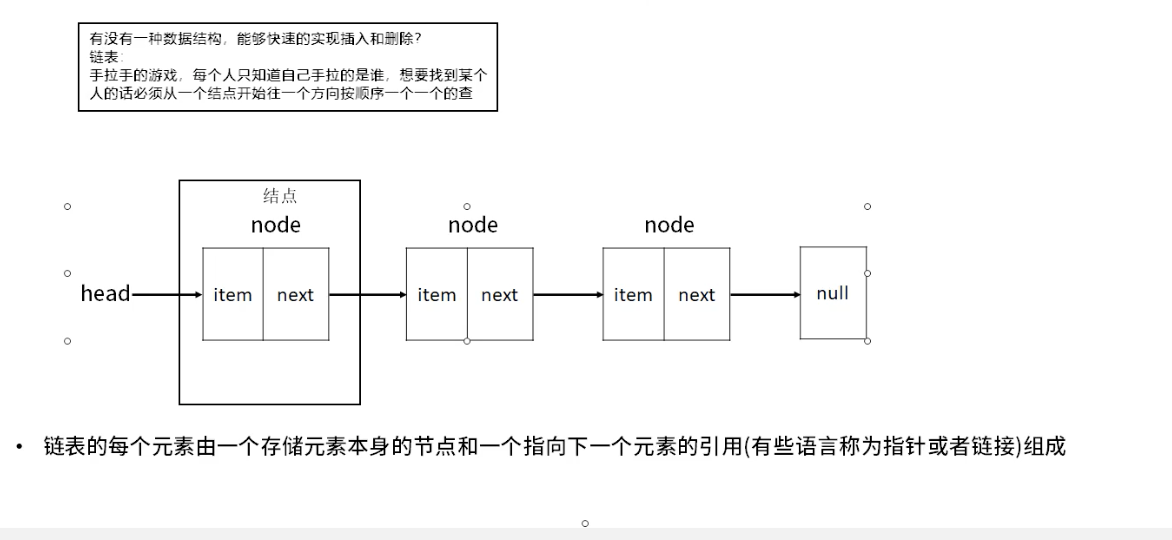
- 链表中的元素在内存中不必是连续的空间
- 每一个元素由存储元素本身和指向下一个节点的指针(引用)组成
- 插入删除性能好,支持动态扩缩容,因为链表的每个元素节点都需要保存其他节点的指针,因此消耗的内存翻倍
- 查询性能没有数组好

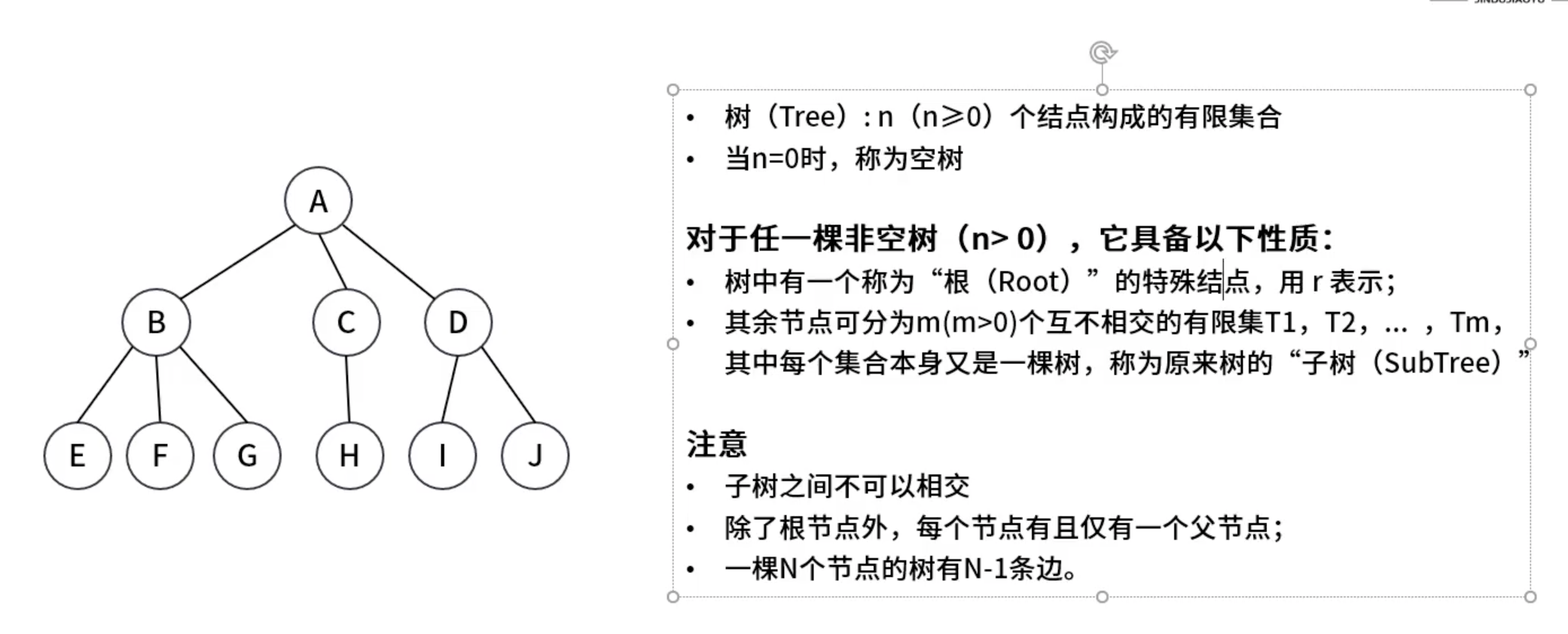
树
有N个结点的有限集,n》=0 0 为空树
1.仅根结点没有前驱结点,其他结点有一个
2.递归特性,子树又是一棵树
3.多对一,或者说一对多,每个结点都可以有多个子结点
- 术语
- 结点的度:拥有子树的个数
- 树的度:树中结点数的最大值
- 叶子:终端结点,度为0
- 分支结点:度不为0 又称内部结点
- 子结点:结点子树的根,结点的直接后驱
- 父结点:结点的直接前趋
- 兄弟结点
- 祖先结点
- 子孙结点
- 路径
- 结点的层
- 树的深度 :树中结点层数的最大值
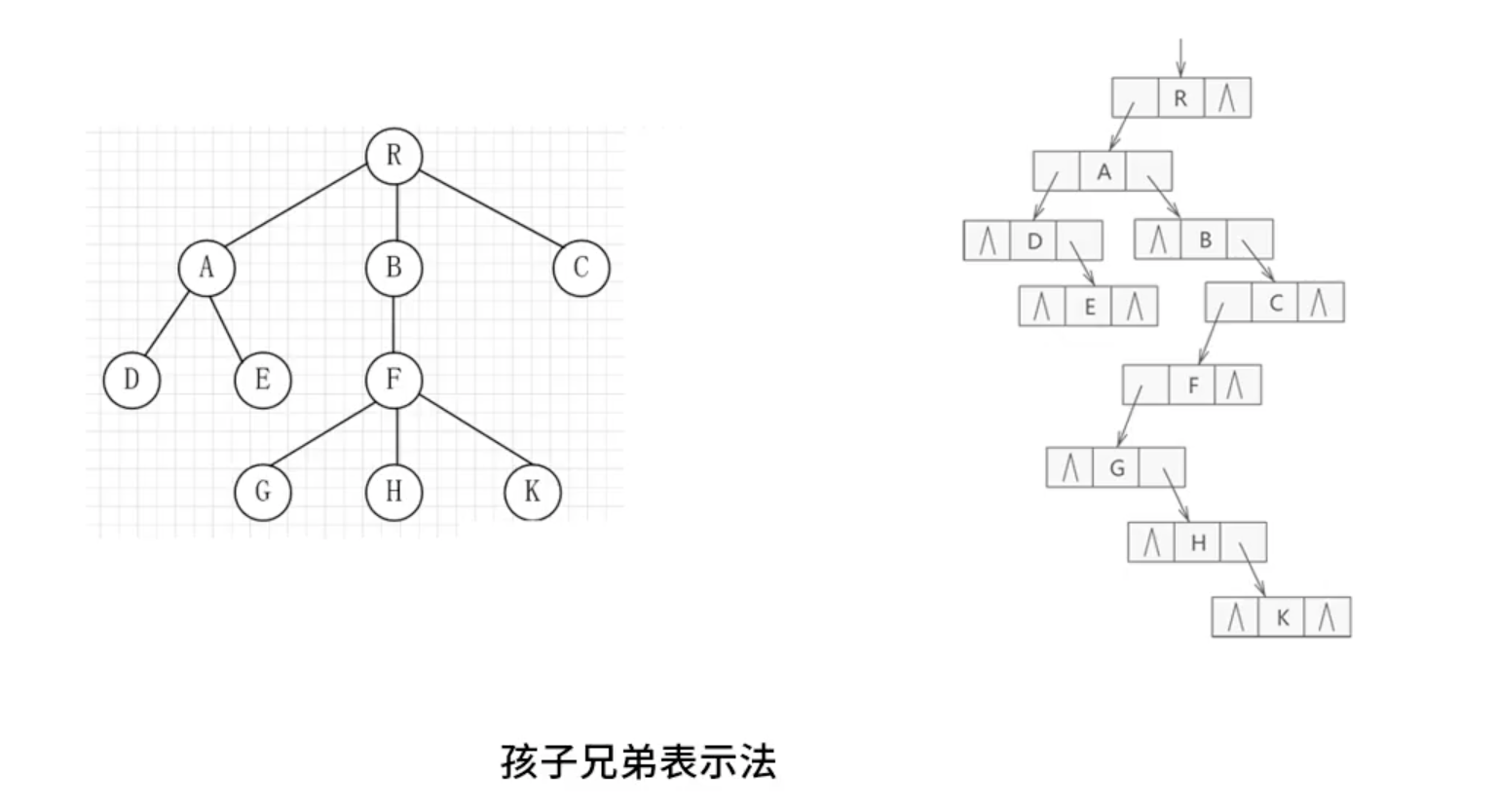
- 存储方式
- 双亲表示法:顺寻存储结点的同时,增加一个存储其存储父结点的下标的变量
- 孩子表示法:父结点用链表来存储所有他的子结点的位置信息
- 孩子兄弟表示法:孩子结点指针域+结点本身+兄弟结点指针域 转成二叉树
二叉树
- 树中的结点最多只有两个子结点
- 左子树和右子树不能颠倒
- 可以为空,如果一棵树下面只有一个子树,也要区分左右
- 满二叉树 所有分支结点都有2个子树,并且都在同一层上