Elasticsearch 中 FST 的实现原理
在3月初的时候,接到一个重构 ES 部分数据的需求,于是我开始学习了解这个 **分布式全文搜索引擎**,其中对 Lucene 中 term index 使用的数据结构 FST 比较感兴趣,在学习原理后,使用 Python 实现了一个简易版的 FST本文从第4节的内容主要翻译自 [Index 1,600,000,000 Keys with Automata and Rust](https://blog.burntsushi.net/transducers/) ,并做了一些内容上的调整,原文写得非常非常好,看完本文强烈推荐也看一下原文。文章有一些标题党的行为,其实 FST 是 Lucene 中的概念。但是直接说 Lucene 中的 FST ,可能很多人会没有兴趣。
第一节 简单介绍 Elasticsearch
Elasticsearch 是一个开源的搜索引擎,建立在一个全文搜索引擎库 Apache Lucene™ 基础之上。 Lucene 可以说是当下最先进、高性能、全功能的搜索引擎库—无论是开源还是私有。
但是 Lucene 仅仅只是一个 java 库,且 Lucene 非常 复杂。
Elasticsearch 内部使用 Lucene 做索引与搜索,通过隐藏 Lucene 的复杂性,取而代之的提供一套简单一致的 RESTful API。
然而,Elasticsearch 不仅仅是 Lucene,并且也不仅仅只是一个全文搜索引擎。 下面是它更准确的描述:
- 一个分布式 的实时文档存储,每个字段 可以被索引与搜索
- 一个分布式 实时分析搜索引擎
- 能胜任上百个服务节点的扩展,并支持 PB 级别的结构化或者非结构化数据
Elasticsearch 将所有的功能打包成一个单独的服务,这样你可以通过程序与它提供的简单的 RESTful API 进行通信, 可以使用自己喜欢的编程语言充当 web 客户端。
下面介绍一些 ES 的基本概念,文档,索引,分片,字段
// 插入一个文档,索引名为 test, 类型为 _doc, 唯一ID为1// 以 Mysql 的视角而言: 索引是一张表,文档是一条数据,ID 则为主键POST test/_doc/1 // [method] index/type/_id{"book_id": "1","title": "挪威的森林","author": "村上春树","price": 33.5,"public": "1998-03-11"}// 新数据插入以后,es 会自动添加一些元数据,以 _ 开头// 获取ID为 1 的数据GET test/_doc/1{"_index" : "test", // 文档所属的索引名"_type" : "_doc", // 文档所属的类型名"_id" : "1", // 文档的唯一ID"_version" : 1, // 文档的版本信息"_source" : { // 文档的原始 json 内容"book_id" : "1","title" : "挪威的森林","arthor" : "村上春树","price" : 33.5,"public" : "1998-03-11"}}// mapping 类似 mysql 中的列,第一次插入数据会自动推断生成,也可以手动定义 mapping 。GET test/_mapping // 如果没有在创建Index 指定 mapping, es 会通过类型推测创建 mapping{"test" : {"mappings" : {"properties" : {"author" : {"type" : "text", // 一般 string 类型的字段会被动态设别为 text 类型,text 类型会分词"fields" : { // es 支持一个字段多个子类型"keyword" : { // 子类型名为 keyword 查询的时候可以使用 {author.keyword: xxx}"type" : "keyword", // keyword 类型就是 string 类型,但是不会进行分词"ignore_above" : 256 // 默认生成的 keyword 子字段只保留主字段内容的前 256 个字符}}},"book_id" : {...}, // 同author"title": {...}, // 同 author"price" : {"type" : "float" // 33.5 自动推断为 浮点 类型},"public" : {"type" : "date" // "1998-03-11" 自动推断为 日期 类型},}}}}}
第二节 elasticsearch 索引内部原理
1. 数据是如何被搜索到的
在传统数据库中,每个字段都只存储单个值,搜索都是建立在某个字段某个值上(尽管有模糊搜索之类的东西,但是也是拿出某个值来匹配)。 而全文检索要求的是,每个单词都能被索引,也就是一个字段可以被多个值索引。例如 {"text": "aaa bbb ccc"},使用 aaa 或 bbb 或ccc 都能索引到 text 这个字段。
对 一个字段多个值 支持的数据结构就是 倒排索引 了
倒排索引包含一个有序列表,列表包含所有文档出现过的不重复个体,称为 term,对于每一个 term,包含了它所有曾出现过文档的列表。
Term | Doc 1 | Doc 2 | Doc 3 | ...------------------------------------brown | ✔ | | ✔ | ...fox | ✔ | ✔ | ✔ | ...quick | ✔ | ✔ | | ...the | ✔ | | ✔ | ...
当讨论倒排索引时,大家会认为只有在 text 这种分词的长字符串字段才使用倒排索引,事实上,在文档中, 每个被索引的字段都有自己的倒排索引。
2. 索引是不可变的
后面讲 **FST** 会解释这个不可变的原因,下面从官方文档看看它的优缺点。
不变性优点如下:
- 不需要锁。如果你从来不更新索引,你就不需要担心多进程同时修改数据的问题。
- 一旦索引被读入内核的文件系统缓存,便会留在哪里,由于其不变性。只要文件系统缓存中还有足够的空间,那么大部分读请求会直接请求内存,而不会命中磁盘。这提供了很大的性能提升。
- 其它缓存 (像filter缓存),在索引的生命周期内始终有效。它们不需要在每次数据改变时被重建,因为数据不会变化。
- 写入单个大的倒排索引允许数据被压缩,减少磁盘 I/O 和 需要被缓存到内存的索引的使用量。
缺点:
- 因为不可变性,不能修改,如果想要让一个新的文档 可被搜索,你需要重建整个索引。
- 无法直接执行删除操作,只能通过一个 .del 文件标记删除,在合并索引的时候才能真正删除
- 更新操作转换为 删除 -> 创建 。
解决上面确定最简单的方法,就是建立更多的索引,通过增加新的补充索引来反映新近的修改,而不是直接重写整个倒排索引。每一个倒排索引都会被轮流查询到,查询完后再对结果进行合并。
3. 搜索是近实时的
在 Lucence 中,一个 index(索引) 包含了多个可以被搜索的 segment (段),上面说的倒排索引,就是一个个的 segment 。
在 Elasticsearch 中,写入和打开一个 segment 的轻量的过程叫做 refresh 。 默认情况下每个分片会每 1s 自动刷新一次。这就是为什么我们说 Elasticsearch 是 近 实时搜索: 文档的变化并不是立即对搜索可见,但会在一秒之内变为可见。
这些行为可能会对新用户造成困惑: 他们索引了一个文档然后尝试搜索它,但却没有搜到。这个问题的解决办法是用
refreshAPI 执行一次手动刷新:
在每次 refresh 的时候,会写入一个新 segment ,创建新的 segment 和提供搜索虽然很快,但是过多的 segment 会占用很多系统资源,导致 cpu ,文件句柄不足。
4. segment 合并
由于自动 refresh 每秒会创建一个新的段 ,这样会导致短时间内的段数量暴增。而段数目太多会带来较大的麻烦。 每一个段都会消耗文件句柄、内存和cpu运行周期。更重要的是,每个搜索请求都必须轮流检查每个段;所以段越多,搜索也就越慢。
Elasticsearch通过在后台进行段合并来解决这个问题。小的段被合并到大的段,然后这些大的段再被合并到更大的段。
第三节 Lucene 是如何搜索数据的
前文说到了倒排索引,让我们用几条数据来模拟一下倒排索引的存储情况。
| Doc_Id | Name | Age | Sex |
|---|---|---|---|
| 1 | Kate | 24 | Female |
| 2 | John | 24 | Male |
| 3 | Bill | 29 | Male |
当插入这 3 条数据以后,除去 Doc_Id 有3个常规字段,lucene 会创建 3 个倒排索引,如下:
Name 字段的倒排索引:
| Term | Posting List |
|---|---|
| Kate | 1 |
| Join | 2 |
| Bill | 3 |
Age 字段的倒排索引:
| Term | Posting List |
|---|---|
| 24 | 1, 2 |
| 29 | 2 |
Sex 字段的倒排索引:
| Term | Posting List |
|---|---|
| Female | 1 |
| Male | 2, 3 |
可见为每个 field 都建立了一个倒排索引。其中 **Posting list** 就是一个 int 的数组,存储了所有符合某个term的文档 doc_id。当我们的 term 很多的时候,比如:
Carla, Sara, Elin, Ada, Patty, Kate, Selena
如果按照这样的顺序排列,找出某个特定的 term 一定很慢,因为 term 没有排序,需要全部过滤一遍才能找出特定的 term。排序之后就变成了:
Ada,Carla,Elin,Kate,Patty,Sara,Selena
这样我们可以用二分查找的方式,比全遍历更快地找出目标的 term。这个就是 term dictionary。有了 term dictionary 之后,可以用 logN 次磁盘查找得到目标。但是磁盘的随机读操作仍然是非常昂贵的(一次 random access 大概需要 10ms 的时间)。所以为了尽量少的读磁盘,可以把一些数据缓存到 内存里。但是整个 term dictionary 本身又太大了,无法完整地放到内存里。于是就有了 term index。它相当于一个字典,输入 term,得到 term dictionary 的位置,再获取倒排数组 。从从 lucene4开始,为了方便实现前缀,后缀等复杂的查询语句,lucene使用 FST 数据结构来实现 term index。由于使用 FST 实现的 term index 非常小,可以常驻在内存中,这让搜索变得非常快。<br />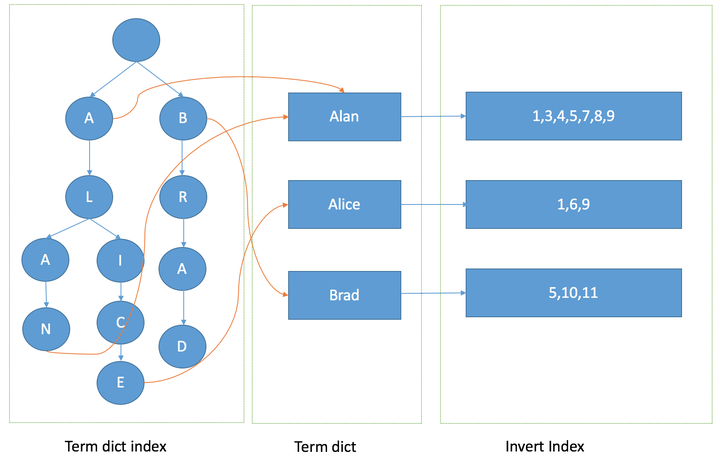 上面这张图就表示 lucene 索引的过程,先从 term index 中获取 term dictionary 磁盘中的地址,然后取出 term dictionary 地址内容中的 Posting list (倒排索引) 指针。最后,lucene 为了高效搜索使用非常多的数据结构和算法,包括不限于下:
- Term index: FST (Finite State Transducers 有限状态传感器)
- 倒排索引列表合并: skip list(跳表), bitset(位数组)
- 范围搜索:BKDTree (一种支持多维数据的搜索树,很复杂)
- 排序:DocValues(列式存储)
第四节 什么是 FST(Finite State Transducers 有限状态传感器)
1. 有限状态机(finite state machine 缩写为 FSM)
要了解 FST ,我们要从它最开始的形态,FSM(finite state machine 有限状态机)说起,FSM 是表示 有限个 状态以及在这些状态之间的 转移 和动作等行为,其中有一个 开始状态 ,零个或者多个 最终状态 ,一次只能处于一个状态。

有限状态机是相当普遍的,可以用来对许多过程建模。上图是一只 **猫咪** 一天的生活,猫只能处于**睡觉**,**玩耍**,**吃饭**,**躲避**,**小盒子内** 5种状态中的一种。其中从一种状态转换到另一种状态需要给定单个输入,例如,猫在**睡觉**,但是只要**提供了食物**(听到晚饭铃),它就会去吃饭,或者**听到什么动静**,他就会醒来去**玩耍** 。猫咪有限状态机可以对给定输入序列进行转换,例如
- 提供食物
- 巨响
- 安静下来
- 消化食物
如果把这些输入应用到上面的状态机,那么 猫咪 的将依次进入以下状态: 睡觉、吃东西、躲起来、吃东西、在垃圾箱中。因此,如果猫咪观察到食物端上来,接着是一声巨响,接着安静下来,最后是 猫咪 在消化食物,那么我们可以得出结论,猫咪此时在猫厕里。
2. 确定性非循环有限状态接受器 (deterministic acyclic finite state acceptor 缩写为 FSA)
一个**确定性的非循环有限状态接受器**是这样一个有限状态机:
- 确定性。这意味着在任何给定的状态下,对于任何输入最多有一个路径可以被选择。
- 非循环。不能访问一个已经访问过的状态,也就是访问路径不能形成环。
一个接受器。有限状态机接受特定的输入序列直到最终状态(以双圈表示)。
下面用 FSA 来实现 **集合** 这个数据结构。假设有一个键为 jul,FSA 是这样的:

第一种情况,如果我们要向 FSA 查询包 **jul** 键,会发生什么情况? 我们需要按顺序处理字符:
- 输入 j,FSA 从开始状态0转换到状态1。
- 输入 u,FSA 从0转换到2。
输入 l,FSA 从2转换到3。
由于键包含的所有字符都已输入 **FSA**,我们现在可以问:**FSA**目前是否处于最终状态? 是的(请注意**状态3**以双圈表示),因此我们可以说 **jul** 在集合中。第二种情况,当我们测试查询不在集合中的键时会发生什么。例如,jun:
输入 j,FSA 从开始状态0转换到状态1。
- 输入 u,FSA 从0转换到2。
输入 n,FSA 无法转换状态,程序结束。
FSA 不能继续移动了,因为 **状态2** 之外的唯一路径是 l,但当前输入是 n。由于 l 不等于n, **FSA** 不能进入该路径。一旦 **FSA** 在给定的输入下不能移动,它就可以断定键不在集合中。无需进一步处理输入。第三种情况,查询另一个键 **ju**:
输入 j,FSA 从开始状态0转换到状态1。
输入 u,FSA 从0转换到2。
在这种情况下,整个输入已经结束,并且 **FSA ** 处于 **状态2**。要确定 ju 是否在集合中,它必须询问 **状态2** 是否为最终状态。 由于不是,它可以报告 ju 键不在集合中。从上面三种情况可以看出,确认一个键是否在集合中所需要的步骤数量是由键中的字符数量决定的!也就是说,查找键花费的时间与集合的大小完全无关。查询的时间复杂度是 **O(K)**,K 为字符串的长度。
3. Trie 前缀树
一个 **trie** 可以被认为是一个特殊的 **FSA** ,它只共享键的前缀,而 **FSA** 除了共享前缀,也共享后缀(第4节会谈到)。我们看看一个插入了 **mon** , **tues** , **thurs** 的集合对应的 **trie** 长什么样子。从图中可以看出,我们用 **状态0** 到 **状态4** 这一个路径,表示了 **tues** , **thurs** 共同的前缀 **t** 。**trie** 的查询和上节的 **FSA** 查询一样。在聊 **FSA** 的构建之前,我们先说说 **trie** 的构建,因为只共享前缀的 **trie** 构建相当简单。给定要插入的新键,执行常规查找即可。如果输入已用尽,则当前状态应标记为终结状态(图中的双层圆圈)表示 。如果机器在输入时没有后续的可用路径,那么只需为每个剩余的输入创建一个新的路径和状态,创建的最后一个状态应该标记为最终状态即可。
4. FSA 的构建
上文说到,**trie** 和 **FSA** 的唯一区别是 FSA 允许在键之间共享后缀。因为这个区别, **trie** 通常比 **FSA** 大得多。由于 **trie** 本身就是一个**FSA**,我们可以构造一个 **trie**,然后应用一些有限状态机通用的最小化算法(DFA minimization 将有限状态机转换为具有最少状态数的算法),就能实现我们共享后缀的目标。不过通用的最小化算法 在时间和空间上都非常昂贵。其中一种实现就是,做一个状态哈希表,将所有状态都作为一个哈希的键,然后遍历整个有限状态机,消除重复的状态,但是这是一个指数级的算法。最关键的一点来了,如果我们假设 **键是有序的**,那就可以大幅度减少算法的复杂度。诀窍在于:在插入新键时,可以冻结 **FSA** 中未与新键共享前缀的任何部分。但是任何添加到 FSA 的新键都不可能使 FSA 变得更小。下面的一系列图片会更好的帮助我们理解。依次插入 **mon**,**tues** 和 **thurs**。由于我们必须按字符串大小的顺序添加它们,因此,我们先添加 **mon**,然后再添加 **thur**,最后再添加 **tues**。 添加第一个键后,FSA的情况如下:

很简单的情况。但是当我们插入 thurs 时,会发生以下情况:

插入 thur 会导致第一个键 **mon** 冻结(图中蓝色圆圈)。当 **FSA** 的特定部分被冻结时,我们知道以后将不再需要对冻结的状态进行修改。也就是说,由于后续所有待添加的键都大于等于 thurs,所以后面没有键再以 mon 开头。这很重要,因为它使我们可以重用自动机的该部分,而不必担心将来是否会更改。 换句话说,颜色为蓝色的状态可供其他键重用。虚线表示 **Thur** 尚未真正地添加到 **FSA** 中。因为添加它需要检查是否存在任何冗余的状态。 不过我们还不能做到这一点。例如,**状态3** 和 **状态8** 确实是等效的:两者都是最终状态,并且都没有任何后续路径。但是,状态8并不能肯定后续也等于**状态3**。例如,我们添加的下一个键可能是 **thursday**。这会将**状态8**后有一个 **d** 的路径,这将使其不等于**状态3**。因此,我们还不能完全得出结论,**thurs** 在自动机中是什么样子。让我们继续插入下一个键,**tues**

在添加 **tues** 的过程中,我们推断出 **thurs** 的 **hurs** 部分是可以被冻结的。为什么? 因为未来插入的任何键都不可能减少 **hurs** 所采取的路径,因为键是按字符串顺序插入的。例如,我们现在知道键 **thursday** 永远不可能存在集合中,因为 **thursday** 小于 **tues**。所以我们可以得出结论,**thurs** 的最终状态等同于 **mon** 的最终状态,可以重用**状态3**。请注意,**状态4** 仍然是虚线: 随后插入键时,**状态4**可能会发生变化,因此还不能认为它与其他任何状态相同。让我们再插入一个键,可以更清晰上面的流程,插入 **zon** 。

我们在这里看到**状态4**终于被冻结了,因为以后在 **zon** 之后的键插入都不可能改变 **状态4**。此外,我们还可以得出结论,**thurs** 和 **tues** 有一个共同的后缀,实际上,**状态7**和**状态9**(上面一张图)是等价的,都有一个相同 **s 路径**的状态 。最重要的是,它们的两个 **s 路径 **后续的状态都是**相同的状态**,否则我们就不能重用**状态**。最后,我们必须发出插入键结束的信号。我们现在可以冻结**FSA**的最后一部分**zon**,并寻找最后的冗余结构。

当然,由于 **mon** 和 **zon** 具有相同的后缀,因此确实存在多余的结构。也就是说,上一张图中的**状态9**在各方面都与**状态1**等价。这是正确的,因为**状态10**和**11**也与**状态2**和**3**等价。如果条件不成立,则我们不能认为**状态9**和**1**相等。例如,如果我们将 **mon** 插入到我们的集合中,并且仍然假设状态9和状态1相等,那么生成的 FSA 将看起来像这样:

这将是错误的!为什么?因为**FSA**会声称 **zom** 在集合中,但是我们从来没有添加它。最后,值得注意的是,此处概述的构造算法可以在 **O(n)** 时间内运行,其中 **n** 是键的数量。 不难发现,假设在每种状态下查找路径要花费固定的时间,则在不检查**冗余结构**的情况下,将键插入 **FSA** 所花费的时间不会比循环遍历键中的每个字符花费的时间长。但是还有更棘手的是:我们如何在恒定时间内找到**冗余结构**? 简短的答案是一个**哈希表**,后面我还会再详细说一下实现的细节。
5. FST 构建
**FSA** 能帮我们构建一个集合,但是用来做索引还是有点困难,因为不止需要判断键是否存在,我们还需要知道,如果索引的键存在,它背后的数据是什么。所以我们需要的是一个 **映射表(字典)**,通常有序的**映射表**都是使用**二分搜索树**或 **btree** 实现的,无序的**映射表**使用**散列表**实现。在本节中,我们通过增强 **FSA** 来实现**映射表**。这种增强的 **FSA** 称为 **确定性非循环有限状态转换器(deterministic acyclic finite state transducer 缩写为FST)**。一个 **FST** 是这样一个有限状态机 (前两个标准与 **FSA** 相同)。
- 确定性。这意味着在任何给定的状态下,对于任何输入最多有一个路径可以被选择。
- 非循环。不能访问一个已经访问过的状态,也就是访问路径不能形成环。
一个转换器。有限状态机产生一个与特定输入序列相关联的值。当且仅当输入序列导致状态机处于最终状态时才会获得对应的值。
换句话说,**FST** 就像 **FSA**, 只是除了回答建是否存在外, **FST** 还会给出与键对应的值。**FSA** 表示一个集合只需要在状态机的转换路径中存储键就可以了。但是映射需要做的不仅仅是“接受”输入序列。 它还需要返回与该键关联的值。将值与键关联的一种方法是向每个路径附加一些数据。就像使用输入字符将状态机从一个状态移动到另一个状态一样,可以在状态机从一个状态移动到另一个状态时顺带生成一些值。这种额外的能力使状态机成为一个转换器。让我们看一个映射的例子,其中有一个元素 **jul**,它与值 **7** 相关联:

此状态机与对应的集合相似,不同之处在于第一个路径 **j** 从0到1的转换有附加输出**7**。其他的路径,u 和 l,也有一个与它们相关的输出**0**,在图像中省略了。与集合一样,我们可以查询字典是否包含键 **jul**。但是我们还需要返回关联值。以下演示了状态机如何处理寻找键 **jul**:
- 初始值 value 为 0
- 输入 j, FST 从状态0转换到状态1. value 值加7
- 输入 u, FST 从状态1转换到状态2. value 值加0
输入 l, FST 从状态2转换到状态3. value 值加0
由于 FST 输入已经结束,因此我们现在可以问:FST是否处于最终状态? 是的,所以我们知道 jul 在映射中。此外,我们可以得到键 jul 关联值7。我们将复用前一节中的示例和键 **mon**、**tues** 和**thurs**。因为 **FST** 是一个**映射表**,所以我们将把其在每周对应的天数与每个键关联起来:2、3和5。
与前面一样,我们将首先插入第一个键 mon

(请记住,虚线对应的 FST 的片段可能在随后插入新键时发生变化)
这并非很有趣,但值得注意的是 输出2 被放置在第一个路径上。从技术上讲,下面的转换器同样是正确的

然而,将关联值放在尽可能接近初始状态的位置,这能使编写一个在键之间共享转换路径的算法变得更加容易。
让我们继续插入键 thurs 及其关联值 5 到映射中

与 FSA 结构一样,插入 thurs 可以让我们得出这样的结论: FST 的 mon 部分永远不会改变。(如图中蓝色所示。)
由于 mon 和 thurs 没有公共前缀,而且它们是映射中仅有的两个键,所以它们的整个输出值都可以放在开始状态之外的第一个路径中。
但是,当我们添加下一个键 tues 时,事情就变得更有趣了

与 **FSA** 结果一样,插入一个新的键会冻结 **FST** 的另一部分。此处的区别在于,从**状态0**到**4**的路径上的输出已从 **5** 变为 **3** 。这是因为 **tues** 键的关联值为 **3**,所以如果初始路径 **t** 将 **5** 加到该值,则会造成 **tues** 整个路径的值过大。我们希望共享尽可能多的结构,因此当我们确定一个公共前缀时,我们也在关联值中寻找该公共前缀。在这种情况下,前缀 **5** 和 **3** 为 **3** 。由于 **3** 是与键 **tues** 相关联的值,因此其剩余的路径关联值都应为0。但是,如果我们将状态 **0->4** 的输出从 **5** 变为 **3**,那么与键 **thurs** 相关联的值现在就错了。所以我们要把 **5** 和 **3** 的前缀放置位置向后推。在本例中,**5 - 3 = 2**,因此我们在 **状态4** 之后的路径上添加 **输出2** (**路径u** 不用添加)。用这个方法,我们可以保留先前键的关联值,为新键添加新的关联值,并在FST中共享尽可能多的结构。与前面一样,让我们尝试再添加一个键。这一次,让我们选择一个对输出有更有趣影响的键。让我们将 **tye** 添加到映射中,并将其与**值99**关联起来,看看会发生什么。
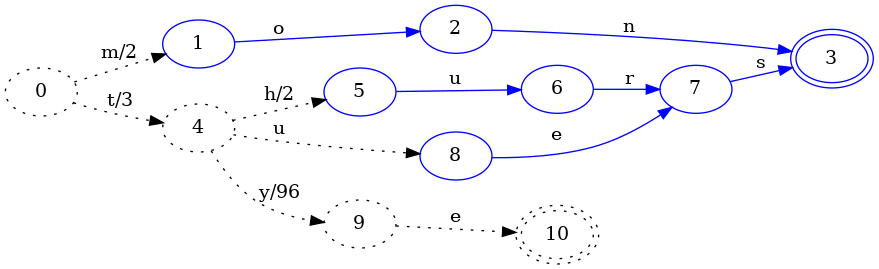
插入 **tye** 让我们可以冻结 **tues** 中 **es** 的部分。特别是,与 **FSA** 构建一样,我们确定了等价状态,以便 **thurs** 和 **tues** 可以共享 **FST** 中的状态。这里与前面的构造的不同之处在于,与**4->9**路径(刚刚为 **tye** 添加)关联值为**96**。选择**96**是因为在它之前的路径,**0->4**,输出是**3**。因为**99**和**3**的公共前缀是**3**,所以 **0->4** 的关联值保持不变,而 **4->9** 的关联值设置为**99 - 3 = 96**。
为了完整起见,以下是 FST 的最终状态,不再添加任何键。
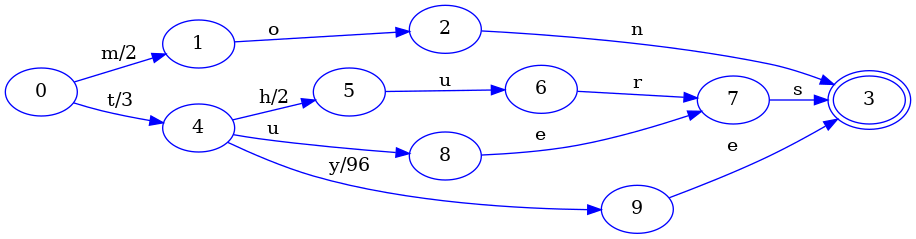
与上一步相比,这里唯一真正的变化是,tye 与所有其他键共享最终状态。
上文描述关联值类型可能有点限制; 如果它们不是整数呢? 实际上,可以在 FST 中使用的关联值类型含有如下操作的接口:
- 加(Addition)
- 减 (Subtraction)
- 取前缀 (对于整数来说,就是min)
关联值的类型 I 也必须满足一个附加的接口定义,这样,保证下列定律成立。
- x + I = x 例如 int + int = int
- x - I = x 例如 int - int = int
prefix(x, y) = I,当 x 和 y 共享前缀时 例如 min(int, int) = int
整形(int)一般满足这个接口定义 (其中前缀定义为 min ),附加的好处是它们非常小。也可以使用其他类型来满足这个代数定律,只要这个类型能满足以上接口。我们只需要在上面的例子中使用加法,但是我们需要另外两个操作来构建 FST。这就是我们接下来要讲的。
6. 实践中的构建
上图是从一张用各种算法构建英文词汇表的图,其中可以看到 **紫色** 的线条就是 **trie** 的构建,内存占用和词汇数量成正比,所以想在内存中构建一个存储大量键的 **trie** 显得非常困难,而 **FST** 是 **trie** 的拓展加强版,如果使用通常的做法,那也会占用特别高的内存。**FST** 数据结构的关键应用场所之一是其**存储**和**搜索**大量键的能力。这个目标与上面描述的算法有些不一致,因为它为了检测 FST 的某些部分是否为通用的后缀,您必须能够搜索实际这个后缀的状态,也就是需要将所有**冻结状态** 保存在内存中。如果有一个方法是让**冻结**的状态节点先写入磁盘,而不是保持则内存中,则可以大幅降低内存的消耗。原文作者提到 **FST** 相关的论文指出可以使用哈希表存储**冻结状态**,哈希表提供对任何特定状态的**恒定时间**访问(假设哈希函数良好)。这种方法的问题在于,除了将所有状态实际存储在内存中的哈希表中,也会产生巨大的内存开销。但是我们可以通过牺牲生成的 **FST** 最小化保证,可以减少所需的内存。即,可以维护一个有大小限制的哈希表。这意味着常用的状态保留在哈希表中,而不太常用的状态则被剔除。实际上,在原文作者不科学的实验中,具有约10,000个插槽的哈希表可以达到不错的折中效果,并且非常接近最小值。使用仅存储部分状态的有限哈希表的一个有趣结果是,可以将 **FST** 的构造**流式写入**磁盘上的文件中。也就是说,在构建 **FST** 时,当状态被冻结时,状态节点可以不保存在内存中。而是立即将它们写入磁盘(或套接字,或其他任何东西)。最终结果是,**我们可以在线性时间和恒定内存中根据预排序的键构造一个最小的 FST**。
7. 内存
在 **FST** 构建完以后,查询单个单词是很快的,但是在触发查询前,有一个非常昂贵的操作,就是需要将所有查询字段在磁盘中 **FST** 文件加载到内存并反序列化,这显然非常耗费时间和内存,如果读入内存后不驱除,迟早会写满内存。解决这种情况的一种可能方法是让 **FST** 数据结构如何直接从文件中读取。特别是,它可以发出`seek`系统调用以在文件中跳转以遍历有限状态机。但是磁盘随机寻址相对内存寻址是非常慢的,而`seek` 调用会非常频繁地发生。每个`seek`都需要系统调用的开销,这可能会使搜索 **FST** 的速度慢得令人望而却步。另一种解决的方法是维护一个大小有限的缓存并将文件的块存储在内存中,但可能不是全部。当需要访问不在缓存中的文件区域时,会读取包含该区域的文件块并将其添加到缓存中(可能会驱逐一段时间未访问的块)。当我们再次访问该区域并且它已经在缓存中时,则不需要 I/O。这种方法还使我们能够聪明地了解内存中存储的内容。也就是说,我们可以确保接近 **FST** 初始状态的所有块都在缓存中,因为理论上这些块是最常访问的。不幸的是,这种方法实现起来非常复杂。第三种方式称为 [内存映射文件](https://zh.wikipedia.org/wiki/%E5%86%85%E5%AD%98%E6%98%A0%E5%B0%84%E6%96%87%E4%BB%B6) (mmap)。创建内存映射文件时,它对我们来就好像它是内存中的字节序列。当我们访问该内存区域时,可能还没有要读取的文件中的实际数据。这会导致 _page fault_ (页面错误),这个错误会告诉操作系统从文件中读取一个块,并使其可用于暴露给程序的字节序列。然后操作系统负责文件的哪些部分实际上在内存中。从文件中读取数据并将其存储在内存中的实际过程对我们的程序是透明的。第三种方式实际上与我们上面使用缓存的想法非常相似。关键的区别在于操作系统而不是我们来管理缓存。这是实现起来会轻松很多。当然,也有一些成本。由于操作系统管理缓存,它无法知道 **FST** 的某些部分应该始终留在内存中。因此,有时我们可能没有最佳查询时间。这里还有一个值得一提的成本。用于在内存中表示 **FST** 的格式会导致数据的随机访问。也就是说,查找一个键可能会跳转到 **FST** 的不同区域,这些区域根本不相互靠近。这意味着通过内存映射从磁盘读取 **FST** 消耗的资源可能很昂贵,因为磁盘随机访问 **I/O** 很慢。尤其是非固态磁盘时,因为磁盘随机访问将需要大量物理搜索。如果您发现自己处于这种情况并且操作系统的页面缓存无法补偿,那么您可能需要先花费一点时间将整个 FST 加载到内存中。这并不是一件不可能的事情,因为 FST 的非常小。例如,具有数百万个密钥的 FST 只耗费几兆字节的内存。
第五节 相关代码库
SimpleFst (笔者根据文章概念使用 Python 编写的简易 FST)
fst (Index 1,600,000,000 Keys with Automata and Rust 的作者使用 Rust 实现的完整版 FST,功能非常强大丰富)
vellum (Go 语言实现的完整版 FST,功能基本和 fst 差不多)
mafsa (GO 语言实现的 FSA , 功能较为简单,代码简洁易读,笔者从中吸取了很多经验)
dafsa (Python 实现,文章中提到的使用 Trie + 通用最小化算法 的 FSA)
FSTCompiler.java (Lucene 中 FST 的 java 实现)
引用文献
Index 1,600,000,000 Keys with Automata and Rust

