2015-09-15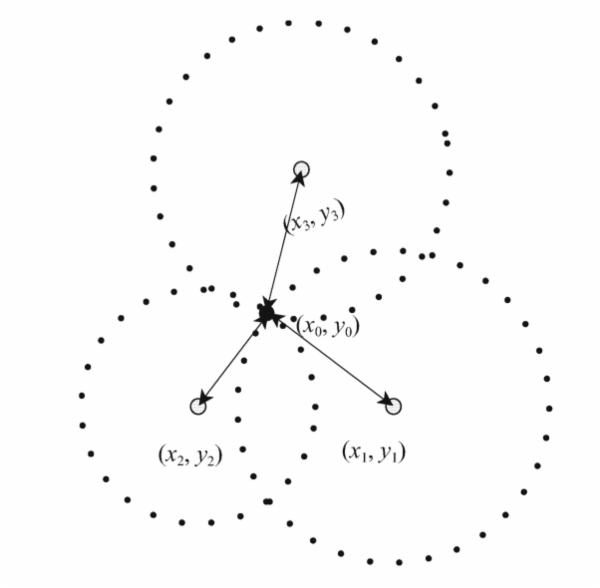
基本原理**
Trilateration（三边测量）是一种常用的定位算法：
- 已知三点位置 (x1, y1), (x2, y2), (x3, y3)
- 已知未知点 (x0, y0) 到三点距离 d1, d2, d3
以 d1, d2, d3 为半径作三个圆，根据毕达哥拉斯定理，得出交点即未知点的位置计算公式：
( x1 - x0 )2 + ( y1 - y0 )2 = d12( x2 - x0 )2 + ( y2 - y0 )2 = d22( x3 - x0 )2 + ( y3 - y0 )2 = d32
解法推导
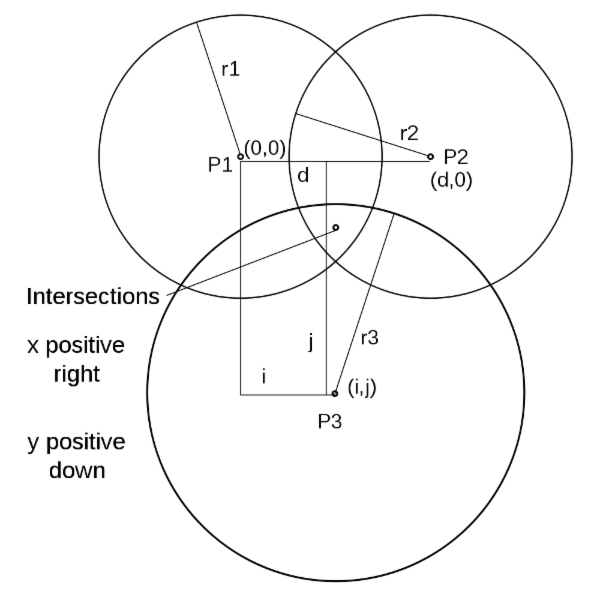
设未知点位置为 (x, y)， 令其中的第一个球形 P1 的球心坐标为 (0, 0)，P2 处于相同纵坐标，球心坐标为 (d, 0)，P3 球心坐标为 (i, j)，三个球形半径分别为 r1, r2, r3，z为三球形相交点与水平面高度。则有：
r12 = x2 + y2 + z2r22 = (x - d)2 + y2 + z2r32 = (x - i)2 + (y - j)2 + z2
当 z = 0 时， 即为三个圆在水平面上相交为一点，首先解出 x:
x = (r12 - r22 + d2) / 2d
将公式二变形，将公式一的 z2 代入公式二，再代入公式三得到 y 的计算公式：
y = (r12 - r32 - x2 + (x - i)2 + j2) / 2j
D3.js实现
定义三个圆的坐标及半径，计算出交点的坐标 (obj_x, obj_y).
var x_0 = 150, y_0 = 150;var x_1 = x_0, y_1 = y_0, d = 150, x_2 = x_0 + d, x_3 = 225, y_3 = 315, r = 100;var i = x_3 - x_0, j = y_3 - y_0;var x = (Math.pow(r, 2) - Math.pow(r, 2) + Math.pow(d, 2)) / (2 d) + x_0;var obj_x = x + x_0;var y = (Math.pow(r, 2) - Math.pow(r, 2) - Math.pow(x, 2) + Math.pow((x - i), 2) + Math.pow(j, 2)) / (2 j);var obj_y = y + y_0;
绘出圆形及交点：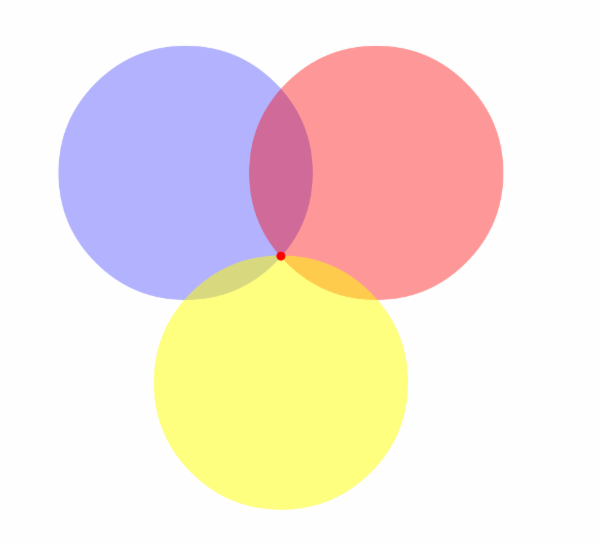
svg.append(“circle”).attr(“cx”, x_1) .attr(“cy”, y_1).attr(“r”, r) .style(“fill”, “blue”).style(“opacity”, 0.3);svg.append(“circle”).attr(“cx”, x_2) .attr(“cy”, y_0).attr(“r”, r) .style(“fill”, “red”).style(“opacity”, 0.4);svg.append(“circle”).attr(“cx”, x_3) .attr(“cy”, y_3).style(“opacity”, 0.5) .attr(“r”, r).style(“fill”, “yellow”);svg.append(“circle”).attr(“cx”, obj_x) .attr(“cy”, obj_y).attr(“r”, 3) .style(“fill”, “red”);
但在实际定位中，给定的距离由于测量的误差，并不能真正让三个圆交于一点，需要在相交区域绘制出矩形并计算矩形的中心位置，除三边测量计算公式之 外，也许还可以采用K-Means或Overlap聚类算法，后两者在地图标注上使用比较广，有兴趣的可以进一步对定位算法进行研究。
若有收获，就点个赞吧
0 人点赞
