朴素贝叶斯

一.朴素贝叶斯算法的基本概念、核心思想

首先我们来讨论一下朴素贝叶斯算法里面涉及到的几个核心概念：先验概率、后验概率、联合概率、全概率公式、贝叶斯公式。
是不是看到上面这么多概念有点懵，不着急。让我们根据一个买西瓜的小故事，来论述这几个概念，从而对上述概念有一个直观且深刻的理解。
想象这样一个场景，在一个炎热夏天的午后，我们想整个又大又甜的西瓜来清爽一下。于是我们一路小跑的来到超市，到超市以后我们需要选一个又大又甜的西瓜。我们根据常识或是经验知道放在超市里面卖的西瓜，一般情况下是熟的，假设根据统计，在超市里面卖的西瓜成熟的概率是70%，这个概率就是先验概率，先验概率（prior probability）就是根据以往经验和分析得到的概率。因为是西瓜成熟的概率是70%，所以还是有30%的西瓜没有熟，所以我们还是需要好好的挑一挑。那我们根据什么选择呢?作为一个吃货，我有些经验，比如瓜蒂脱落的话，西瓜成熟的概率会更高，大概是 85%。如果把瓜蒂脱落当作一种已有的结果，然后去推测西瓜成熟的概率，这个概率 P(瓜熟|瓜蒂脱落) 就被称为后验概率。后验概率类似于条件概率。
明白了先验概率和后验概率，我们再来认识一下联合概率。在买西瓜的例子中，P(瓜熟，瓜蒂脱落) 就是联合概率，它表示瓜熟了且瓜蒂脱落的概率。关于联合概率，满足下列乘法等式：

其中，P(瓜熟|瓜蒂脱落) 就是刚刚介绍的后验概率，表示在“瓜蒂脱落”的条件下，“瓜熟”的概率。P(瓜蒂脱落|瓜熟) 表示在“瓜熟”的情况下，“瓜蒂脱落”的概率。
接着，我们想如何计算瓜蒂脱落的概率呢？瓜蒂脱落可以分成两种情况：一种是瓜熟状态下瓜蒂脱落的概率，另一种是瓜生状态下瓜蒂脱落的概率。瓜蒂脱落的概率就是这两种情况之和。因此，我们就推导出了全概率公式：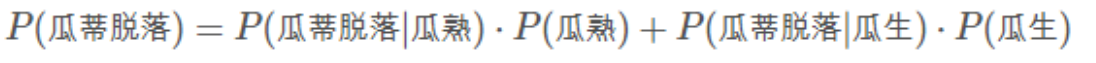

介绍完先验概率、后验概率、联合概率、全概率后，我们来看这样一个问题：西瓜的状态分成两种：瓜熟与瓜生，概率分别为0.7与0.3，且瓜熟里面瓜蒂脱落的概率是0.8，瓜生里面瓜蒂脱落的概率是0.4。那么，如果我现在挑到了一个瓜蒂脱落的瓜，则该瓜是好瓜的概率多大？
显然，这是一个计算后验概率的问题，根据我们上面推导的联合概率和全概率公式，可以求出：

上面的公式就是我们的贝叶斯公式，我们一项项来分析：
条件概率 P(瓜蒂脱落|瓜熟) = 0.8
先验概率 P(瓜熟) = 0.7
条件概率 P(瓜蒂脱落|瓜生) = 0.4
先验概率 P(瓜生) = 0.3
将以上数值带入上式，得：
P(瓜熟|瓜蒂脱落) = 0.80.7 / （0.80.7 + 0.40.3）
这样，我们就计算得到了瓜蒂脱落的瓜是好瓜的概率为 0.82。以上这种计算后验概率的公式就是利用贝叶斯定理。有点意外吧？不知不觉，可以说你已经掌握了贝叶斯定理的思想了。
我们在上面判断西瓜是否成熟只用了一个特征：瓜蒂脱落，实际上瓜的成熟还与其他特征有关，比如看瓜的形状和颜色。形状有圆和尖之分，颜色有深绿、浅绿、青色之分。要看这么多特征啊？不用担心，跟我们上面使用瓜蒂脱落这一个特征判断西瓜是一样的，我们使用刚刚引入的贝叶斯定理思想来尝试解决这个问题。
现在，特征由原来的 1 个，变成现在的 3 个，我们用 X 表示特征，用 Y 表示瓜的类别（瓜熟还是瓜生）。则根据贝叶斯定理，后验概率 P(Y=ck|X=x) 的表达式为：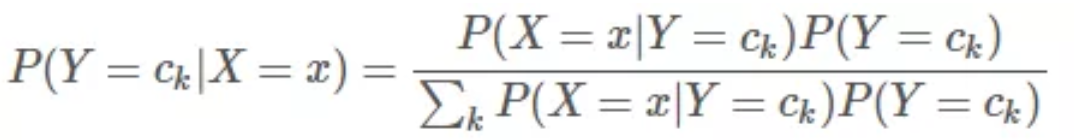

其中，ck 表示类别，k 为类别个数。本例中，k=1，2，c1 表示瓜熟，c2 表示瓜生。上面的公式看似有点复杂，但其实与单特征（瓜蒂是否脱落）的形式是一致的。
有一点需要注意，这里的特征 X 不再是单一的，而是包含了 3 个特征。当特征个数比较多的时候，条件概率 P(X=x|Y=ck) 有指数级数量的参数，其实际估计是不可行的。因此朴素贝叶斯法对条件概率分布做了条件独立性假设。条件独立假设就是说用于分类的特征在类别确定的条件下都是条件独立的，在买瓜这个例子中就代表瓜蒂是否脱落、瓜的形状和颜色对西瓜成熟与否的影响是相互独立的。由于这是一个较强的假设，因此朴素贝叶斯法也由此得名。这样,P(X=x|Y=ck) 就可以写成：
P(X=x|Y=ck) = P(X1=x1, …, Xn=xn|Y=ck) = ΠP(Xj=xj|Y=ck)
其中，n 为特征个数，j 表示当前所属特征。针对买瓜这个例子，P(X=x|Y=ck)可以写成：
P(X=x|Y=ck) = P(X1=x1|Y=ck) P(X2=x2|Y=ck) * P(X3=x3|Y=c3)
这一假设让朴素贝叶斯法变得简单，但是有时候会牺牲一定的分类准确率。这样，利用朴素贝叶斯思想，我们就可以把后验概率写成：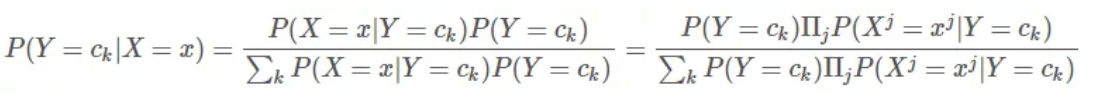

不是说好没有那么多公式的吗？别担心，上面的公式看上去比较复杂，其实只是样本特征增加了，形式上与P(瓜熟|瓜蒂脱落) 是一致的。
现在，我们拿起一个西瓜，观察了它的瓜蒂、形状、颜色三个特征，就能根据上面的朴素贝叶斯公式，分别计算c1（瓜熟）和c2（瓜生）的概率，即P(Y=c1|X=x)和P(Y=c2}|X=x)。然后再比较P(Y=c1|X=x)和P(Y=c2|X=x)值的大小：
若P(Y=c1|X=x) > P(Y=c2|X=x)，则判断瓜熟；
若P(Y=c1|X=x) < P(Y=c2|X=x)，则判断瓜生。
值得注意的是上式中的分母部分，对于所有的 ck 来说，都是一样的。因此，分母可以省略，不同的 ck，仅比较 P(Y=ck|X=x) 的分子即可：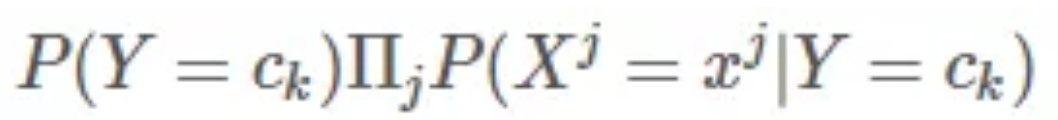

通过上面买瓜的小故事，我们对朴素贝叶斯算法有了一个总体的把握。接下来，我们使用朴素贝叶斯算法完成一个具体的例子，这样我们能够对上述理论知识有一个更深刻的认识。

二.朴素贝叶斯算法的实例

我们在第一节对朴素贝叶斯算法的理论有了一个基本的掌握，接下来我们使用朴素贝叶斯分类器来实际选择西瓜。在使用朴素贝叶斯分类器之前，还有一件事情要做，我们需要收集样本数据。我们通过网上资料和查阅，获得了一组包含 10 组样本的数据。这组数据是不同瓜蒂、形状、颜色对应的西瓜是生是熟。我们把这组数据当成是历史经验数据，以它为标准。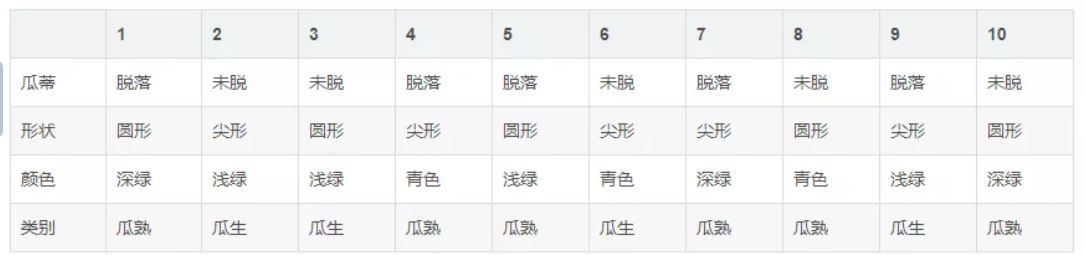

其中，瓜蒂分为脱落和未脱，形状分为圆形和尖形，颜色分为深绿、浅绿、青色。不同特征组合对应着瓜熟或者瓜生。
现在，我们挑了一个西瓜，它的瓜蒂脱落、形状圆形、颜色青色。这时候，我们就完全可以根据样本数据和朴素贝叶斯法来做选择了。
首先，对于瓜熟的情况：
瓜熟的先验概率： P(瓜熟) = 6 / 10 = 0.6。
条件概率： P(脱落 | 瓜熟) = 4 / 6 = 2 / 3。
条件概率： P(圆形 | 瓜熟) = 4 / 6 = 2 / 3。
条件概率： P(青色 | 瓜熟) = 2 / 6 = 1 / 3。
当西瓜是成熟时计算P(Y=ck|X=x)分子部分：
P(瓜熟) × P(脱落 | 瓜熟) × P(圆形 | 瓜熟) × P(青色 | 瓜熟) = 0.6 × (2 / 3) × (2 / 3) × (1 / 3) = 4 / 45。
然后，对于瓜生的情况：
瓜生的先验概率： P(瓜生) = 4 / 10 = 0.4。
条件概率： P(脱落 | 瓜生) = 1 / 4 = 0.25。
条件概率： P(圆形 | 瓜生) = 1 / 4 = 0.25。
条件概率： P(青色 | 瓜生) = 1 / 4 = 0.25。
当西瓜是生的时候计算 P(Y=ck|X=x) 分子部分：
P(瓜生) × P(脱落 | 瓜生) × P(圆形 | 瓜生) × P(青色 | 瓜生) = 0.4 × 0.25 × 0.25 × 0.25 = 1 / 160。
因为 4 / 45 > 1 / 160，所以我们预测为瓜熟。终于计算完了，我们可以很肯定地说这个西瓜瓜蒂脱落、形状圆形、颜色青色，应该是熟瓜。回到家一看，果然瓜熟了。
通过本节选择西瓜的例子，我们应该对朴素贝叶斯算法的理论有了更深刻的认识，并且也能够在实际的场景中应用朴素贝叶斯算法来做分类了。至此我们已经完成了对朴素贝叶斯算法的理论学习和实际应用，最后，让我们来对朴素贝叶斯算法做一个总结。

三.朴素贝叶斯算法的总结

现在我们对朴素贝叶斯算法做一个总结，朴素贝叶斯算法是以贝叶斯公式为核心，在计算条件概率P(X=x|Y=ck)时，由于参数具有指数级的数量，其实际估计是不可行的。因此朴素贝叶斯法对条件概率分布做了条件独立性假设。由于这是一个较强的假设，因此朴素贝叶斯法也由此得名，这就是朴素贝叶斯的核心。

参考文献：

[1]通俗易懂！白话朴素贝叶斯，文章链接：https://mp.weixin.qq.com/s/7xRyZJpXmeB77MZNLqVf3w
[2]统计学习方法2，李航