一、二叉树失衡

之前学习过二叉树，但是二叉树可能会出现极端的情况，此时的二叉树性能会下降

就像下面的二叉树，已经是一个链表了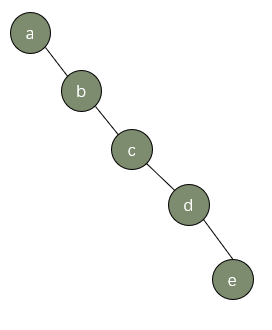
image.png
这种情况就是二叉树的失衡，即左右子树的高度不一样。

二、平衡二叉树

所以，为了解决上述问题，就提出了平衡二叉树的概念。

平衡二叉树的左子树和右子树都是平衡二叉树，并且左子树和右子树的深度之差的绝对值不超过1.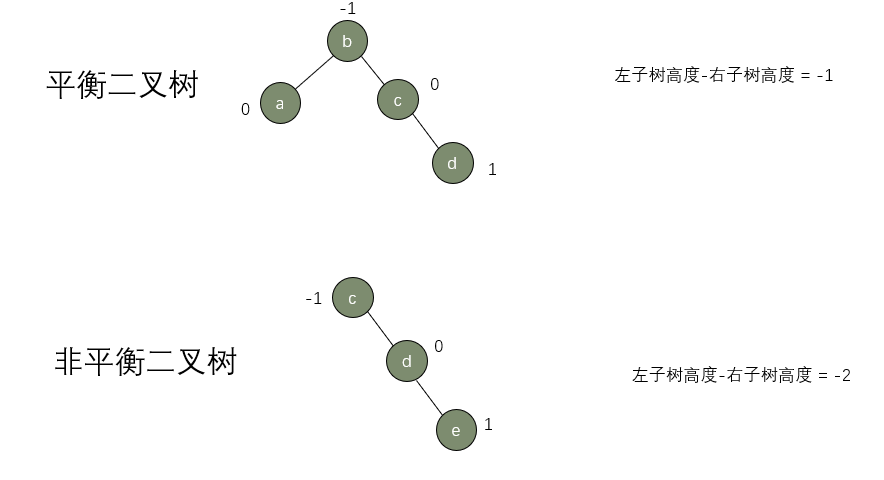
image.png
而平衡二叉树本身的性能在查找方面能够达到O(logn)，因为中序遍历本质上就是二分查找，所以我们要利用平衡二叉树的这个特性，接下来就是想办法将一个非平衡二叉树转成一个平衡二叉树。

三、左旋和右旋是法宝

3.1 左旋

左旋，从意思上来看就是向左旋转。当一个二叉树的右子树高度比左子树高度大于2时，这个树就需要左旋来保持平衡了。

下面这棵树是一个失衡的二叉树，并且第一个失衡的节点已经用红色圈出来（第一个失衡，那么它的父节点也会失衡，但是我们只需要调整第一个失衡节点，剩下的节点也会自动平衡）。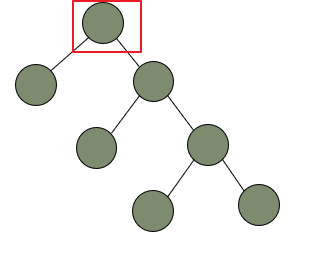
image.png
接下来就需要对上述的失衡二叉树采用左旋的方式进行平衡化，将其中变动的几个节点用颜色标注出来，看一下这几个特殊的节点变化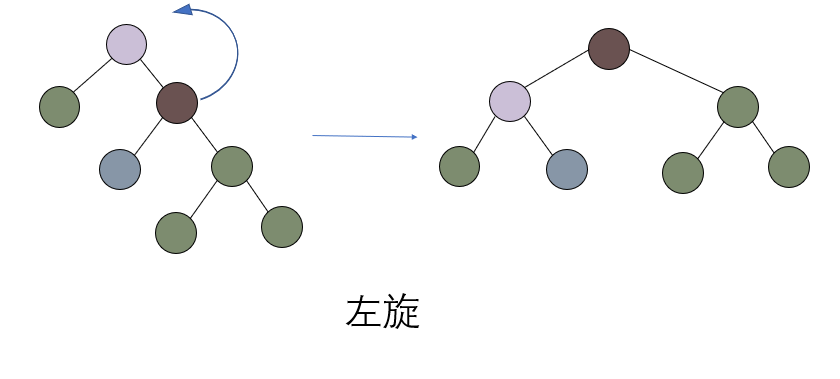
image.png
我们只需要变动上述3个节点就能够把一棵失衡的二叉树给平衡化，多神奇！

3.2 右旋

和左旋相对，如果某个节点的左子树高度比右子树高度大2，那么这棵树就需要进行右旋了，就比如下面这棵树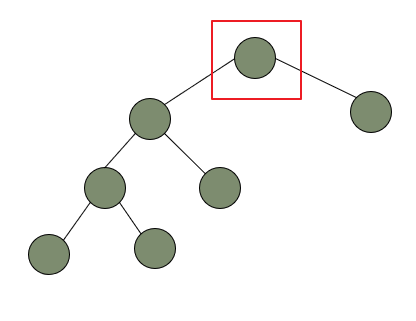
image.png
现在对它进行右旋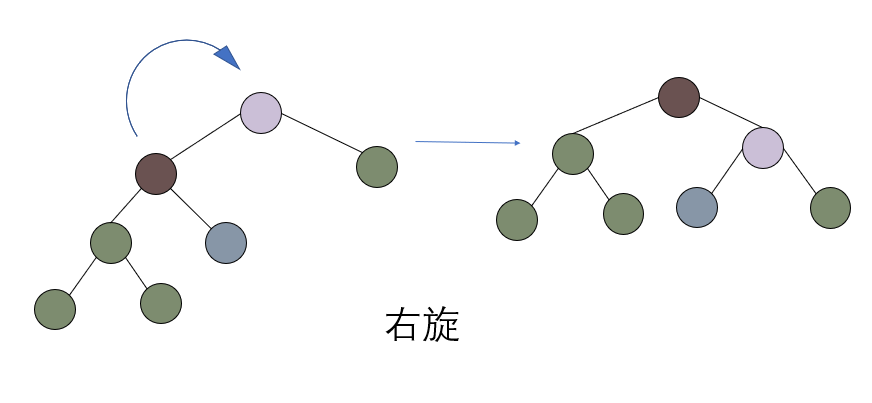
image.png
现在经过右旋，整棵树的高度已经平衡了。

3.3 双旋

单纯左旋不太够

之前学了左旋和右旋，针对失衡二叉树已经有了制胜法宝了。但是，有时候只有一个左旋/右旋是不够的，就比如下面这棵树。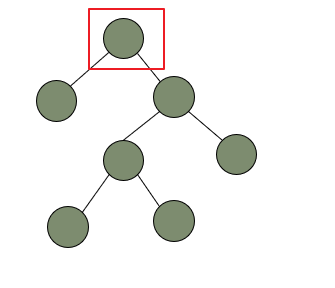
image.png
其右子树高度比左子树高度大2，所以应该采取左旋，接下来我们对它左旋一次看看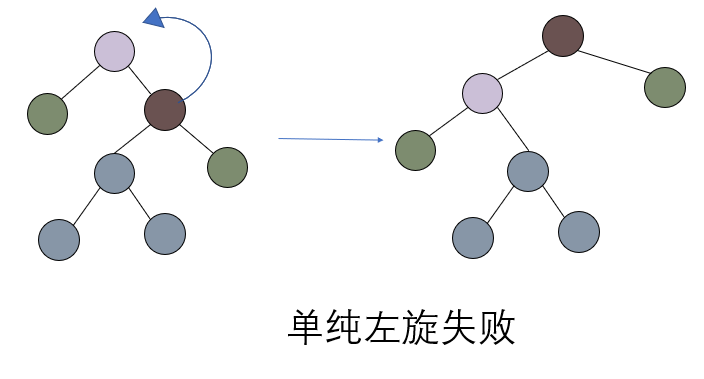
image.png

双旋过来帮个忙

可以看到，左旋后这棵树就变成了左子树高度比右子树高度大于2。究其原因，是因为左旋的时候是需要保证一个被旋转上去的节点其左子树只有一个节点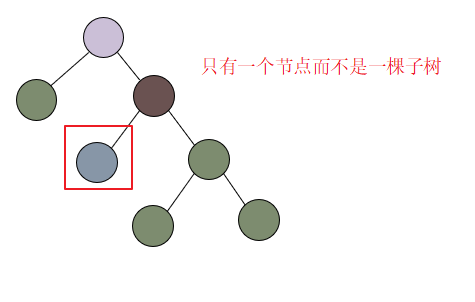
image.png
现在，先通过右旋保证上述的条件；然后再进行左旋。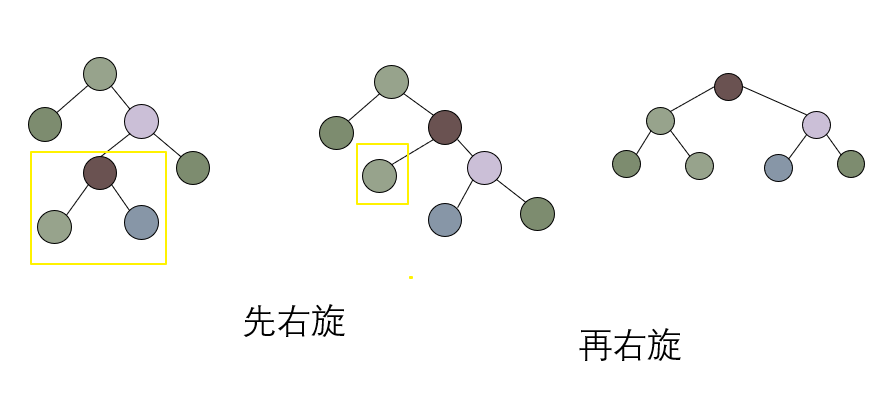
image.png
可以看到，整棵树又已经平衡了。

什么时候用双旋

现在，做一个总结。看一下什么时候使用双旋，什么时候使用单旋。

为了描述方便，引入一个概念叫平衡因子：
AVL树 - 图11

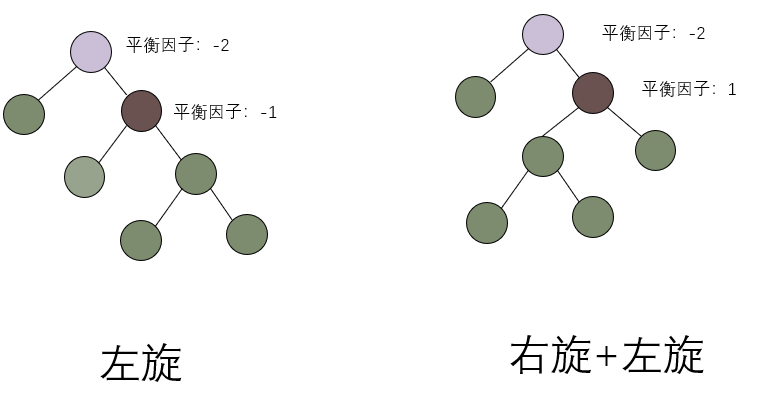
现在，只针对左旋进行一个总结；右旋和左旋本质上是一样的。

  • 如果失衡节点平衡因子为负数，并且其右子树平衡因子为负数，只需要一次左旋；
  • 如果失衡节点平衡因为为负数，并且其右子树平衡因子为正数，需要一次右旋+左旋；

image.png