在学习回溯算法之前，首先得知道递归算法，先来一个最简单的例子

  1. #include <iostream>
  2. #include <vector>
  3. #include <array>
  4. using namespace std;
  6. void backtracking(int x) {
  7.     if (x == 0)
  8.         return;
  9.     backtracking(x - 1);
  10.     cout << x << endl;
  12. }
  14. int main() {
  15.     backtracking(3);
  16.     return 0;
  17. }

上述代码的输出结果为
image.png
可以看到，虽然3是最先进去的，但是却是最晚出来的。

而生活中的一些例子就是这样一个过程，比如对 x = {1, 2, 3, 4}进行组合，我们对它进行组合的规律是；
image.png
可以看到，1虽然是最先进去的，却是最后一个和其他数来交换的。和上面递归部分的思想不能说相似，只能是一摸一样。现在就是利用这种思想，来将这种组合问题来给实现。

循环加递归

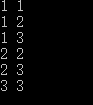
最常用的二层循环如下

  1. for (int i=1; i<4; ++i) {
  2.     for (int j=i; j<4; ++j) {
  3.         cout << i << ' ' << j << endl;
  4.     }
  5. }

image.png
现在不适用二层循环，而是使用循环+迭代，它们之间碰撞出什么样的火花？

  1. #include <iostream>
  2. #include <string>
  3. #include <vector>
  4. using namespace std;
  6. void RecursiveFunction(int x) {
  7.     if (x==4) {
  8.         return ;
  9.     }
  10.     for (int i=x; i<4; ++i) {
  11.         cout << string(x - 1, '\t') << x << i << endl;
  12.         RecursiveFunction(x+1);
  13.         cout << string(x - 1, '\t') << x << i << endl;
  14.     }
  15. }
  18. int main() {
  19.     RecursiveFunction(1);
  20. }

输出如下：
image.png
为什么会产生这样的效果？主要是得益于栈这种结构的优点，而上述的循环+迭代可以被用于一些算法的实现，下面看一下是怎么使用他们的。