1.攻防世界初级区最后一题

已知椭圆曲线加密Ep(a,b)参数为
p = 15424654874903
a = 16546484
b = 4548674875
G(6478678675,5636379357093)
私钥为
k = 546768
求公钥K(x,y)

2.根据圆锥曲线的加密原理，写出解密脚本如下：

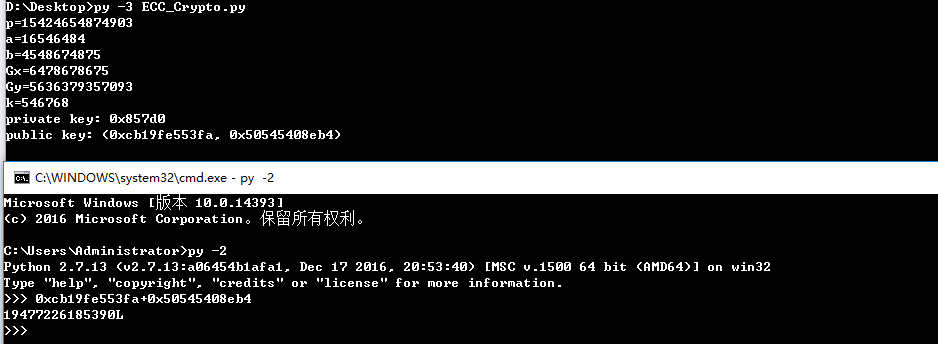
  1. import collections
  2. import random
  4. EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
  6. curve = EllipticCurve(
  7.    'secp256k1',
  8.    # Field characteristic.
  9.    p=int(input('p=')),
  10.    # Curve coefficients.
  11.    a=int(input('a=')),
  12.    b=int(input('b=')),
  13.    # Base point.
  14.    g=(int(input('Gx=')),
  15.       int(input('Gy='))),
  16.    # Subgroup order.
  17.    n=int(input('k=')),
  18.    # Subgroup cofactor.
  19.    h=1,
  20. )
  23. # Modular arithmetic ##########################################################
  25. def inverse_mod(k, p):
  26.    """Returns the inverse of k modulo p.
  28.   This function returns the only integer x such that (x * k) % p == 1.
  30.   k must be non-zero and p must be a prime.
  31.   """
  32.    if k == 0:
  33.        raise ZeroDivisionError('division by zero')
  35.    if k < 0:
  36.        # k ** -1 = p - (-k) ** -1 (mod p)
  37.        return p - inverse_mod(-k, p)
  39.    # Extended Euclidean algorithm.
  40.    s, old_s = 0, 1
  41.    t, old_t = 1, 0
  42.    r, old_r = p, k
  44.    while r != 0:
  45.        quotient = old_r // r
  46.        old_r, r = r, old_r - quotient * r
  47.        old_s, s = s, old_s - quotient * s
  48.        old_t, t = t, old_t - quotient * t
  50.    gcd, x, y = old_r, old_s, old_t
  52.    assert gcd == 1
  53.    assert (k * x) % p == 1
  55.    return x % p
  58. # Functions that work on curve points #########################################
  60. def is_on_curve(point):
  61.    """Returns True if the given point lies on the elliptic curve."""
  62.    if point is None:
  63.        # None represents the point at infinity.
  64.        return True
  66.    x, y = point
  68.    return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0
  71. def point_neg(point):
  72.    """Returns -point."""
  73.    assert is_on_curve(point)
  75.    if point is None:
  76.        # -0 = 0
  77.        return None
  79.    x, y = point
  80.    result = (x, -y % curve.p)
  82.    assert is_on_curve(result)
  84.    return result
  87. def point_add(point1, point2):
  88.    """Returns the result of point1 + point2 according to the group law."""
  89.    assert is_on_curve(point1)
  90.    assert is_on_curve(point2)
  92.    if point1 is None:
  93.        # 0 + point2 = point2
  94.        return point2
  95.    if point2 is None:
  96.        # point1 + 0 = point1
  97.        return point1
  99.    x1, y1 = point1
  100.    x2, y2 = point2
  102.    if x1 == x2 and y1 != y2:
  103.        # point1 + (-point1) = 0
  104.        return None
  106.    if x1 == x2:
  107.        # This is the case point1 == point2.
  108.        m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
  109.    else:
  110.        # This is the case point1 != point2.
  111.        m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)
  113.    x3 = m * m - x1 - x2
  114.    y3 = y1 + m * (x3 - x1)
  115.    result = (x3 % curve.p,
  116.              -y3 % curve.p)
  118.    assert is_on_curve(result)
  120.    return result
  123. def scalar_mult(k, point):
  124.    """Returns k * point computed using the double and point_add algorithm."""
  125.    assert is_on_curve(point)
  129.    if k < 0:
  130.        # k * point = -k * (-point)
  131.        return scalar_mult(-k, point_neg(point))
  133.    result = None
  134.    addend = point
  136.    while k:
  137.        if k & 1:
  138.            # Add.
  139.            result = point_add(result, addend)
  141.        # Double.
  142.        addend = point_add(addend, addend)
  144.        k >>= 1
  146.    assert is_on_curve(result)
  148.    return result
  151. # Keypair generation and ECDHE ################################################
  153. def make_keypair():
  154.    """Generates a random private-public key pair."""
  155.    private_key = curve.n
  156.    public_key = scalar_mult(private_key, curve.g)
  158.    return private_key, public_key
  162. private_key, public_key = make_keypair()
  163. print("private key:", hex(private_key))
  164. print("public key: (0x{:x}, 0x{:x})".format(*public_key))

根据题目提示flag为公钥相加的值，提交的时候把末尾的**L**去掉
image.png