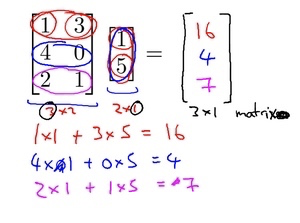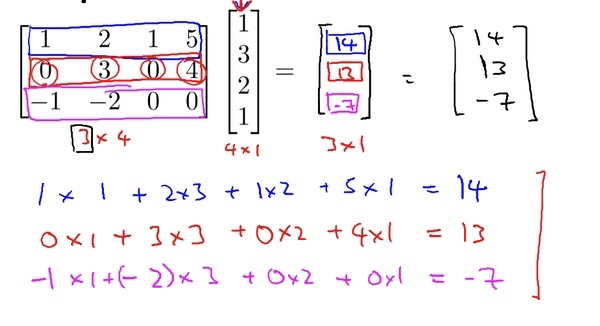第三章 线性代数回顾（Linear Algebra Review）

矩阵

矩阵和向量

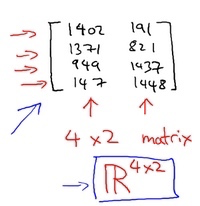
如图，这个是 4×2 矩阵，即4行2列，如 为行， 为列，那么 ，即4×2。

矩阵元素（矩阵项），其中 表示第 行，第 列的元素：
向量（vector）是一种特殊的矩阵，向量一般都是列向量，如：，为四维列向量（）。

加法和标量乘法

矩阵的加法：行列数相等的可以加。例：

矩阵的乘法，每个元素都要乘：

矩阵向量乘法

矩阵和向量的乘法如图：

算法举例：

矩阵乘法

矩阵乘以 矩阵，变成 矩阵。如果这样说不好理解的话就举一个例子来说明一下，比如说现在有两个矩阵 和 ，那么它们的乘积就可以表示为如下的形式。

矩阵乘法的性质

矩阵的乘法不满足交换律：
矩阵的惩罚满足结合律：

单位矩阵（Identity Matrix）：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1,我们称这种矩阵为单位矩阵。它是个方阵，一般用 或者 表示，本讲义都用 代表单位矩阵，从左上角到右下角的对角线（称为主对角线）上的元素均为 ，以外全都为 。如：

对于单位矩阵，有

矩阵逆、转置（Inverse and Transpose）

矩阵的逆：如矩阵 是一个 矩阵（方阵），如果有逆矩阵，则：
矩阵转置：设 为 阶矩阵（即 行 列），第 行 列的元素是 ，即：，定义 的转置为这样一个 阶矩阵 ，满足 ，即 ，记 。直观来看，将 的所有元素绕着一条从第1行第1列元素出发的右下角45度的射线作镜面反转，即得到 的转置。例：

矩阵转置的基本性质：

Matrices that don’t have aninverse are “singular” or “degenerate”，意思说不可逆矩阵又称为奇异矩阵或退化矩阵。

以上就是本章节对线性代数最基本概念的复习。