分类

  • 整型 integers
  • 浮点型
  • 布尔型

    整型

    整型说白了就是平时所见的整数，Python 3的整型已经与长整型进
    行了无缝结合，现在Python 3的整型类似于Java的BigInteger类型，它的
    长度不受限制，如果说非要有个限制，那只限于计算机的虚拟内存总
    数。
    所以，使用Python 3可以很容易地进行大数运算：
    1. >>> 149597870700 / 299792458
    2. 499.00478383615643

    Python可以处理任意大小的整数，当然包括负整数，在程序中的表示方法和数学上的写法一模一样，例如：1，100，-8080，0，等等。 计算机由于使用二进制，所以，有时候用十六进制表示整数比较方便，十六进制用0x前缀和0-9，a-f表示，例如：0xff00，0xa5b4c3d2，等等。 对于很大的数，例如10000000000，很难数清楚0的个数。Python允许在数字中间以_分隔，因此，写成10_000_000_000和10000000000是完全一样的。十六进制数也可以写成0xa1b2_c3d4。

整型的的精度是非常高的，但是整型的除法运算结果为浮点型。
image.png

浮点型

浮点型就是平时所说的小数，例如，圆周率3.14就是一个浮点型数
据，再例如地球到太阳的距离约1.5×108km，也是一个浮点型。Python
区分整型和浮点型的唯一方式，就是看有没有小数点。

浮点数也就是小数，之所以称为浮点数，是因为按照科学记数法表示时，一个浮点数的小数点位置是可变的，比如，1.23x109和12.3x108是完全相等的。浮点数可以用数学写法，如1.23，3.14，-9.01，等等。但是对于很大或很小的浮点数，就必须用科学计数法表示，把10用e替代，1.23x109就是1.23e9，或者12.3e8，0.000012可以写成1.2e-5，等等。

整数和浮点数在计算机内部存储的方式是不同的，整数运算永远是精确的（除法难道也是精确的？是的！），而浮点数运算则可能会有四舍五入的误差。

Python的小数运算是不准确的（是因为和C语言一样采用了IEEE754的标准来存储浮点数的），如下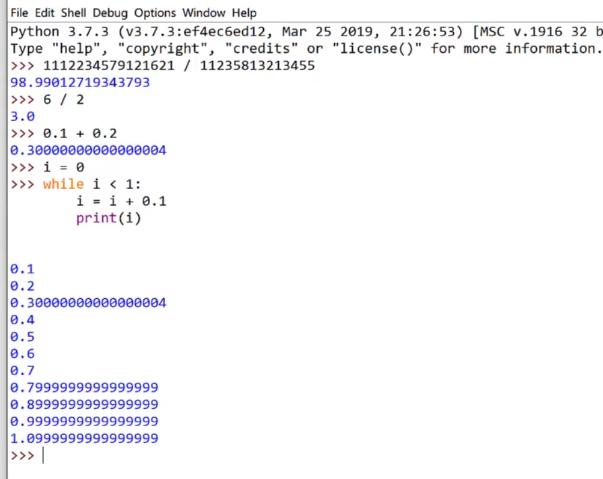
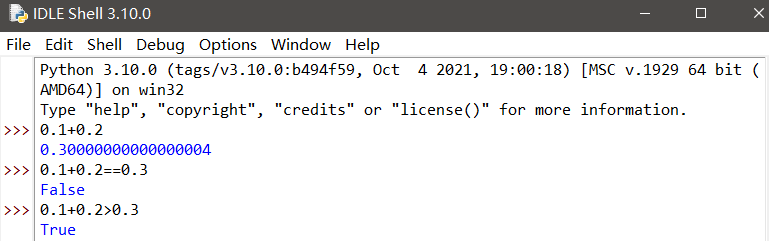
image.png
image.png

如何精确的计算浮点数

引用decimal模块，然后使用decimal的Decimal来实例化一个对象，然后赋值给变量。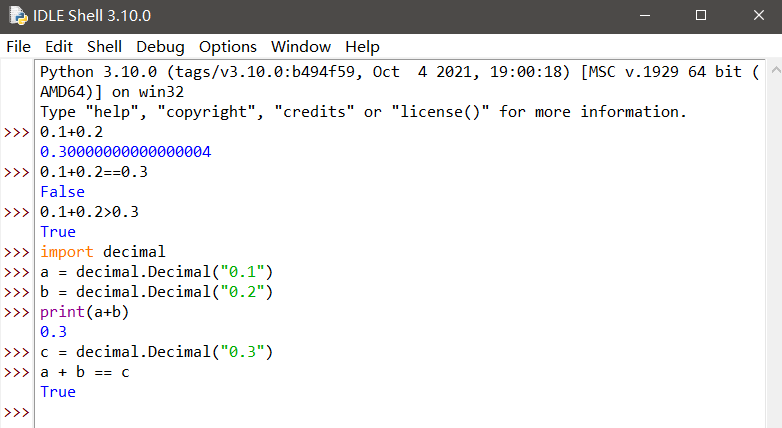
image.png

运算

image.png
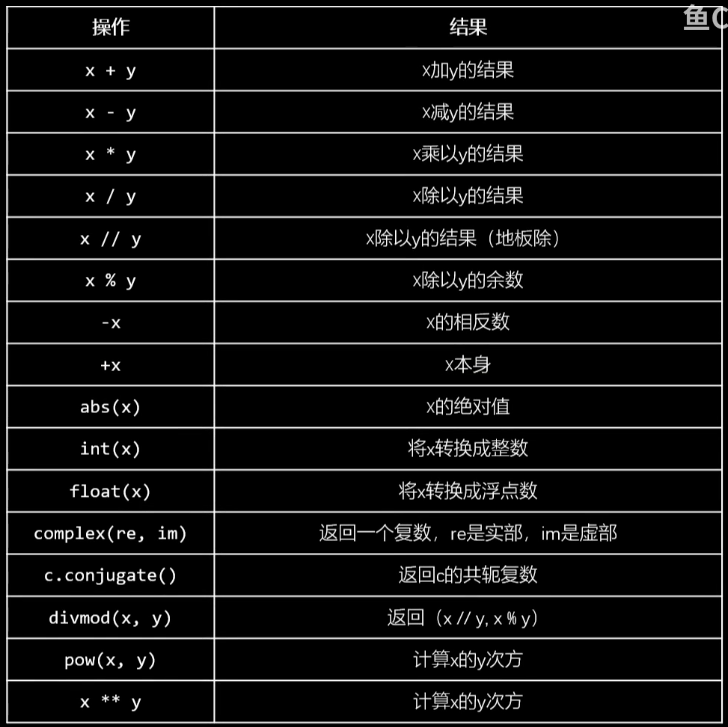
//：向下取整的除法。3//2结果为1，-3//2结果为-2。

%：求两个相除的余数，整除，余数为0，非整除，余数为剩下的数。
**X == (x // y) * y + (x % y)**

divmod(x,y):同时求出除法向下取整的值和除法的余数。

  1. divmod(3,2)
  2. (1, 1)
  3. divmod(6,2)
  4. (3, 0)
  5. divmod(-3,2)
  6. (-2, 1)

abs()：取绝对值。

  1. x = -520
  2. abs(x)
  3. 520
  4. y = -3.14
  5. abs(y)
  6. 3.14

如果abs()参数为复数，那么结果为复数的模

int()：直接截取整数部分取整，同时也可以将整数型的字符串装换为整型数字。不可将小数型的字符串装换。

  1. int(3.14)
  2. 3
  3. int("3.14")
  4. Traceback (most recent call last):
  5.   File "<pyshell#7>", line 1, in <module>
  6.     int("3.14")
  7. ValueError: invalid literal for int() with base 10: '3.14'
  8. int("314")
  9. 314

float：将整型的数字装换为浮点型，同时也可以将小数型的字符串装换为浮点型数字。也可将科学计数型的字符串转换为浮点型数字。

  1. float(520)
  2. 520.0
  3. float("3.14")
  4. 3.14
  5. float("1E6")
  6. 1000000.0

pow(x,y) x ** y:求次方，pow(x,y,z)支持第三个参数，意思是x的y次方然后在除z，求出余数，如下图。

  1. pow(2,4)
  2. 16
  3. 2 ** 4
  4. 16
  6. pow(2,3,3)
  7. 2
  8. 2 ** 3 % 3
  9. 2