1、数据结构分类
- 1.1 逻辑结构（为主）
- 1.2 物理结构（如何去实现逻辑结构）
2、线性表的顺序实现（动态数组）
3、线性表的链式实现（单向链表）
4、栈 (弹夹)
- 4.1 栈的顺序存储
  - 4.1.1 初始化
  - 4.1.2 入栈
- 4.2 栈的链式存储
5、队列
6、散列表
- 6.1 开放寻址法
- 6.2 分离链接法（常用）
7、二叉树
8、图
———————-算法——————————-
10.贪心算法
11.动态规划
12.回溯算法

vs快捷键：
选中多行之后同时按下快捷键shift+alt+i即可进入多行编辑的状态

1、数据结构分类

1.1 逻辑结构（为主）

线性结构：一对一（线性表）
线性表、栈、队列
非线性结构：树形结构：一对多（二叉树）
图形结构：多对多【顶点、有向边（弧）、权值】

1.2 物理结构（如何去实现逻辑结构）

顺序存储
链式存储
不管用哪种物理结构实现，都必须反应出一种逻辑结构

ADT（abstract data type）：抽象数据类型，指一个数学模型以及定义在此数学模型上的一组操作

2、线性表的顺序实现（动态数组）

1、用户使用我们提供的动态数组无法确定类型？
2、用户使用的数据不知道开辟到哪里？
不管用户数据是什么类型，不管用户数据开辟到栈区还是堆区，总之这些数据都会放入到内存中，既然放入到内存中，就会有地址，我们可以用void 接收地址，这里定义void *来维护这个线性空间。

逻辑结构如图：
c语言版数据结构 - 图1

2.0 结构体定义

struct dynamicArray{
    void ** pAddr;        //指向真实维护在堆区数组的指针
    int m_capacity;        //数组的容量
    int m_size;            //数组中元素个数
}

2.1 初始化数组

    struct dynamicArray* array = (struct dynamicArray*)malloc(sizeof(struct dynamicArray));
    //设置容量和大小
    array->m_capacity = capacity;
    array->m_size = 0;
    //设置维护在堆区数组的指针
    array->pAddr = (void**)malloc(sizeof(void**) * array->m_capacity);

2.2 插入元素

插入函数有三个参数（struct dynamicArray array, int pos, void data），array是传入的动态数组，pos是插入的位置，data是需要插入的元素。
先判断插入的位置是否溢出（针对的是size，不是capacity），如果溢出，将其直接插入到尾部。
再判断数组是否满载

    //核心
    if (array->m_size >= array->m_capacity)        //判断数组是否满载
    {
        //1、申请一个更大的新空间
        int NewCapacity = array->m_capacity * 2;
        //2、创建一个新空间
        void** NewSpace = (void**)malloc(sizeof(void*)*NewCapacity);
        //3、将原有数据拷贝到新空间下面
        memcpy(NewSpace, array->pAddr, sizeof(void*)*array->m_capacity);
        //4、释放原有空间
        free(array->pAddr);
        //5、更改指针指向
        array->pAddr = NewSpace;
        //6、更新容量大小
        array->m_capacity = NewCapacity;
    }

在指定位置进行插入

    //从最后一个位置依次后移
    for (int i = array->m_size - 1; i >= pos; i--) {
        array->pAddr[i + 1] = array->pAddr[i];
    }
    //在pos处插入data
    array->pAddr[pos] = data;
    //更新array->m_size
    array->m_size++;

2.3 遍历元素

2.4 删除元素

2.4.1 通过pos来删除

2.4.2 通过data来删除

2.5 销毁数组

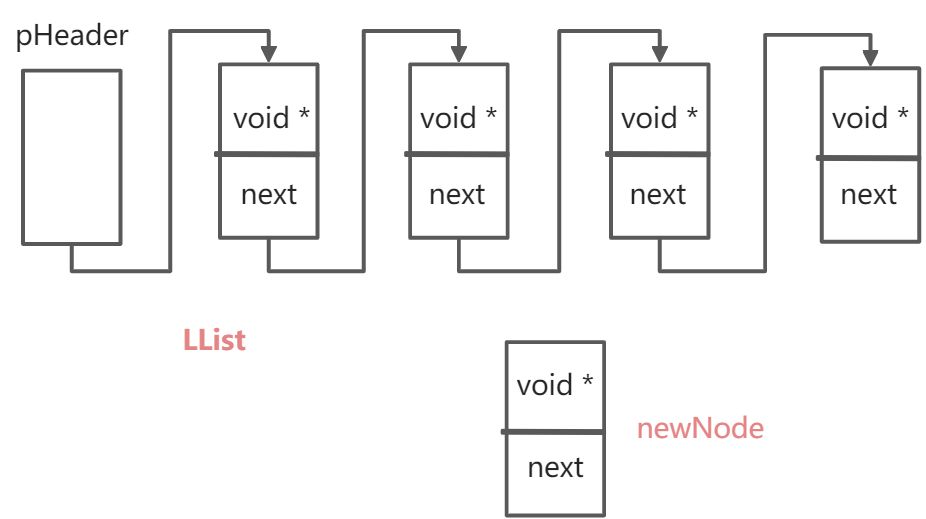
3、线性表的链式实现（单向链表）

c语言版数据结构 - 图2

3.0 结构体定义

这里定义两个结构体：链表的单个结点和链表结构体

//链表单个结点
struct LinkNode        
{
    void * data;                //数据域
    struct LinkNode* next;        //指针域
};

//链表结构体
struct LList                    
{
    struct LinkNode pHeader;    //链表头节点
    int m_size;                    //链表长度
};

//为了不让用户拿到链表中具体的属性进行误操作，给用户提供另一个接口，返回void*
typedef void* LinkList;
//在需要访问时，将void* 还原回去LList
LinkList list=NULL;
struct LList* myList = list;

3.1 初始化链表

创建链表，然后置为空。

//初始化链表
//如果要拿到链表的size，先将LinkList(void*)还原回LList*   ,这里void*和struct LList*无缝衔接！
LinkList init_LinkList()
{
    //虽然开辟的是LList*，但返回的是LinkList（void*）,用户拿到的是void*,不能操作具体的属性
    struct LList* myList = (struct LList*)malloc(sizeof(struct LList));
    if (NULL == myList)
    {
        return NULL;
    }
    //置为空
    myList->pHeader.data = NULL;
    myList->pHeader.next = NULL;
    myList->m_size = 0;
    return myList;
}

3.2 插入结点

先创建临时结点指向链表头，通过循环找到插入位置的前驱结点
创建需要插入的新结点 struct LinkNode* newNode

void insert_LinkList(LinkList list, int pos, void* data)
{
    //将LinkList还原回去LList
    struct LList* myList = list;
    //无效位置进行尾插
    if (pos<0 || pos>myList->m_size)
    {
        pos = myList->m_size;
    }
    //创建临时结点
    struct LinkNode* pCurrent = &myList->pHeader;
    //通过循环找到插入位置的前驱结点
    for (int i = 0; i < pos; i++)
    {
        pCurrent = pCurrent->next;
    }
    //创建需要插入的新结点
    struct LinkNode* newNode = (struct LinkNode*)malloc(sizeof(struct LinkNode));
    newNode->data = data;
    newNode->next = NULL;
    //插入
    newNode->next = pCurrent->next;
    pCurrent->next = newNode;
    //更新链表长度
    myList->m_size++;
}

3.3 遍历链表

定义临时变量指向第一个有数据的结点，然后往后遍历。

//伪代码    
    //将临时变量指向第一个有数据的结点
    struct LinkNode* pCurrent = myList->pHeader.next;
    for (int i = 0; i < myList->m_size; i++)
    {
        myPrint(pCurrent->data);

        pCurrent = pCurrent->next; //核心，往后移
    }

3.4 删除结点

3.4.1 按位置删除

通过循环找到插入位置的前驱结点，然后将该位置做标记，改变指针指向后释放改位置。

//伪代码    
    //创建临时结点
    struct LinkNode* pCurrent = &myList->pHeader;
    //通过循环找到插入位置的前驱结点
    for (int i = 0; i < pos; i++)
    {
        pCurrent = pCurrent->next;
    }
    //标记将待删除的结点，方便后面释放
    struct LinkNode* pDele = pCurrent->next;
    pCurrent->next = pDele->next;
    free(pDele);
    pDele = NULL;

    //更新链表长度
    myList->m_size--;

3.4.2 按数据删除

定义两个辅助结点指针变量pPrev和pCurrent，同时遍历，当遍历到被删数据时，第一个指针变量的next指向被删数据指针的next。

//伪代码    
    struct LinkNode* pPrev = &myList->pHeader;
    struct LinkNode* pCurrent = pPrev->next;
    for (int i = 0; i < myList->m_size; i++)
    {
        //回调函数3  myCompare(void*, void*)交给用户进行比较
        if (myCompare(pCurrent->data, data))        
        {
            pPrev->next = pCurrent->next;
            free(pCurrent);
            pCurrent = NULL;
            //更新链表长度
            myList->m_size--;
            break;
        }
        //将辅助指针后移
        //pCurrent++;
        //pPrev++;
        pPrev = pCurrent;
        pCurrent = pCurrent->next;
    }

3.5清空链表

定义变量pCurrent指向第一个有数据的结点，然后往后遍历，记得再定义一个后继结点记住pCurrent的下一个位置，不然删除之后链表就断了。

void clear_LinkList(LinkList list)
{
    //从第一个有数据的结点开始,从前往后清空
    struct LinkNode* pCurrent = myList->pHeader.next;    //第一次写错了&myList->pHeader
    for (int i = 0; i < myList->m_size; i++)
    {
        //标记将删除结点的后继结点
        struct LinkNode* pNext = pCurrent->next;
        free(pCurrent);
        pCurrent = pNext;

    }
    //头结点的指针指向空
    myList->pHeader.next = NULL;
    myList->m_size = 0;
}

3.6销毁链表

void destroy_LinkList(LinkList list)
{
    free(list);
    list = NULL;
}

4、栈 (弹夹)

栈不可以遍历，只有栈顶元素可以被外界访问
什么叫遍历：不重复不遗漏访问容器中的所有数据，遍历算法属于非质变算法，如果你想遍历栈，那你就会进行出栈操作，使栈中的数据发生变化，这是不允许的。
应用：逆序操作、数值转换、括号匹配、迷宫求解
括号匹配设计思想：（就近原则）
从第一个字符开始扫描当遇见普通字符时忽略，当遇见左括号时压入栈中，当遇见右括号时从栈中弹出栈顶符号，并进行匹配
1、匹配成功，最终扫描完毕且栈为空
2、循环遍历，发现栈为空，但多余的右括号匹配失败：立即停止，并报错结束
3、所有字符扫描完毕但栈非空，左括号多余

4.1 栈的顺序存储

设计时：栈顶放在数组的尾地址（效率高）
通过top指针的变化来实现增减数据，对于出栈操作不需要释放啥，等下次新进来的元素会自动覆盖掉原来的数据。

4.1.1 初始化

4.1.2 入栈

判断是否栈满，如果满了就不能继续入栈。对于没有存满的栈，直接在栈顶继续插入

    myStack->data[myStack->m_size] = data;
    myStack->m_size++;

4.2 栈的链式存储

设计时：栈顶放在链表的头地址（效率高），放在尾部的话每次插入删除都需要从头遍历

5、队列

循环队列
双端队列
优先队列

6、散列表

散列表也叫作哈希表（hash table），这种数据结构提供了键（Key）和值（Value）的映射关系。只要给出一个Key，就可以高效查找到它所匹配的Value，时间复杂度接近于O(1) 。
应用：在线拼写检测功能

散列表的Key多是以字符串类型为主。因此需要一个“中转站”，通过某种方式，把Key和数组下标进行转换。这个中转站就是哈希函数，我们可以把字符串或其他类型的Key，转化成数组的下标index，然后进行遍历，但有可能出现不同的 Key通过哈希函数获得的下标有可能是相同的，这就是哈希冲突。解决哈希冲突的方法主要有两种，一种是开放寻址法(线性探测)，一种是分离链接法。

6.1 开放寻址法

开放寻址法的原理很简单，当一个Key通过哈希函数获得对应的数组下标已被占用时，我们可以“另谋高就”，寻找下一个空档位置（固定长度）。这就是线性探测，当然如果下面很大一块区域都是被占用的，觉得一次寻址一个固定长度太慢就用平方探测，随着次数的增加寻址的长度也就更长。

6.2 分离链接法（常用）

 对于不同的 Key值通过哈希函数获得的下标有可能是相同的哈希冲突问题，可以对下标的元素添加“小尾巴”来解决，这个小尾巴就是以链表的形式链接在重复元素的后面。<br /> **所以散列表可以说是数组和链表的结合**<br />下面以C语言实现散列表:[C语言](http://www.martinbroadhurst.com/hash-table.html)

#ifndef HASHTABLE_H
#define HASHTABLE_H

struct hashnode {
    void * data;
    struct hashnode * next;
};

typedef struct hashnode hashnode;    //自定义类型名

typedef int (*hashtable_cmpfn)(const void*, const void*);
typedef unsigned long (*hashtable_hashfn)(const void*);
typedef void (*hashtable_forfn)(void *);
typedef void (*hashtable_forfn2)(void *, void *);

struct hashtable {
    unsigned int size;
    hashtable_hashfn hash;
    hashtable_cmpfn compare;
    hashnode **buckets;            //“指针的指针”，buckets是hashnode数组（篮子）
    size_t count;
};

typedef struct hashtable hashtable;

hashtable *hashtable_create(size_t size, hashtable_cmpfn compare);
void hashtable_empty(hashtable * table);
void hashtable_delete(hashtable * table);
void *hashtable_add(hashtable * table, void * data);
void *hashtable_find(const hashtable * table, const void * data);
void *hashtable_remove(hashtable * table, const void * data);
float hashtable_get_load_factor(const hashtable * table);
unsigned int hashtable_get_count(const hashtable * table);
unsigned int hashtable_find_count(const hashtable *table);
void hashtable_for_each(const hashtable * table, hashtable_forfn fun);
void hashtable_for_each2(const hashtable * table, hashtable_forfn2 fun, void *data);
void hashtable_set_hashfn(hashtable * table, hashtable_hashfn hash);

#endif /* HASHTABLE_H */

#include <stdlib.h>
#include <hashtable.h>

hashnode * hashnode_create(void * data)
{
    hashnode * node = malloc(sizeof(hashnode));
    if (node) {
        node->data = data;
        node->next = NULL;
    }
    return node;
}

void hashnode_delete(hashnode * node)
{
    free(node);
}

static unsigned long sdbm(const char *str)
{
    unsigned long hash = 0;
    int c;

    while ((c = *str++))
        hash = c + (hash << 6) + (hash << 16) - hash;

    return hash;
}

hashtable * hashtable_create(size_t size, hashtable_cmpfn compare)
{
    hashtable * table = malloc(sizeof (hashtable));
    if (table) {
        table->size = size;
        table->hash = (hashtable_hashfn)sdbm;
        table->compare = compare;
        table->count = 0;
        table->buckets = malloc(size * sizeof(hashnode *));
        if (table->buckets) {
            unsigned int b;
            for (b = 0; b < size; b++) {
                table->buckets[b] = NULL;
            }
        }
        else {
            free(table);
            table = NULL;
        }
    }
    return table;
}

void hashtable_empty(hashtable * table)
{
    unsigned int i;
    hashnode * temp;
    for (i = 0; i < table->size; i++) {
        hashnode * current = table->buckets[i];
        while (current != NULL) {
            temp = current->next;
            hashnode_delete(current);
            current = temp;
        }
        table->buckets[i] = NULL;
    }
    table->count = 0;
}

void hashtable_delete(hashtable * table)
{
    if (table) {
        hashtable_empty(table);
        free(table->buckets);
        free(table);
    }
}

void * hashtable_add(hashtable * table, void * data)
{
    const unsigned int bucket = table->hash(data) % table->size;
    void * found = NULL;

    if (table->buckets[bucket] == NULL) {
        /* An empty bucket */
        table->buckets[bucket] = hashnode_create(data);
    }
    else {
        unsigned int added = 0;
        hashnode * current, * previous = NULL;
        for (current = table->buckets[bucket]; current != NULL && !found && !added; current = current->next) {
            const int result = table->compare(current->data, data);
            if (result == 0) {
                /* Changing an existing entry */
                found = current->data;
                current->data = data;
            }
            else if (result > 0) {
                /* Add before current */
                hashnode * node = hashnode_create(data);
                node->next = current;
                if (previous == NULL) {
                    /* Adding at the front */
                    table->buckets[bucket] = node;
                }
                else {
                    previous->next = node;
                }
                added = 1;
            }
            previous = current;
        }
        if (!found && !added && current == NULL) {
            /* Adding at the end */
            previous->next = hashnode_create(data);
        }
    }
    if (found == NULL) {
        table->count++;
    }

    return found;
}

void * hashtable_find(const hashtable * table, const void * data)
{
    hashnode * current;
    const unsigned int bucket = table->hash(data) % table->size;
    void * found = NULL;
    unsigned int passed = 0;
    for (current = table->buckets[bucket]; current != NULL && !found && !passed; current = current->next) {
        const int result = table->compare(current->data, data);
        if (result == 0) {
            found = current->data;
        }
        else if (result > 0) {
            passed = 1;
        }
    }
    return found;
}

void * hashtable_remove(hashtable * table, const void * data)
{
    hashnode * current, * previous = NULL;
    const unsigned int bucket = table->hash(data) % table->size;
    void * found = NULL;
    unsigned int passed = 0;

    current = table->buckets[bucket];
    while (current != NULL && !found && !passed) {
        const int result = table->compare(current->data, data);
        if (result == 0) {
            found = current->data;
            if (previous == NULL) {
                /* Removing the first entry */
                table->buckets[bucket] = current->next;
            }
            else {
                previous->next = current->next;
            }
            hashnode_delete(current);
            table->count--;
        }
        else if (result > 0) {
            passed = 1;
        }
        else {
            previous = current;
            current = current->next;
        }
    }
    return found;
}


float hashtable_get_load_factor(const hashtable * table)
{
    unsigned int touched = 0;
    float loadfactor;
    unsigned int b;
    for (b = 0; b < table->size; b++) {
        if (table->buckets[b] != NULL) {
            touched++;
        }
    }
    loadfactor = (float)touched / (float)table->size;
    return loadfactor;
}

unsigned int hashtable_get_count(const hashtable * table)
{
    return table->count;
}

unsigned int hashtable_find_count(const hashtable *table)
{
    unsigned int b;
    const hashnode *node;
    unsigned int count = 0;
    for (b = 0; b < table->size; b++) {
        for (node = table->buckets[b]; node != NULL; node = node->next) {
            count++;
        }
    }
    return count;
}

void hashtable_for_each(const hashtable * table, hashtable_forfn fun)
{
    unsigned int b;

    for (b = 0; b < table->size; b++) {
        const hashnode *node;
        for (node = table->buckets[b]; node != NULL; node = node->next) {
            fun(node->data);
        }
    }
}


void hashtable_for_each2(const hashtable * table, hashtable_forfn2 fun, void *data)
{
    unsigned int b;

    for (b = 0; b < table->size; b++) {
        const hashnode *node;
        for (node = table->buckets[b]; node != NULL; node = node->next) {
            fun(node->data, data);
        }
    }
}

void hashtable_set_hashfn(hashtable * table, hashtable_hashfn hash)
{
    table->hash = hash;
}

C++:b站视频

7、二叉树

 使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。<br />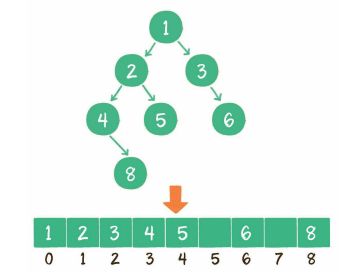![image.png](https://cdn.nlark.com/yuque/0/2021/png/21573913/1639966130533-469887f8-ecf4-467c-8aec-b76273d309a0.png#clientId=u5ddec715-dd7d-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=313&id=ude0917b6&margin=%5Bobject%20Object%5D&name=image.png&originHeight=273&originWidth=350&originalType=binary&ratio=1&rotation=0&showTitle=false&size=38911&status=done&style=none&taskId=ua8e4a9f6-38ef-4707-a284-97c25fcaff4&title=&width=401)<br /> 为什么这样设计呢？因为这样可以更方便地在数组中定位二叉树的孩子 节点和父节点。 假设一个父节点的下标是parent，那么它的左孩子节点下标就 是2×parent + 1 ；右孩子节点下标就是2×parent + 2 。

7.1 深度优先遍历

前序遍历、中序遍历、后续遍历

7.1.1 递归实现

7.1.2 栈实现

7.2 广度优先遍历

层序遍历

7.3 二叉堆

二叉堆本质上是一种完全二叉树，它分为两个类型：大顶堆和小顶堆。二叉堆虽然是一个完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。
对于二叉堆，有如下几种操作。

插入节点。
删除节点。
构建二叉堆。

这几种操作都基于堆的自我调整。所谓堆的自我调整，就是把一个不符合堆性质的完全二叉树，调整成一个堆。

下面以小顶堆为例：

7.3.1 插入

小顶堆中插入新节点一般是上浮操作，

7.3.2 删除

删除堆顶节点一般是下沉操作

7.3.3 构建

对于一个无序完全二叉树，本质就是让所有非叶子节点依次“下沉”，最终每一节点都小于它的左、右孩子节点。

  堆的插入操作是单一节点的“上浮”，堆的删除操作是单一节点的“下沉”，这两个操作的平均交换次数都是堆高度的一半，所以时间复杂度是**O(logn)**。至于堆的构建，需要所有非叶子节点依次“下沉”，所以一般会觉得时间复杂度应该是O(nlogn) ，但构建堆的时间复杂度却并不是 O(nlogn)，而是**O(n)**。

8、图

———————-算法——————————-

解析解（直接套公式）：现实情况根本不可能
近似解（迭代法）：求最优解

10.贪心算法

把整体最优分解为各个阶段的最优选择问题，且不能反悔，最终得到最优解。
速度快、但不能保证每次都是最优解

11.动态规划

将待求解问题分解为若干子问题进行求解，经分解的子问题往往不是相互独立的，对于每次已解决的子问题答案进行保存，这样可以避免重复计算，可以反悔

12.回溯算法

试探法，选择一种可能向前探索，如果不行就退一步回溯，重新选择继续试探，直至找到最优解
对于新增的不可行位置压栈（1），回溯时出栈