超级屏保：3D图形互动 3D星空互动动态卡片效果 - 技能学习：鼠标控制3D图形互动 - 《python知识库》

本期教程带大家做可以用鼠标控制3D图形视角移动的功能。
屏幕录制2022-04-30 23.18.39.2022-04-30 23_29_40.gif

教学过程：

3D投射原理+计算公式
代码实现投射
鼠标键盘事件
物体移动

教学目标：

3D投射原理+计算公式
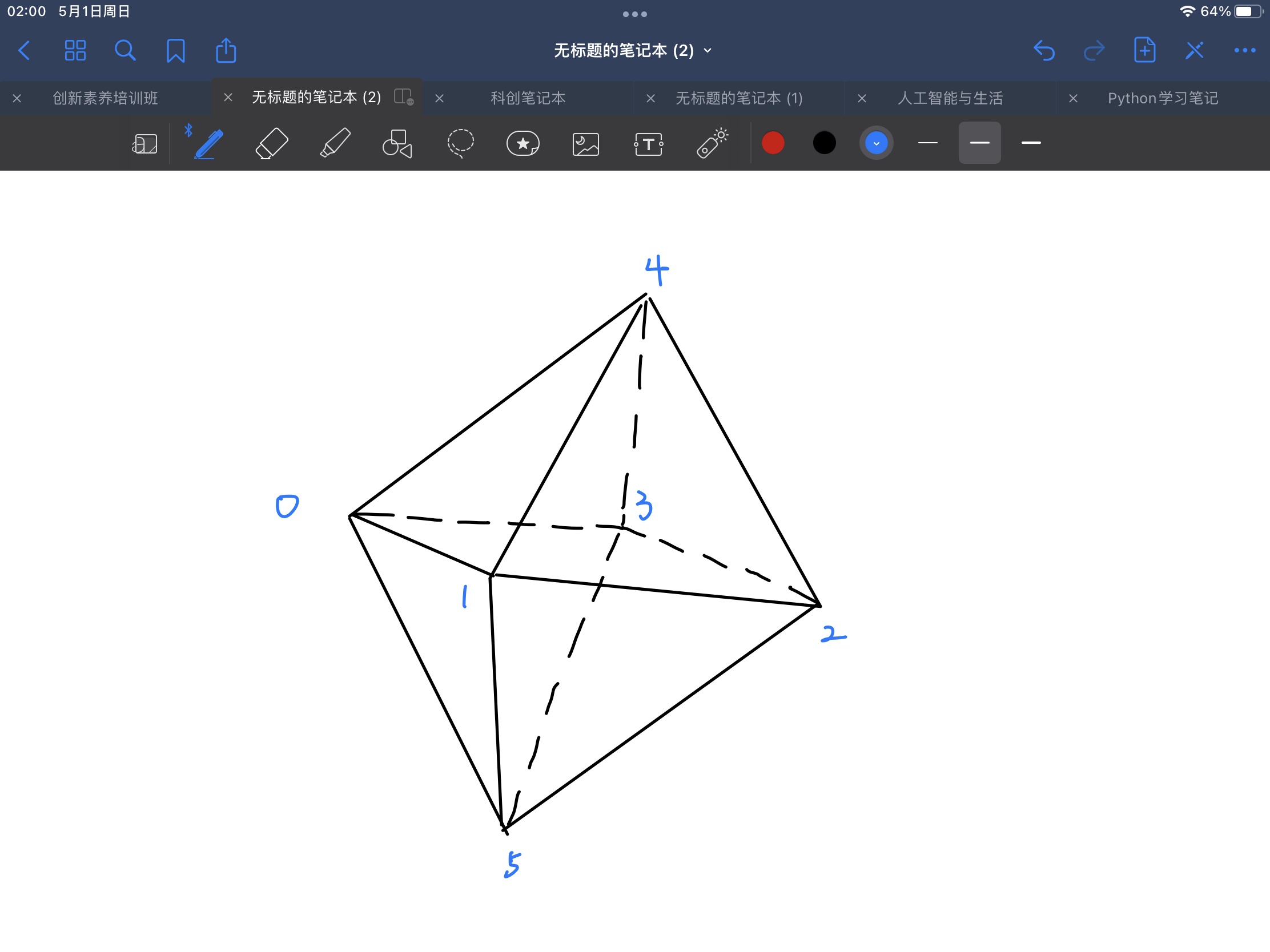
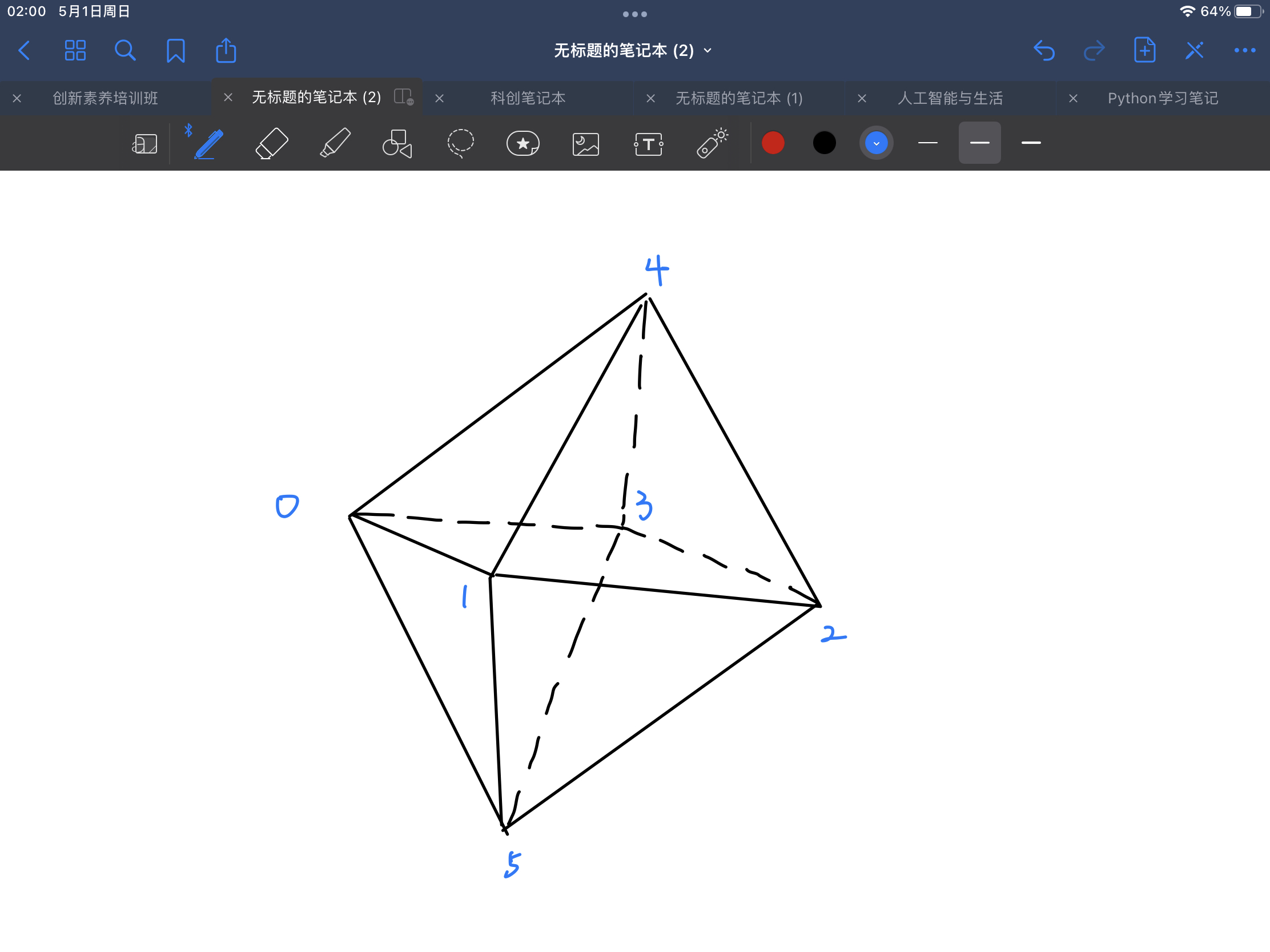
首先需要利用空间坐标系的概念，我们创建一个空间坐标系，定义z轴为xy平面坐标系在纵深方向的扩展。如果我们知道一个立体图形每个点在空间坐标系的坐标，就可以把它在空间坐标系中画出来，比如一个八面体，按照图中标号0-5-1-4-2-5-3-4-0-1-2-3-0这个顺序就可以将八面体画出来。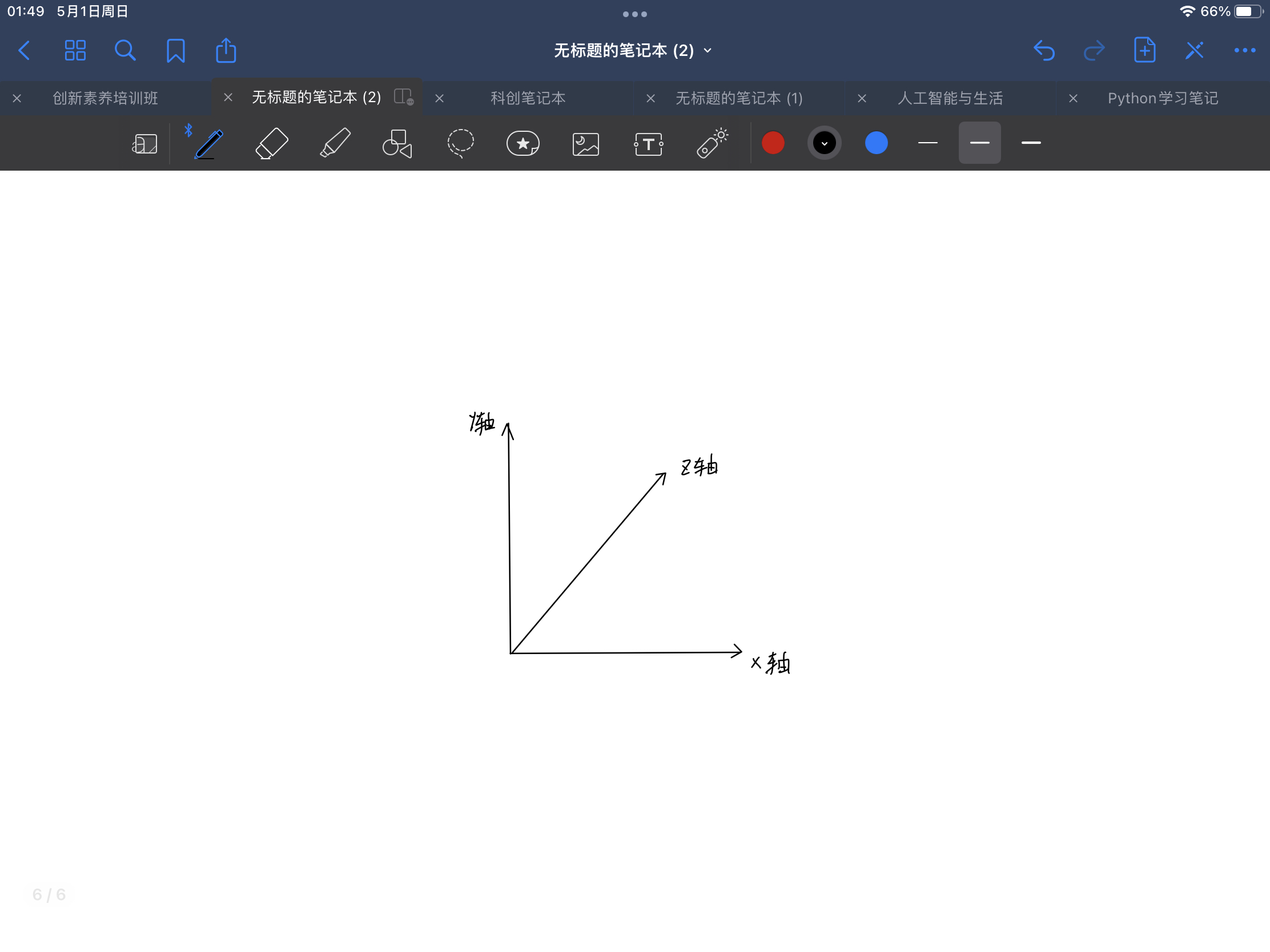

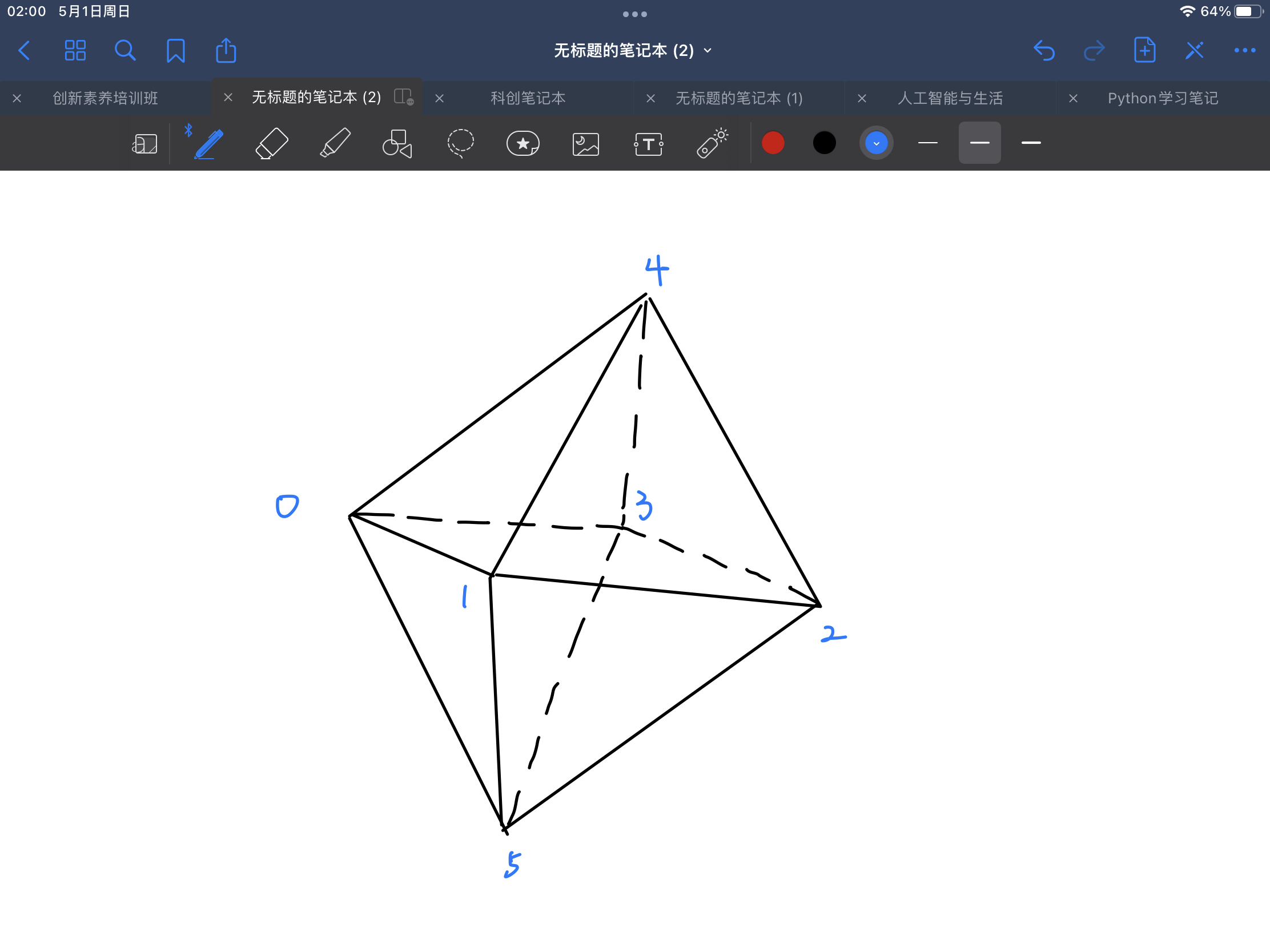
如果我们利用大脑想象一个空间坐标系，很容易就能构思出一个立体图形，想象一下这个八面体，接下来我们再抽象地制定一个对称八面体，以八面体几何中心为坐标点，在空间坐标系中具体的坐标数据。
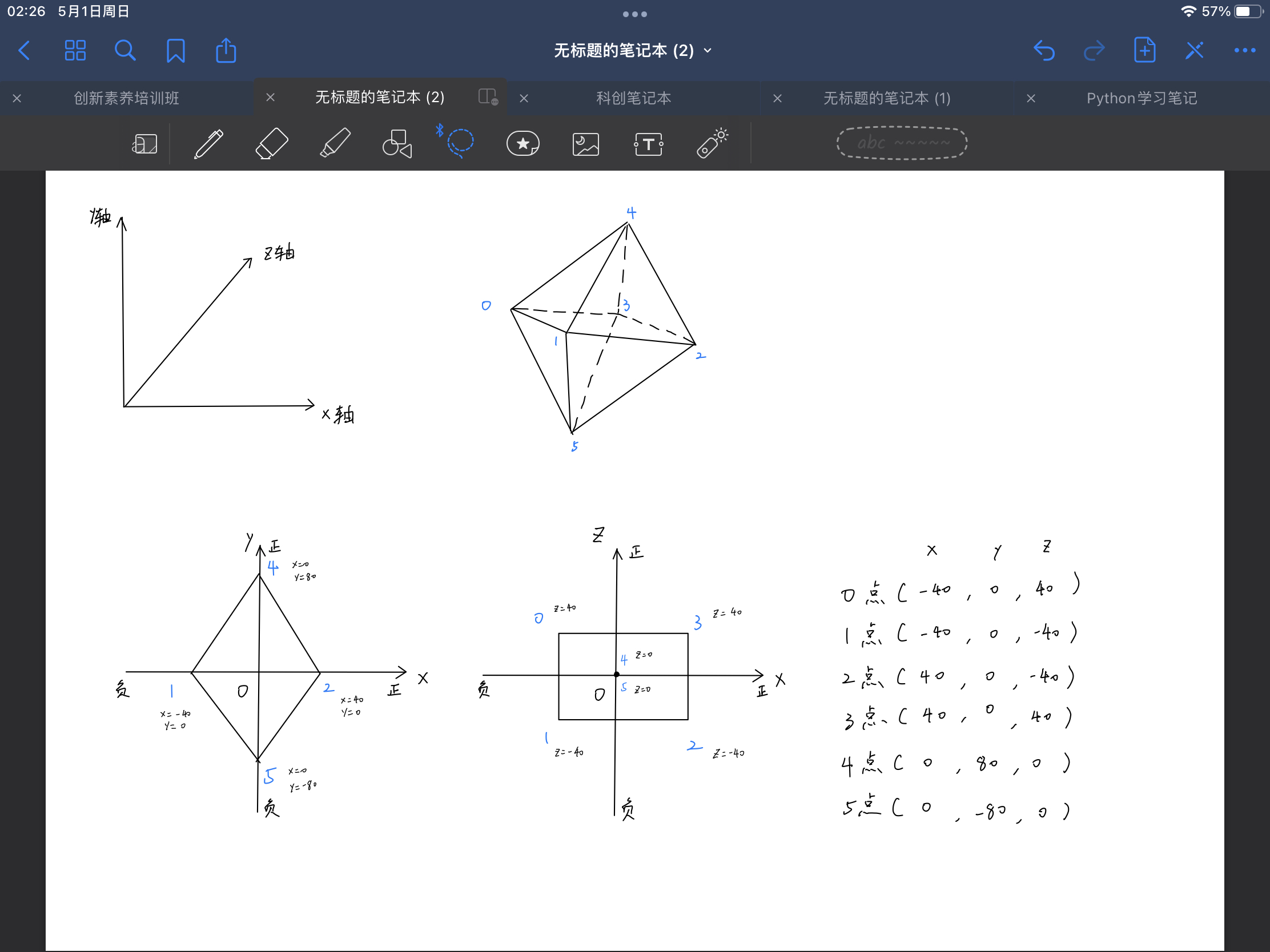
我们先把八面体放到xy坐标系看，相当于从正面看这个八面体。为了便于计算，将12点相对于y轴对称，45点相对于x轴对称，指定12点距离为80，指定45点距离为160，这样就可以得到1、2、4、5点的xy轴坐标值。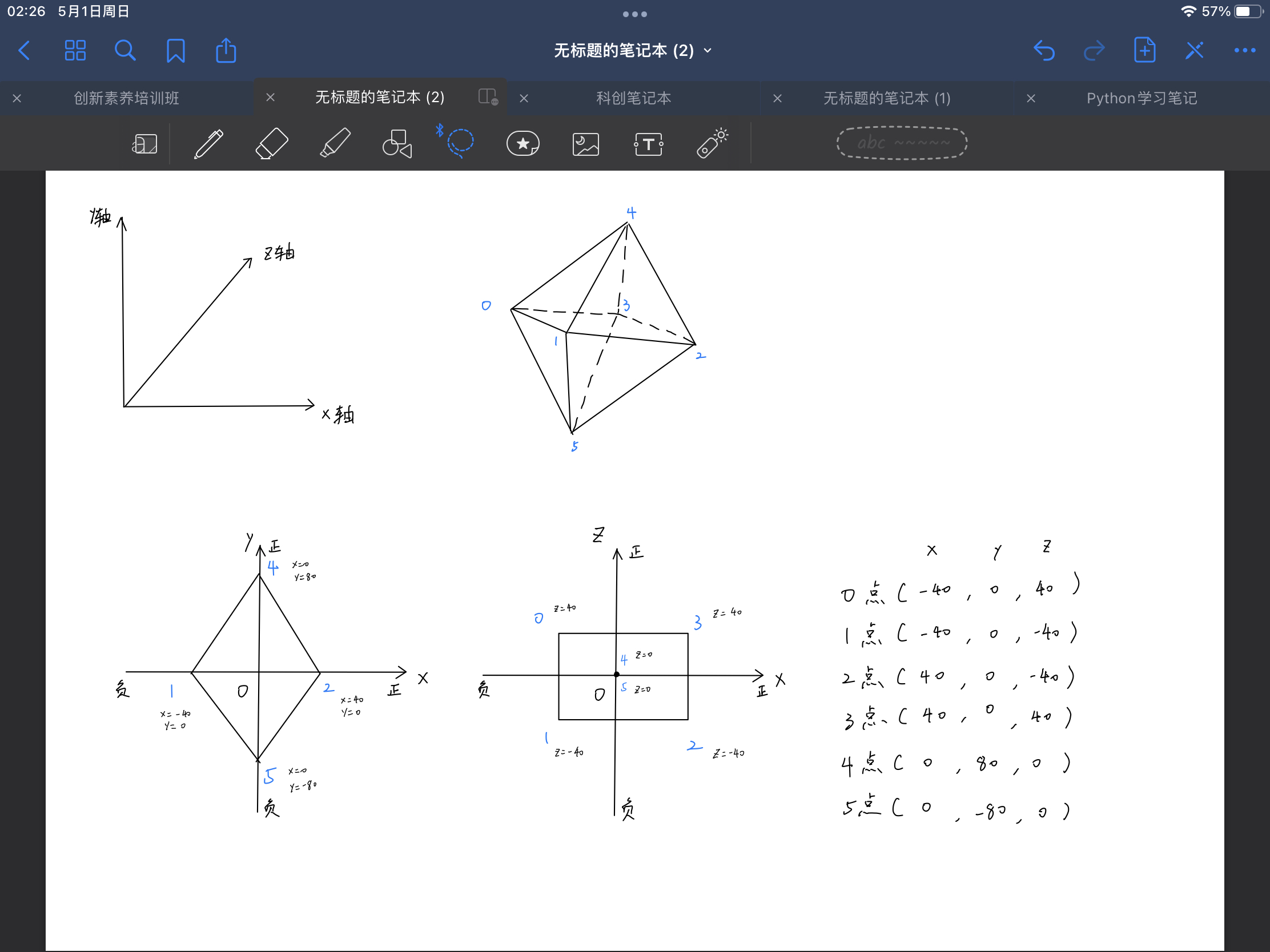

我们再把八面体放到xz坐标系看，相当于从上往下看这个八面体。将03点、12点相对于z轴对称，01点、32点相对于x轴对称，45点则在xz坐标系的坐标原点上（由于八面体的几何中心为空间坐标系原点，将45顶点放在坐标原点的上面和下面），指定13点距离为80，01点距离为80，这样就可以得到0、1、2、3、4、5的z轴坐标值。

最后，经过整理我们得到这个八面体在空间坐标系中的六个顶点坐标，大部分数据是我们直接指定的，只要数据导致最后图形对称，就不影响后续计算，可以自己调整数值以适合显示效果。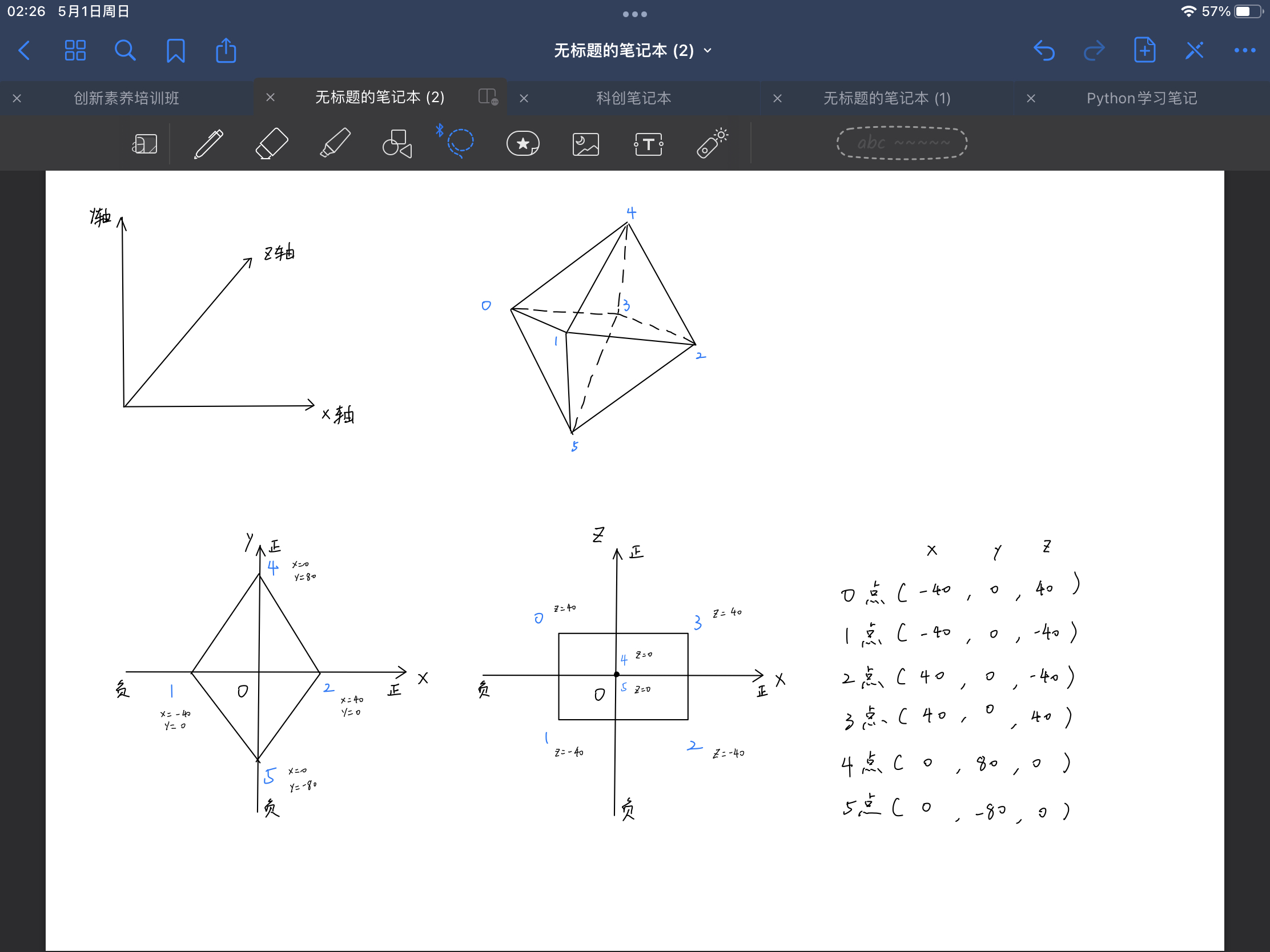

有了这个八面体的坐标点，只要在代码中按照0-5-1-4-2-5-3-4-0-1-2-3-0的顺序不停的绘画，就可以将这个图形显示出来，但最关键的问题是：如何将z轴在画面中表达出来？
在现实世界中看物体是有纵深效果的，一个物体距离人眼睛的距离将决定眼睛看到他的大小：近大远小，如果想要在画面中模仿人眼看到的3D物体移动甚至旋转，要考虑到视角到物体的距离，才能表达出三维世界的美感。可以参照一下四幅不同视角的正方体，在从二维到三维的视觉变化过程。
无标题的笔记本 (2)-7.jpg 截屏2022-05-01 02.49.05.png 截屏2022-05-01 02.49.38.png 截屏2022-05-01 02.49.46.png

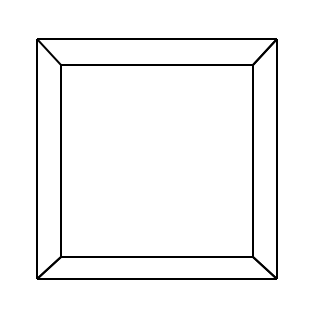
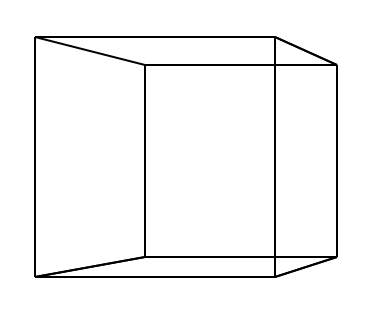
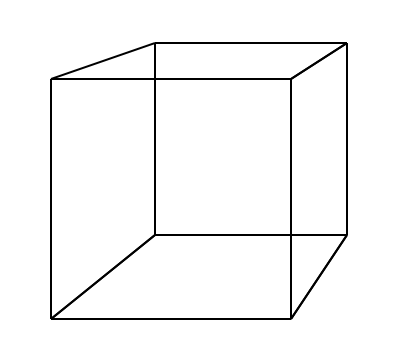
在了解了三维世界的纵深效果之后，我们来学习如何在代码中利用数学公式将z轴纵深效果表达出来。
透视原理：通过对三维世界的观察，将三维物体在二维的平面上进行表现。屏幕上的画面是2D的，我们通过屏幕看到的3D物体，实际上是它根据透视原理在屏幕上的一个2D投射，并且z轴越大，图案的大小越小，即:近大远小。一个3D物体的大小和形状,与:物体位置、摄像机位置、屏幕位置有关。那么在3D内的某点在2D中坐标该如何计算?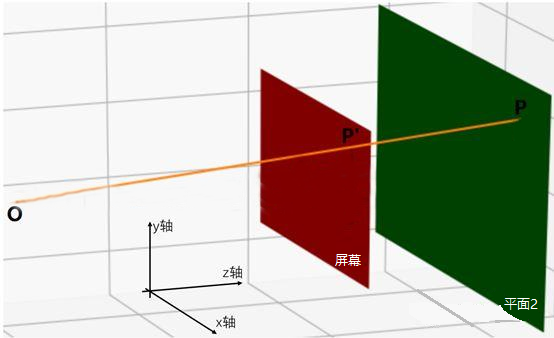

在画面中我们将2D转换成3D世界，由此就有了摄像机视点O、屏幕（红色）、物体所在平面（绿色），定义：红色平面、绿色平面与xy轴平面平行，与z轴垂直。
P点代表3D空间中实际物体的一点，坐标为（x，y，z），O为摄像机位置，要求P在屏幕上投射点P’的位置，该如何求？
P（x,y,z），P’（px,py,pz），O（ox,oy,oz）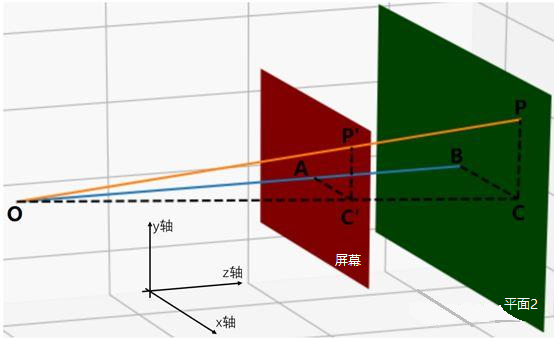

作OB辅助线垂直于绿色平面，在红色平面经过点A，得到：线段OAB与z轴平行；
作PC辅助线垂直于x轴，连接OC，在红色平面经过点C‘，得到：P’C’和PC垂直于x轴；
连接BC、AC’，得到：BC//AC’//绿色平面//红色平面//xy轴平面。
由此我们可以得到，相似三角形OAC’和OBC，得出：
OA/OB=AC’/BC=P’C’/PC（相似三角形特征）
设：
P点坐标（x,y,z）
O点坐标（ox,oy,oz）
OA=pz-oz（OA点之间距离）
OB=z-oz
BC=x-ox
PC=y-oy
AC’=px-ox
求：P’点坐标（px,py,pz）
AC’相当与PO点的x轴距离，AC’=px-ox=OA/OBBC
则：**px=ox+[(pz–oz)/(z-oz)(x-ox)]
P’C’相当于PO点的y轴距离，P’C’=py-oy=OA/OB*PC
则：py=oy+[(pz-oz)/(z-oz)(y-oy)]*
此时我们已经知道P’的xy坐标了，那么z坐标怎么办？不需要去计算，可以直接指定，投射后的z坐标只会影响到物体投射出来的大小，可以根据显示情况自行制定。
接下来，我们需要在python的2D画面中把3D八面体投射画出来，在画之前我们先要在自己心中有一个3D坐标，python的2D画面就是下图中的红色屏幕，假象这个红色屏幕的前方有摄像机视点，后方是实际八面体。我们利用代码将这个八面体的每个点连接起来，按照顺序绘画出来，就能得到实际八面体投射出来的画面了。

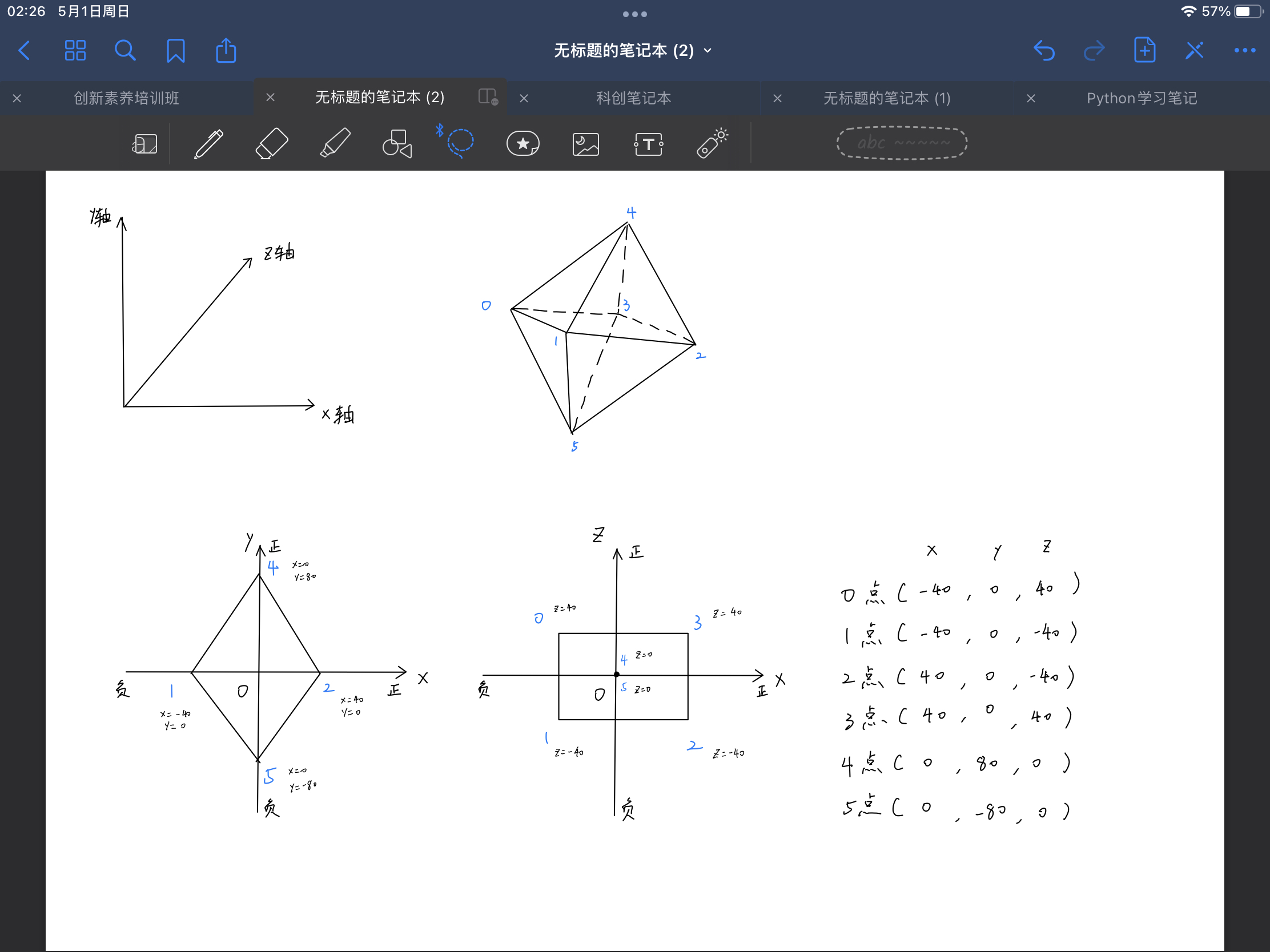
首先我们导入六个点的坐标数据到不同的三个列表内，建立一个自定义函数方便导入，
三个列表分别是：
xList（存放六个点的x轴坐标）
yList（存放六个点的y轴坐标）
zList（存放六个点的z轴坐标）
然后运行六次该自定义函数，将八面体六个点依次导入三个列表中。

xList = []
yList = []
zList = []
def add_coord_init(x, y, z):
    xList.append(x)
    yList.append(y)
    zList.append(z)
add_coord_init(-40, 0, 40) #0点
add_coord_init(-40, 0, -40) #1点
add_coord_init(40, 0, -40) #2点
add_coord_init(40, 0, 40) #3点
add_coord_init(0, 80, 0) #4点
add_coord_init(0, -80, 0) #5点

由于后续需要用到tkinter界面设计中的canvas的create_line内置函数来画八面体，我们先创建一个tkinter界面和canvas画布。

import tkinter as tk
window = tk.Tk()
window.geometry("1000x800")
window.title("3Dsquare")
canvas = tk.Canvas(window, width = 2000, height = 800, bg = 'white')
canvas.pack()
window.mainloop()

接下来就要涉及到刚刚的计算公式啦，利用已知参数和变量，来求出需要计算的投射点P’的投射后x和投射后y。
先定义摄像机及投射屏幕平面的位置，这里定义变量名称：
摄像机视点O (cameraX,cameraY,cameraZ)
投射点 (throwX,throwY,throwZ)
实际物体点P (x,y,z)

为了方便计算，我们设：
实际物体平面（绿色平面）与xy轴平面重合
摄像机视点O坐标 (0,0,cameraZ)
投射面A点坐标 (0,0,throwZ)
绿色平面中P点坐标 (x,y,z)
（上面设视点O的xy坐标等于0，是因为OAB垂直于红色绿色平面，将线段OAB在绿色平面的交点B视为坐标原点。）

上文我们说过，投射点P’的z轴坐标可以直接指定，投射后的z坐标只会影响到物体投射出来的大小，可以根据显示情况自行制定，摄像机视点O的z轴坐标也是一样的，可以自己制定，只要保证视点O比投射点P’离得更远就可以，那么这里我们设置：
cameraZ = -300
throwZ = -60
（z轴正方向为绿色屏幕向红色屏幕的反方向，x轴正方向向右，y轴正方向向上，本文所有篇幅以此为标准。）
其他几个变量比如cameraX、cameraY、throwX、throwY也都设好初始值0。

然后建立投射公式自定义函数throw_coord(x,y,z)，意为输入实际物体P点的xyz坐标，函数会运算出投射后的throwX和throwY，求出这两个我们需要的值。
还记得公式吗：
px=ox+[(pz–oz)/(z-oz)*(x-ox)]
py=oy+[(pz-oz)/(z-oz)*(y-oy)]

cameraX = 0
cameraY = 0
cameraZ = -300
throwX = 0
throwY = 0
throwZ = -60
def throw_coord(x, y, z):
    global canvas
    global throwX, throwY
    throwX = cameraX+(throwZ-cameraZ)/(z-cameraZ)*(x-cameraX)
    throwY = cameraY+(throwZ-cameraZ)/(z-cameraZ)*(y-cameraY)

该函数建立好之后，可以求出我们想要的投射点P’的xy坐标了，有了xy坐标我们就可以将它画出来了，在此我们新学习一个函数：
canvas.create_line(起点x, 起点y, 终点x, 终点y, fill=’颜色’, width=粗细)
实际使用样例：
canvas.create_line(0, 0, 100, 100, fill = ‘black’, width = 1, tags = ‘3Dline’�)
#绘制一条线从(0,0)到(100,100)，颜色为黑，粗细为1，标签为’3Dline’。

那么问题来了，这个画直线函数是需要定义起点和终点的，而我们每次运算出来的投射点就是一个点，也就是说我们要把上一次函数运算的投射点作为下一次函数绘画的起点，这就需要变量来帮助我们记录每一次运算的结果，给下一次函数绘画用，所以新增变量：throwoldX、throwoldY。放在函数开头让throwoldX=throwX，是为了保证接下来计算新的throwX时上一次运算结果被记录了下来，然后运行绘制函数我们就可以定义起点为(throwoldX, throwoldY)，终点为(throwX, throwY)。

cameraX = 0
cameraY = 0
cameraZ = -300
throwX = 0
throwY = 0
throwZ = -60
def throw_coord(x, y, z):
    global canvas
    global throwX, throwY
    throwXold = throwX
    throwYold = throwY
    throwX = (x-cameraX)*(throwZ-cameraZ)/(z-cameraZ)+cameraX
    throwY = (y-cameraY)*(throwZ-cameraZ)/(z-cameraZ)+cameraX
    canvas.create_line(throwXold, throwYold, throwX, throwY, fill = 'black', width = 1, tags = '3Dline')

最后我们就要将每个点进行计算投射后的xy坐标，然后按照八面体绘画顺序给画出来。
先建立一个自定义函数throw_point(i)，用来计算八面体个八个点，将之前装有八面体六个点位坐标的列表xList、yList、zList去进行投射后点位的计算，来绘制直线，设置一个形参变量i，用来控制该函数绘画第几个点位的直线，比如运行throw_point(1)：绘画八面体0点到1点的直线。

然后建立一个自定义函数throw_object()，和一个绘制点位顺序列表objectPoint，里面的参数是绘画的点位顺序：0，5，1，4，2，5，3，4，0，1，2，3，0，循环遍历这个点位列表，来将点一个个画出来。

def throw_point(i):
    throw_coord(xList[i], yList[i], zList[i])
objectPoint = [0, 5, 1, 4, 2, 5, 3, 4, 0, 1, 2, 3, 0] # 八面体绘制点位顺序
def throw_object():
    for i in objectPoint:
        throw_point(i)

我们将实际绘制函数throw_object()加入到tkinter界面的mainloop()函数前面，来看看运行效果：<br />（微调代码顺序，将tkinter函数放置最下方，个人习惯，新增运行绘制函数throw_object()在在下方第45行。）

xList = []
yList = []
zList = []
def add_coord_init(x, y, z):
    xList.append(x)
    yList.append(y)
    zList.append(z)

add_coord_init(-40, 0, 40) #0点
add_coord_init(-40, 0, -40) #1点
add_coord_init(40, 0, -40) #2点
add_coord_init(40, 0, 40) #3点
add_coord_init(0, 80, 0) #4点
add_coord_init(0, -80, 0) #5点

cameraX = 0
cameraY = 0
cameraZ = -300
throwX = 0
throwY = 0
throwZ = -60
def throw_coord(x, y, z):
    global canvas
    global throwX, throwY
    throwXold = throwX
    throwYold = throwY
    throwX = (x-cameraX)*(throwZ-cameraZ)/(z-cameraZ)+cameraX
    throwY = (y-cameraY)*(throwZ-cameraZ)/(z-cameraZ)+cameraX
    canvas.create_line(throwXold, throwYold, throwX, throwY, fill = 'black', width = 1, tags = '3Dline')

def throw_point(i):
    throw_coord(xList[i], yList[i], zList[i])

objectPoint = [0, 5, 1, 4, 2, 5, 3, 4, 0, 1, 2, 3, 0] # 八面体绘制点位顺序
def throw_object():
    for i in objectPoint:
        throw_point(i)

import tkinter as tk
window = tk.Tk()
window.geometry("1000x800")
window.title("3Dsquare")
canvas = tk.Canvas(window, width = 1000, height = 800, bg = 'white')
canvas.pack()
throw_object()
window.mainloop()

截屏2022-05-03 19.22.38.png
奇怪，为什么在左上角有个奇怪的图形呢？不是应该在画面中间显示吗？
啊哈，因为tkinter界面原点(0,0)定义在左上角，不在屏幕正中间，那怎么办呢？
只要将绘画函数所有的坐标点加上tkinter画面长宽一般就可以啦～
我们的tkinter界面时设定尺寸为“1000x800”，可参考window.geometry(“1000x800”)这句话，那么修改以下代码即可：

canvas.create_line(throwXold+500, throwYold+400, throwX+500, throwY+400, fill = 'black', width = 1,tags = '3Dline')

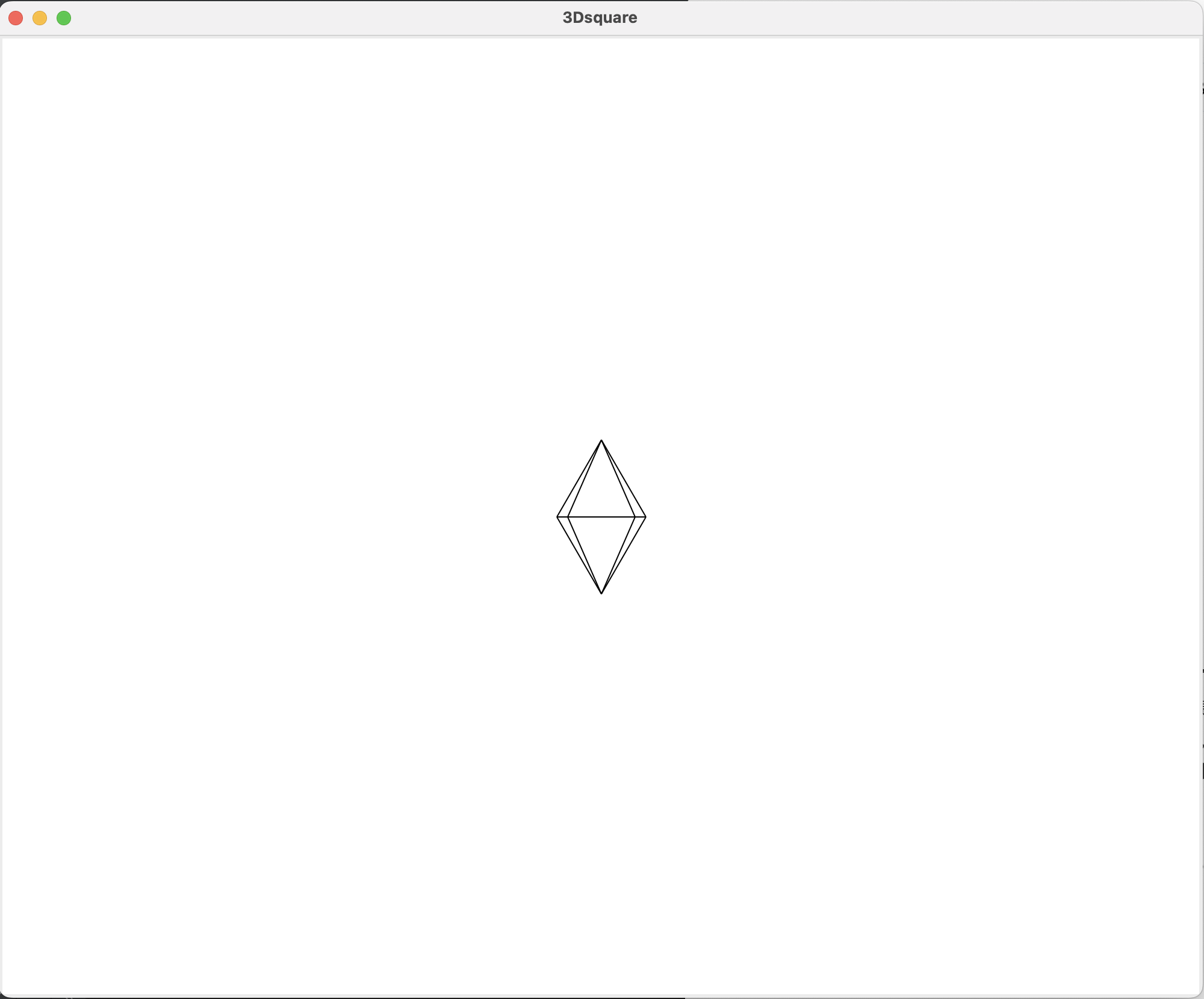
截屏2022-05-04 18.29.03.png
现在我们的八面体就正常显示了，0、1、2、3点由于视角关系重叠成了一条线，但为什么斜线多了两条呢？因为纵深有一个概念叫：近大远小，由于0、3点在后方，1、2点在前方，所以外侧两条线是1、2点与顶点的连线，内侧两条线是0、3点与顶点的连线。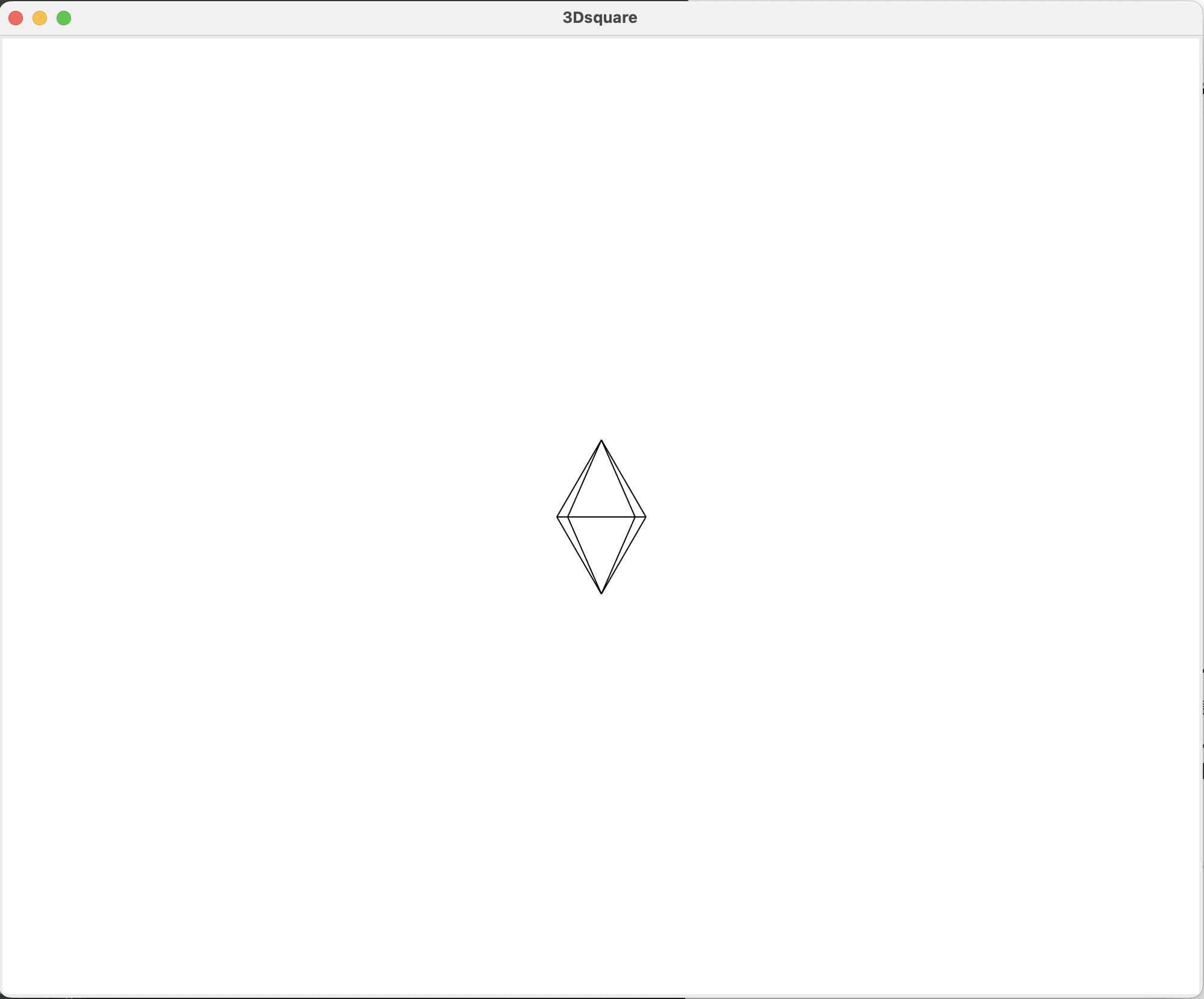
截屏2022-05-04 18.29.03.png
接下来，我们尝试如何让这个八面体移动但视角不动，其实很简单，我们在做的只是将原实际物体的每个点坐标进行投射计算，得到新的投射后的点坐标并连起来，那么移动的话只要将实际物体的坐标改变，那么再经过投射计算，就可以运动起来了。
建立一个移动坐标计算的函数move_coord()，先执行canvas.delete(‘3Dline’)，目的是先将上一条线删除再画新的线，可以看源代码中使用create_line这个函数时，有定义一个tag = ‘3Dline’，意为将这条线绑定一个叫’3Dline’标签，有了这个标签后就可以后期用delete函数删除，函数用法：画布.delete(‘标签’)。
然后执行的操作是一个遍历循环，目的是将xList、yList、zList这三个列表中所有值加上需要移动的量，回顾刚刚说的物体运动其实就是改变实际物体每个点坐标的值，那么只要将这三个列表中的所有坐标值变化就可以移动啦。定义三个形参分别是movedX、movedY、movedZ用来控制移动的量，用i变量遍历xList列表的长度次，遍历过程会把三个列表里的每个值加上movedX、movedY、movedZ，比如：move_coord(0, 100, 0)意为八面体所有点的y坐标向上移动100，最后加入运行投射函数throw_object()。

def move_coord(movedX, movedY, movedZ):
    global canvas
    canvas.delete('3Dline')
    for i in range(len(xList)):
        xList[i] += movedX
        yList[i] += movedY
        zList[i] += movedZ
    throw_object()

我们将上述移动代码在程序最后运行一下，看看效果。

xList = []
yList = []
zList = []
def add_coord_init(x, y, z):
    xList.append(x)
    yList.append(y)
    zList.append(z)

add_coord_init(-40, 20, 40) #0点
add_coord_init(-40, 20, -40) #1点
add_coord_init(40, 20, -40) #2点
add_coord_init(40, 20, 40) #3点
add_coord_init(0, 80, 0) #4点
add_coord_init(0, -80, 0) #5点

cameraX = 0
cameraY = 0
cameraZ = -300
throwX = 0
throwY = 0
throwZ = -60
def throw_coord(x, y, z):
    global canvas
    global throwX, throwY
    throwXold = throwX
    throwYold = throwY
    throwX = (x-cameraX)*(throwZ-cameraZ)/(z-cameraZ)+cameraX
    throwY = (y-cameraY)*(throwZ-cameraZ)/(z-cameraZ)+cameraX
    canvas.create_line(throwXold+500, throwYold+400, throwX+500, throwY+400, fill = 'black', width = 1, tags = '3Dline')

def throw_point(i):
    throw_coord(xList[i], yList[i], zList[i])

objectPoint = [0, 5, 1, 4, 2, 5, 3, 4, 0, 1, 2, 3, 0] # 八面体绘制点位顺序
def throw_object():
    for i in objectPoint:
        throw_point(i)

def move_coord(movedX, movedY, movedZ):
    global canvas
    canvas.delete('3Dline')
    for i in range(len(xList)):
        xList[i] += movedX
        yList[i] += movedY
        zList[i] += movedZ
    throw_object()

import tkinter as tk
window = tk.Tk()
window.geometry("1000x800")
window.title("3Dsquare")
canvas = tk.Canvas(window, width = 1000, height = 800, bg = 'white')
canvas.pack()
move_coord(0,100,0)
window.mainloop()

截屏2022-05-04 22.31.23.png
移动效果实现啦，但为什么左上角多出一条线？
还记得我们画直线的函数是从起点画到终点吗？那么第一次运行画线的起点是哪里呢？是坐标原点(0,0)。因为第一次运行的时候throwoldX和throwoldY是0，想想看是不是这样。
本教程使用的方法是让画线函数第一次不运行，从第二次开始画，这样就避过了从原点画第一条线的问题，新增一个变量drawNum记录绘画次数，每运行一次函数该变量+1，当该变量>0（也就是函数运行第二次）的时候，开始执行画线函数，就可以啦。

cameraX = 0
cameraY = 0
cameraZ = -300
throwX = 0
throwY = 0
throwZ = -60
drawNum = 0
def throw_coord(x, y, z):
    global canvas
    global throwX, throwY, drawNum
    throwXold = throwX
    throwYold = throwY
    throwX = cameraX + (throwZ - cameraZ) / (z - cameraZ) * (x - cameraX)
    throwY = cameraY + (throwZ - cameraZ) / (z - cameraZ) * (y - cameraY)
    if drawNum > 0: # 第一条线起点为（0,0），不画出来
        canvas.create_line(throwXold+500, throwYold+400, throwX+500, throwY+400, fill = 'black', width = 1, tags = '3Dline')
    drawNum += 1

截屏2022-05-04 22.38.12.png
最后，加入物体跟着鼠标移动的方法，首先学习一个如何在tkinter识别鼠标未知的方法：
1、canvas画布绑定鼠标触发事件：canvas.bind(‘‘, mouse_move)
canvas是鼠标跟踪所在画面的画布，名称根据自己程序调整
第一个参数’‘，意为鼠标位置跟踪
�第二个参数mouse_move，意为鼠标一旦移动就跳转该函数
2、创建跳转函数：mouse_move(event)
名称不限，括号内一定要设置形参event用来传递鼠标的位置
mouseX = event.x，将鼠标x坐标放入mouseX中
mouseY = event.y，将鼠标y坐标放入mouseY中

我们新建一个示例程序来测试一下效果：

import tkinter as tk

def mouse_move(event):
    global mouseX, mouseY
    mouseX = event.x - 500 #将原点移到屏幕中心
    mouseY = event.y - 400
    print("鼠标正在释放移动，x："+str(    print("鼠标正在释放移动，x："+str(mouseX)+"，y："+str(mouseY))
mouseX)+"，y："+str(mouseY))

window = tk.Tk()
window.geometry("1000x800")
window.title("test")
canvas = tk.Canvas(window, width = 1000, height = 800, bg = 'white')
canvas.pack()
canvas.bind('<Motion>', mouse_move)
window.mainloop()

屏幕录制2022-05-04 22.57.15.2022-05-04 23_34_42.gif
接下来我们将鼠标事件跳转函数加入程序，并将获得的鼠标xy值除以2，只是为了跟踪范围小一点。

def mouse_move(event):
    global mouseX, mouseY
    mouseX = (event.x - 500)/2
    mouseY = (event.y - 400)/2
    print("鼠标正在释放移动，x："+str(mouseX)+"，y："+str(mouseY))

然后将canvas绑定上鼠标触发事件：canvas.bind(‘‘, mouse_move)。

window = tk.Tk()
window.geometry("1000x800")
window.title("test")
canvas = tk.Canvas(window, width = 1000, height = 800, bg = 'white')
canvas.pack()
canvas.bind('<Motion>', mouse_move)
window.mainloop()

将物体跟踪鼠标运动函数加上循环功能，由于tkinter界面的mainloop机制，导致不能直接在界面运行的同时去进某一个循环，会导致tkinter的界面卡住，那么就要用到tkinter自己的循环方法：after定时插入函数。
canvas.after(8, abc) #after用法：画布.after(ms, 跳转函数)
此条函数意为每定时8ms就跳转一次abc函数

我们新建一个move_loop_3()函数，此函数内部运行移动物体并投射的函数，再加上循环函数。
按照之前讲解的物体运动方法，将获得的mouseX和mouseY代入到函数中，运行：move_coord(mouseX, mouseY, 0)，再加入一个after定时插入函数，跳转的函数就设置为自身函数，这样就相当于做了一个循环，每延时8ms循环一次，after可以赋值成一个变量方便后期进行after中断。
（为什么是延时8ms呢？每移动一步相当于刷新1帧，如果每秒60帧那么延时=1000/60=18ms，每秒120帧=1000/120=8ms）

mouseX = 0
mouseY = 0 # 设置鼠标初始值，以防运行程序时限先执行下方循环程序时并没有移动鼠标，导致mouseX和mouseY并没有值
def move_loop_3D():
    global canvas
    global mouseX, mouseY
    move_coord(mouseX, mouseY, 0)
    after_move_loop_3D = canvas.after(8, move_loop_3D)

最后还要修改一处代码，也是加入鼠标跟踪最关键的地方：move_coord()<br />原本我们这里写的是：xList[i] += movedX，这个movedX是需要移动的量，如果直接运行move_coord(mouseX, mouseY, 0)的话，相当于xList[i] += mouseX，如果鼠标在mouseX=400的地方，也就是说移动的量=400，循环的话物体会不停向右移400不停下来，运行效果是这样的：<br />![屏幕录制2022-05-05 02.00.33.2022-05-05 02_01_45.gif](https://cdn.nlark.com/yuque/0/2022/gif/27295105/1651687322217-9671c9a4-f2bf-4568-b5ab-1a1124b1fb0e.gif#clientId=ue37397de-7cfb-4&crop=0&crop=0&crop=1&crop=1&from=ui&id=uaa4ec746&margin=%5Bobject%20Object%5D&name=%E5%B1%8F%E5%B9%95%E5%BD%95%E5%88%B62022-05-05%2002.00.33.2022-05-05%2002_01_45.gif&originHeight=1964&originWidth=3024&originalType=binary&ratio=1&rotation=0&showTitle=false&size=1862533&status=done&style=none&taskId=u2ebc6ff7-dddb-472d-a185-b30362105fa&title=)<br />�    那么如何让物体能够不停的跟着鼠标但不会一直移动呢？关键就在于移动的量怎么设置。<br />我们来看看移动的量怎么计算：**移动的量=目标位置-当前位置**<br />**当前位置**很好调用，就存放在xList等列表中，如xList[4]提取出来第4个点就是当前位置。<br />**目标位置**不就是鼠标当前的位置嘛？但是这样就会出现一个问题：八面体所有的点汇聚到鼠标一个点上，别忘了我们的xList等列表中放着六个点的坐标，如果都把鼠标的位置当成目标位置，那就会汇聚到鼠标一点上，鼠标的最终位置只是这个八面体最终到达时的中心位置，真正每个点的目标位置还得考虑到八面体的尺寸。<br />我们看下方示意图去理解怎么计算目标位置：<br />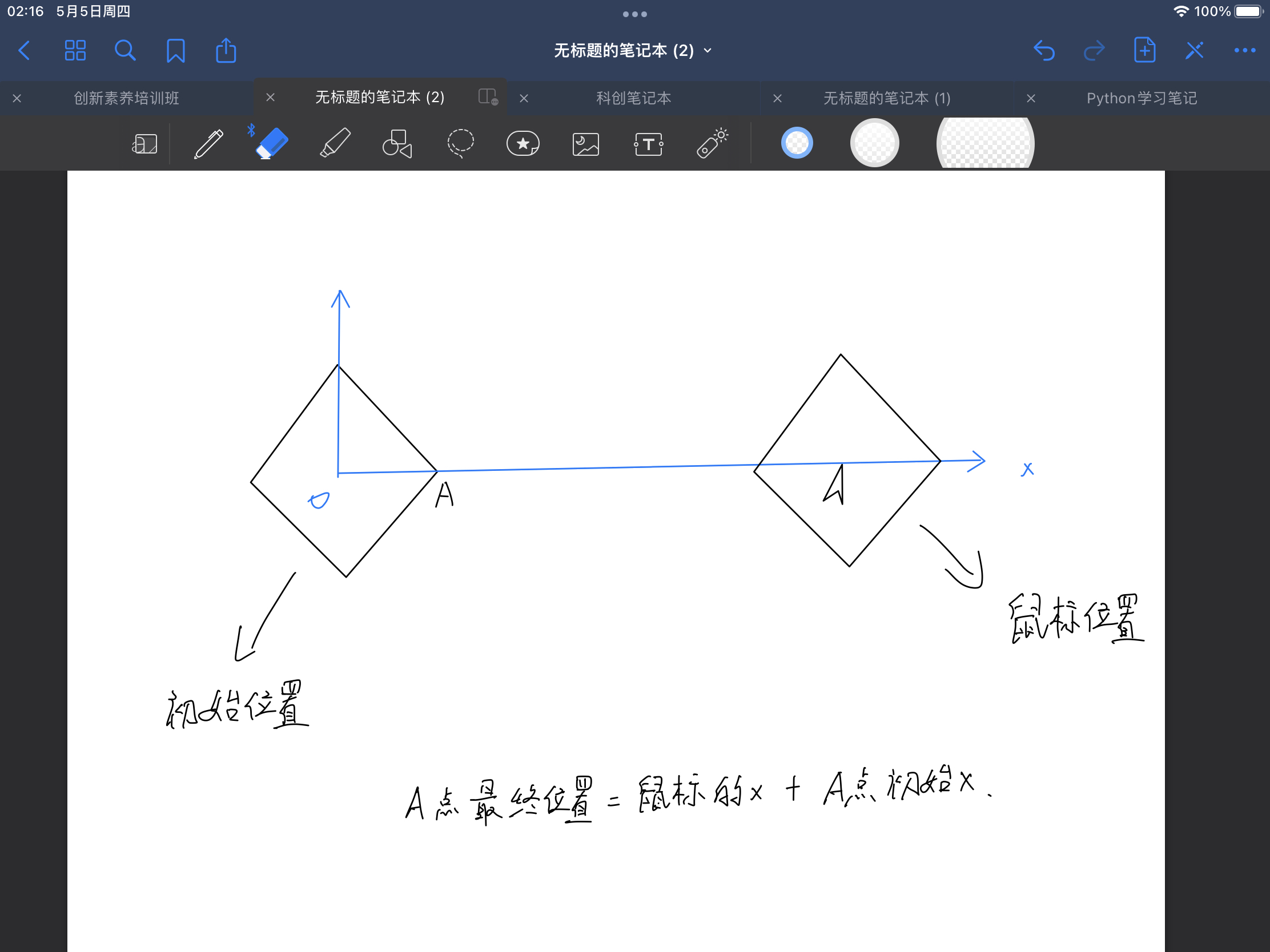![IMG_EB499A589536-1.jpeg](https://cdn.nlark.com/yuque/0/2022/jpeg/27295105/1651688204253-ad1fb1f0-070c-45c1-9d94-7570de2a38eb.jpeg#clientId=ue37397de-7cfb-4&crop=0.1019&crop=0.2752&crop=0.9048&crop=0.8856&from=ui&height=1340&id=u3920fe47&margin=%5Bobject%20Object%5D&name=IMG_EB499A589536-1.jpeg&originHeight=1668&originWidth=2224&originalType=binary&ratio=1&rotation=0&showTitle=false&size=431699&status=done&style=none&taskId=ufdf2dc09-6af0-47df-b595-ff1905ad2bf&title=&width=1786)<br />A点最终位置=鼠标位置+A点初始位置<br />A点初始位置就是当八面体在原点(0,0)时的位置，那么我们看代码如何实现：

先回到最初导入坐标点的函数，新建三个列表：xInitList、yInitList、zInitList，用来存放最一开始出现在坐标原点(0,0)时八面体每个点的位置

xList = []
yList = []
zList = []
xInitList = []
yInitList = []
zInitList = []
def add_coord_init(x, y, z):
    xList.append(x)
    yList.append(y)
    zList.append(z)
    xInitList.append(x)
    yInitList.append(y)
    zInitList.append(z)

回到公式：移动的量=目标位置-当前位置，回到代码移动投射函数，将移动的量加入到其中。
xList[i] += (movedX+xInitList[i]-xList[i])
movedX：在下方调用时会代入mouseX
xinitList[i]：就是最初始的八面体位置
xList[i]：就是八面体当前位置
用这样一个公式就可以使八面体跟踪鼠标而不会一直不停移动了，移动量除以40为了减缓速度和非线性效果。

def move_coord(movedX, movedY, movedZ):
    global canvas
    canvas.delete('3Dline')
    for i in range(len(xList)):
        xList[i] += (movedX+xInitList[i]-xList[i])/40
        yList[i] += (movedY+yInitList[i]-yList[i])/40
        zList[i] += movedZ
    throw_object()

move_coord(mouseX, mouseY, 0)

最最后，整合代码，别忘了在函数下方调用move_loop_3D()使其循环，查看移动效果。<br />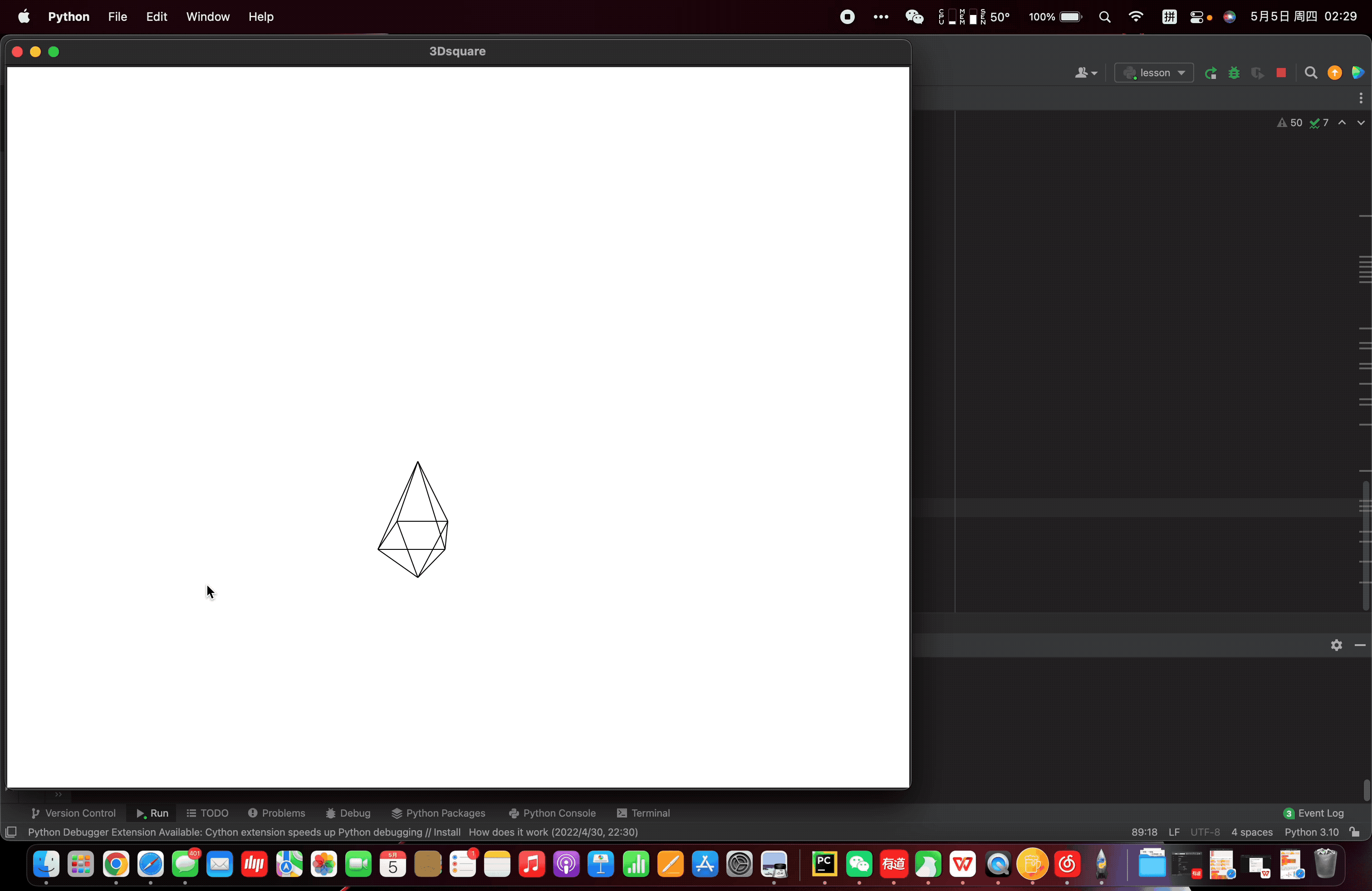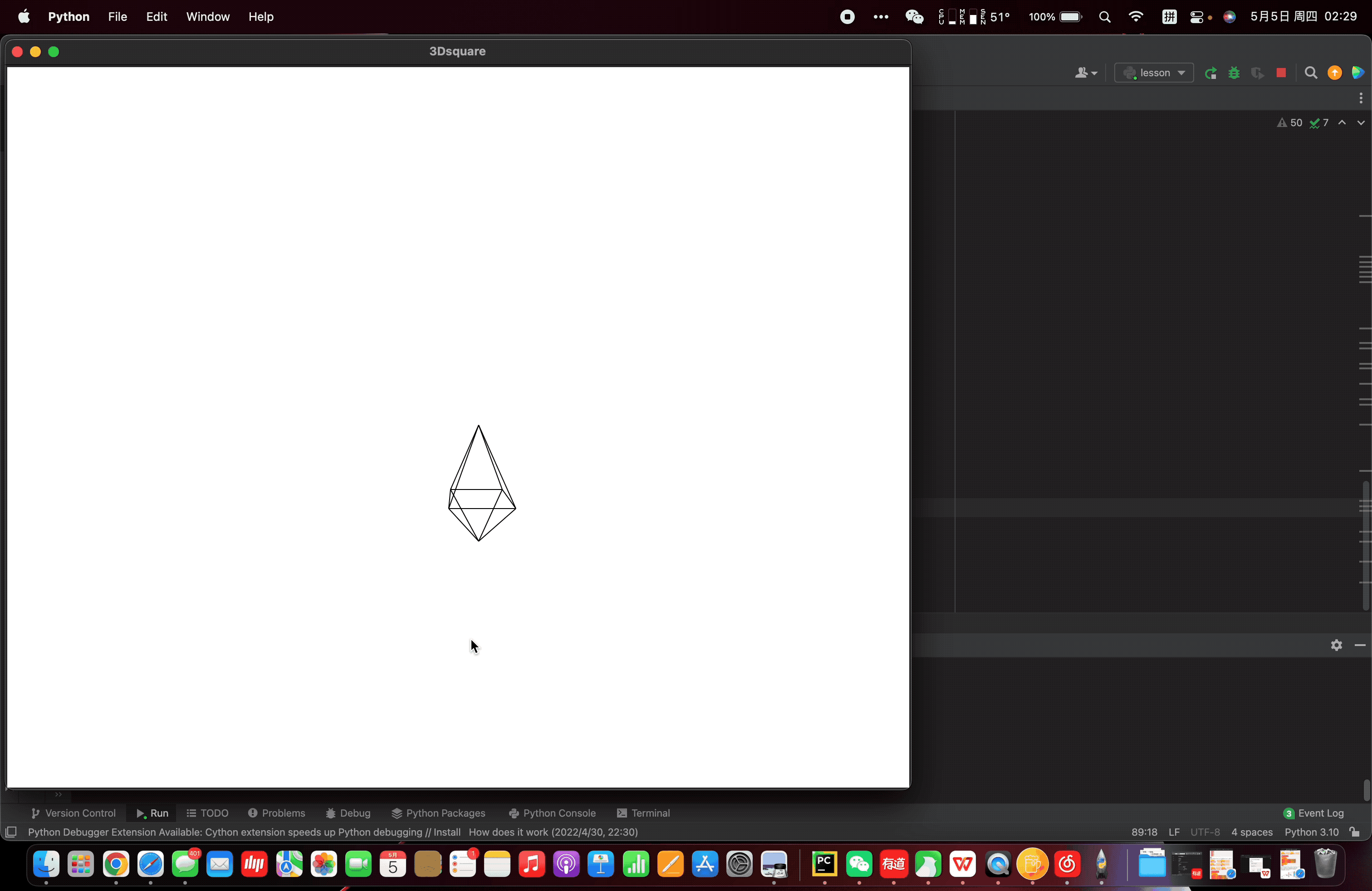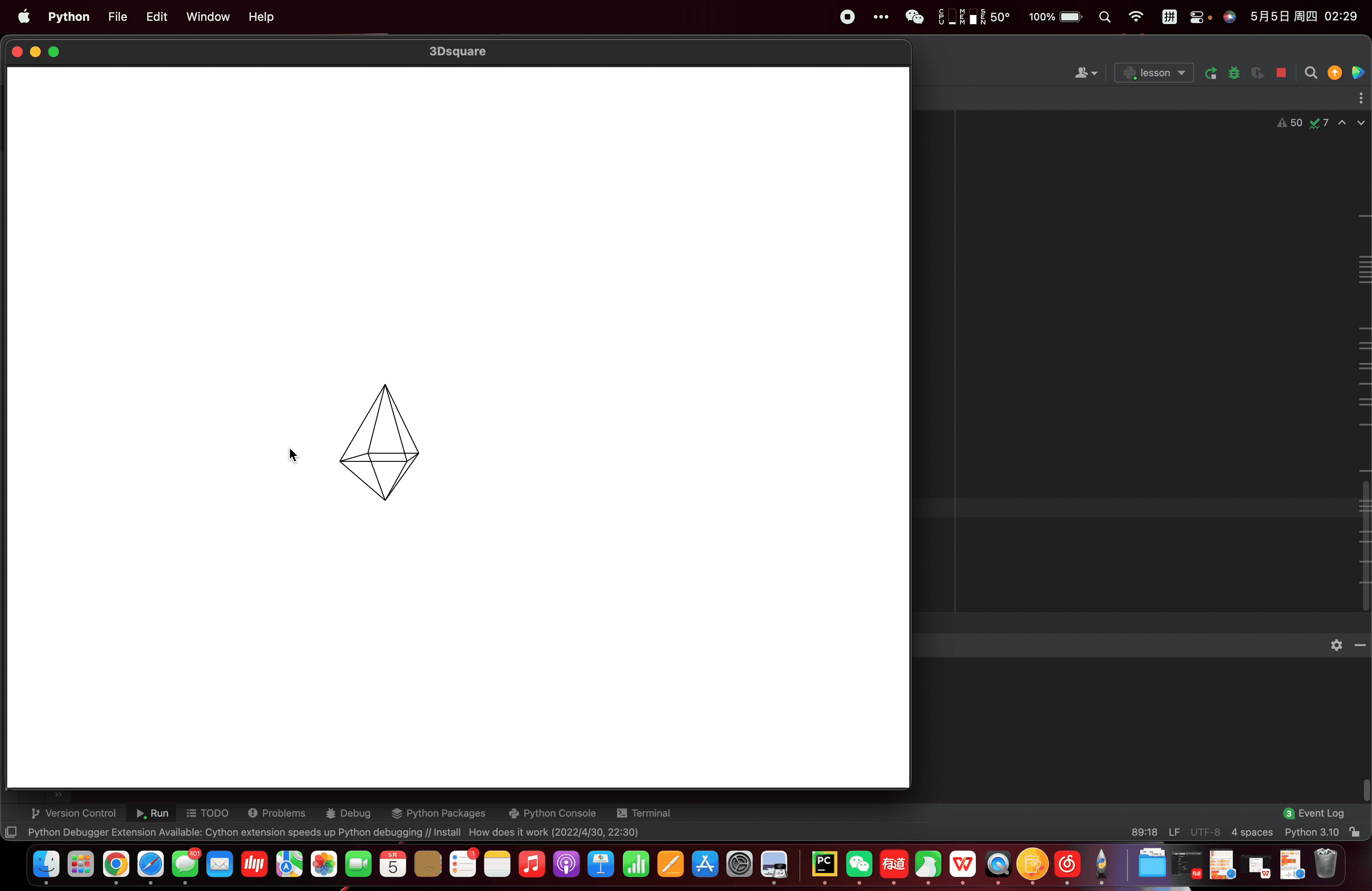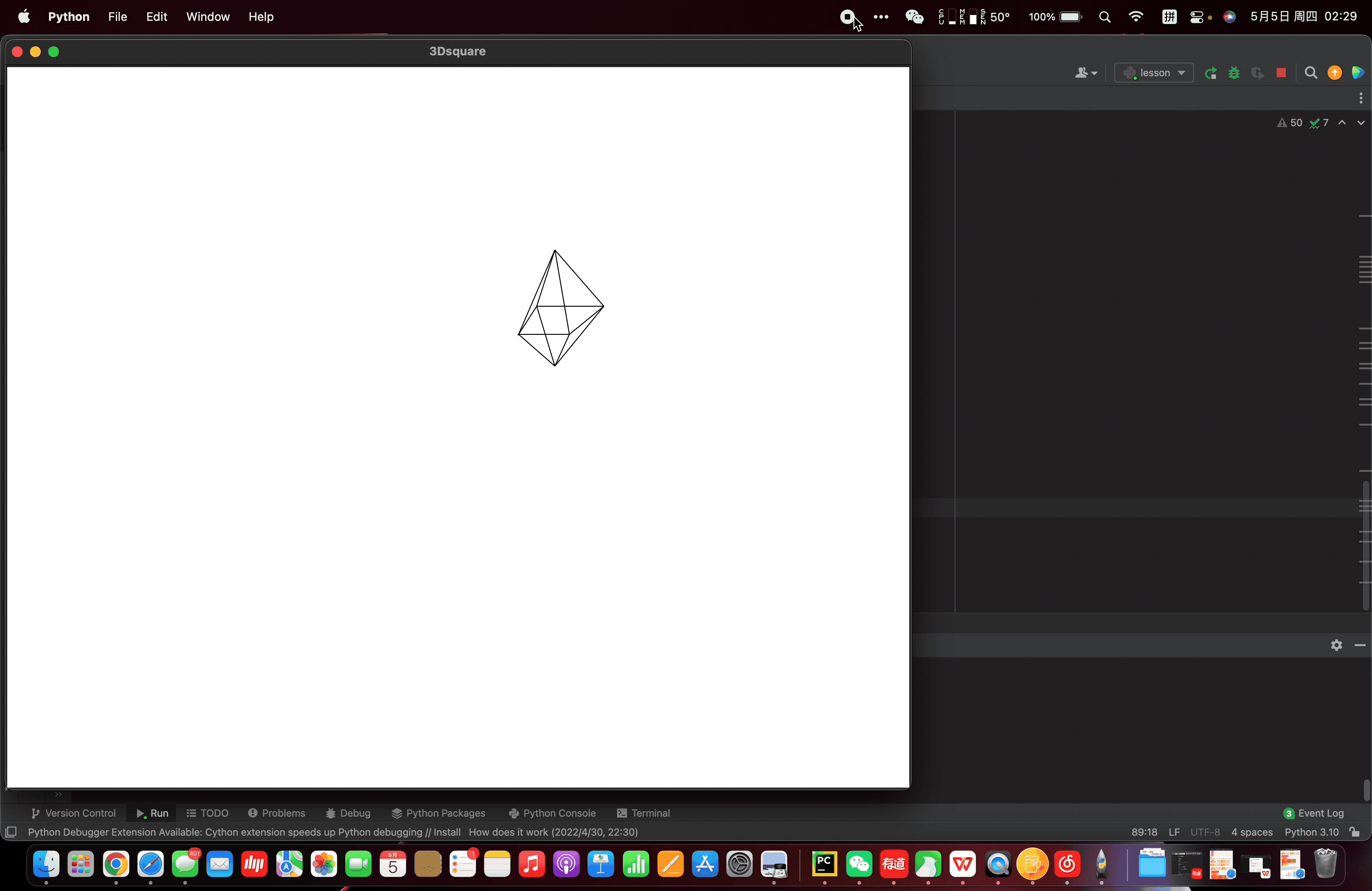![屏幕录制2022-05-05 02.29.13.2022-05-05 02_37_15.gif](https://cdn.nlark.com/yuque/0/2022/gif/27295105/1651689449005-ab0fb4e2-ad3a-49a2-a61f-88d37b1885f5.gif#clientId=ue37397de-7cfb-4&crop=0&crop=0&crop=1&crop=1&from=ui&id=ZdB7l&margin=%5Bobject%20Object%5D&name=%E5%B1%8F%E5%B9%95%E5%BD%95%E5%88%B62022-05-05%2002.29.13.2022-05-05%2002_37_15.gif&originHeight=1964&originWidth=3024&originalType=binary&ratio=1&rotation=0&showTitle=false&size=4021643&status=done&style=none&taskId=ua7c62c06-f30d-41a4-b997-efe3569b09b&title=)

xList = []
yList = []
zList = []
xInitList = []
yInitList = []
zInitList = []
def add_coord_init(x, y, z):
    xList.append(x)
    yList.append(y)
    zList.append(z)
    xInitList.append(x)
    yInitList.append(y)
    zInitList.append(z)

add_coord_init(-40, 20, 40) #0点
add_coord_init(-40, 20, -40) #1点
add_coord_init(40, 20, -40) #2点
add_coord_init(40, 20, 40) #3点
add_coord_init(0, 80, 0) #4点
add_coord_init(0, -80, 0) #5点

cameraX = 0
cameraY = 0
cameraZ = -300
throwX = 0
throwY = 0
throwZ = -60
drawNum = 0
def throw_coord(x, y, z):
    global canvas
    global throwX, throwY, drawNum
    throwXold = throwX
    throwYold = throwY
    throwX = cameraX + (throwZ - cameraZ) / (z - cameraZ) * (x - cameraX)
    throwY = cameraY + (throwZ - cameraZ) / (z - cameraZ) * (y - cameraY)
    if drawNum > 0: # 第一条线起点为（0,0），不画出来
        canvas.create_line(throwXold+500, throwYold+400, throwX+500, throwY+400, fill = 'black', width = 1, tags = '3Dline')
    drawNum += 1

def throw_point(i):
    throw_coord(xList[i], yList[i], zList[i])

objectPoint = [0, 5, 1, 4, 2, 5, 3, 4, 0, 1, 2, 3, 0] #八面体绘制点位顺序
def throw_object():
    for i in objectPoint:
        throw_point(i)

def move_coord(movedX, movedY, movedZ):
    global canvas
    canvas.delete('3Dline')
    for i in range(len(xList)):
        xList[i] += (movedX+xInitList[i]-xList[i])/40
        yList[i] += (movedY+yInitList[i]-yList[i])/40
        zList[i] += movedZ
    throw_object()

def mouse_move(event):
    global mouseX, mouseY
    mouseX = (event.x - 500)/2
    mouseY = (event.y - 400)/2
    print("鼠标正在释放移动，x："+str(mouseX)+"，y："+str(mouseY))

mouseX = 0
mouseY = 0 # 设置鼠标初始值，以防运行程序时限先执行下方循环程序时并没有移动鼠标，导致mouseX和mouseY并没有值
def move_loop_3D():
    global canvas
    global mouseX, mouseY
    move_coord(mouseX, mouseY, 0)
    after_move_loop_3D = canvas.after(8, move_loop_3D)

import tkinter as tk
window = tk.Tk()
window.geometry("1000x800")
window.title("3Dsquare")
canvas = tk.Canvas(window, width = 1000, height = 800, bg = 'white')
canvas.pack()
canvas.bind('<Motion>', mouse_move)
move_loop_3D()
window.mainloop()

那么如何做出多个物体，或者是正方体移动呢？自己尝试做下吧，成功了你就会了。

本期教程结束，可以自己尝试制作正方体互动+多个物体～
源代码文件：3DTest.py