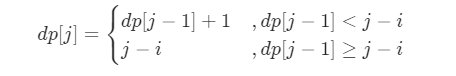- 剑指 Offer 10- I. 斐波那契数列">剑指 Offer 10- I. 斐波那契数列
- 剑指 Offer 10- II. 青蛙跳台阶问题">剑指 Offer 10- II. 青蛙跳台阶问题
- 剑指 Offer 42. 连续子数组的最大和">剑指 Offer 42. 连续子数组的最大和
- 剑指 Offer 47. 礼物的最大价值
">剑指 Offer 47. 礼物的最大价值 - 剑指 Offer 48. 最长不含重复字符的子字符串">剑指 Offer 48. 最长不含重复字符的子字符串
- 剑指 Offer 49. 丑数">剑指 Offer 49. 丑数
- 剑指 Offer 60. n个骰子的点数(?)">剑指 Offer 60. n个骰子的点数(?)
- 剑指 Offer 66. 构建乘积数组
">剑指 Offer 66. 构建乘积数组
剑指 Offer 10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。 答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。 示例 1: 输入:n = 2 输出:1 |
|---|
题解思路:只使用两个变量实现
class Solution {public int fib(int n) {int a = 0, b = 1, sum;for (int i = 0; i < n; i++) {sum = (a + b) % 1000000007;a = b;b = sum;}return a;}}
题解思路:使用dp[ ]表实现
class Solution {public int fib(int n) {if (n == 0) return 0;int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];dp[i] %= 1000000007;}return dp[n];}}
剑指 Offer 10- II. 青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。 示例 1: 输入:n = 2 输出:2 |
|---|
题解思路:在每一阶台阶上,青蛙都有两个选择:要么是跳一阶,要么是跳两阶。
class Solution {public int numWays(int n) {if (n == 0) return 1;int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];dp[i] %= 1000000007;}return dp[n];}}
题解思路:使用两个变量来实现
class Solution {public int numWays(int n) {int a = 1, b = 1, sum;for (int i = 2; i <= n; i++) {sum = (a + b) % 1000000007;a = b;b = sum;}return b;}}
剑指 Offer 42. 连续子数组的最大和
| 输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。 要求时间复杂度为O(n)。 示例1: 输入: nums = [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。 |
|---|
转移方程: 若 dp[i-1] \leq 0dp[i−1]≤0 ,说明 dp[i - 1]dp[i−1] 对 dp[i]dp[i] 产生负贡献,即 dp[i-1] + nums[i]dp[i−1]+nums[i] 还不如 nums[i]nums[i] 本身大。
- 当 dp[i - 1] > 0 时:执行 dp[i] = dp[i-1] + nums[i] ;
- 当dp[i−1]≤0 时:执行 dp[i] = nums[i] ;
class Solution { public int maxSubArray(int[] nums) { int res = nums[0]; for(int i = 1; i < nums.length; i++) { nums[i] += Math.max(nums[i - 1], 0); res = Math.max(res, nums[i]); } return res; } }public int maxSubArray(int[] nums) { int max = nums[0]; int former = 0;//用于记录dp[i-1]的值,对于dp[0]而言,其前面的dp[-1]=0 int cur = nums[0];//用于记录dp[i]的值 for(int num:nums){ cur = num; if(former>0) cur +=former; if(cur>max) max = cur; former=cur; } return max; }public int maxSubArray(int[] nums) { int[] dp = new int[nums.length]; dp[0] = nums[0]; int max = dp[0]; for (int i = 1; i < nums.length; i++) { dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]); max = Math.max(max, dp[i]); } return max; }
剑指 Offer 47. 礼物的最大价值
| 在一个 mn 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物? 示例 1: 输入: [[1,3,1], [1,5,1], [4,2,1] ] 输出: 12*解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物 |
|---|
题解思路:
设f(i,j)为从棋盘左上角走至单元格(i,j)的礼物最大累计价值,易得到以下递推关系:f(i,j)等于f(i,j-1)和f(i-1,j)中的较大值加上当前单元格礼物价值grid(i,j)。
f(i,j)=max[f(i,j−1),f(i−1,j)]+grid(i,j)
动态规划解析:**
- 状态定义: 设动态规划矩阵 dp ,dp(i,j) 代表从棋盘的左上角开始,到达单元格 (i,j)时能拿到礼物的最大累计价值。
- 转移方程:

- 初始状态: dp[0][0] = grid[0][0] ,即到达单元格 (0,0) 时能拿到礼物的最大累计价值为 grid[0][0];
- 返回值: dp[m-1][n-1] ,m, n 分别为矩阵的行高和列宽,即返回 dp 矩阵右下角元素。
public int maxValue(int[][] grid) { int m = grid.length, n = grid[0].length; for (int i = 1; i < m; i++) //初始化第一列 grid[i][0] += grid[i - 1][0]; for (int j = 1; j < n; j++) // 初始化第一行 grid[0][j] += grid[0][j - 1]; for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { grid[i][j] += Math.max(grid[i - 1][j], grid[i][j-1]); } } return grid[m - 1][n - 1]; }总结: 1、我们可以发现状态转移方程其实都在上一步的前提下寻找最优解
优化思路:
多开一行一列的空间
public int maxValue(int[][] grid) {
int row = grid.length, column = grid[0].length;
int[][] dp = new int[row + 1][column + 1];
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= column; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
}
}
return dp[row][column];
}
注意:dp与grid的对应关系 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
剑指 Offer 48. 最长不含重复字符的子字符串
| 请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。 示例 1: 输入: “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 |
|---|
题解思路
长度为N的字符串共有N(N+1)/2个子字符串(复杂度为O(N)),判断长度为N的字符串是否具有重复字符的复杂度为O(N),因此本题使用暴力解法的复杂度为O(N).考虑使用动态规划降低时间复杂度。
动态规划解析
- 状态定义:设动态规划列表dp,dp[j]代表以字符s[j]为结尾的“最长不重复子字符串”的长度。
- 转移方程:固定右边界j,设字符s[j]左边距离最近的相同字符为s[i],即s[i]=s[j]。
1、当i<0,即s【j】左边无相同字符,则dp【j】=dp【j-1】+1;
2、当dp【j-1】
当i<0时,由于dp【j-1】<=j恒成立,因而dp【j-1】<j-i恒成立,因此分支1、2可以合并。
- 返回值:max(dp),即全局的“最长不重复子字符串”的长度
方法一:动态规划+哈希表
- 哈希表统计:遍历字符串s时, 使用哈希表(记为dic)统计各字符最后一次出现的索引位置。
- 左边界 i 获取方式:遍历到s【j】时,可通过访问哈希表dic[ s[j] ]获取最近的相同字符的索引 i 。
class Solution { public int lengthOfLongestSubstring(String s) { Map<Character, Integer> dic = new HashMap<>(); int res = 0, tmp = 0; for (int j = 0; j < s.length(); j++) { int i = dic.getOrDefault(s.charAt(j), -1);//获取索引 i (即当前元素的左边界,不存在则为-1) dic.put(s.charAt(j), j);//更新哈希表 tmp = tmp < j - i ? tmp + 1 : j - i; res = Math.max(res, tmp);//max(dp[j-1],dp[j]) } return res; } }
方法二:动态规划+线性遍历
- 左边界 i 获取方式: 遍历到 s[j]时,初始化索引 i = j - 1 ,向左遍历搜索第一个满足 s[i] = s[j]的字符即可 。
public int lengthOfLongestSubstring(String s) { Map<Character, Integer> dic = new HashMap<>(); int res = 0, tmp = 0; for (int j = 0; j < s.length(); j++) { int i = j - 1; while (i >= 0 && s.charAt(i) != s.charAt(j)) i--; tmp = tmp < j - i ? tmp + 1 : j - i; res = Math.max(res, tmp); } return res; }
方法三:双指针+哈希表
- 哈希表 dic 统计: 指针 j 遍历字符 s ,哈希表统计字符 s[j] 最后一次出现的索引 。
- 更新左指针 i : 根据上轮左指针 i 和 dic[s[j]] ,每轮更新左边界 i ,保证区间 [i + 1, j] 内无重复字符且最大。
i=max(dic[s[j]],i) (这里获取较大值的原因在于不让左指针回到更前的情况出现)
- 更新结果 res : 取上轮 res 和本轮双指针区间 [i + 1,j] 的宽度(即 j - i )中的最大值。
res=max(res,j−i)
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> dic = new HashMap<>();
int i = -1, res = 0;
for (int j = 0; j < s.length(); j++) {
if (dic.containsKey(s.charAt(j)))
i = Math.max(i, dic.get(s.charAt(j)));
dic.put(s.charAt(j), j);
res = Math.max(res, j - i);//更新结果(左开右闭区间)
}
return res;
}
总结: 1、不可以简单的通过循环一个元素的那样去寻找上一个元素的位置然后比较得到最大值,这样的做法错误点在于,左右边界内部可能会出现重复的情况。 2、为了防止上述1的问题出现,我们需要不断的控制左边界的位置。 3、只有出现相同元素的情况才会更新左边界
剑指 Offer 49. 丑数
| 我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。 示例: 输入: n = 10 输出: 12 解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。 |
|---|
题解思路:
丑数的递推性质:丑数只包含因子2,3,5,因此有:丑数=某较小丑数 x 某因子
设已知长度为n的丑数序列x,x,…,x,求第n+1个丑数x。根据递推性质,丑数x只可能是以下三种情况之一
x=x x 2 || xx 3 || xx 4
class Solution {
public int nthUglyNumber(int n) {
int[] dp = new int[n]; // 使用dp数组来存储丑数序列
dp[0] = 1; // dp[0]已知为1
int a = 0, b = 0, c = 0; // 下个应该通过乘2来获得新丑数的数据是第a个, 同理b, c
for(int i = 1; i < n; i++){
// 第a丑数个数需要通过乘2来得到下个丑数,第b丑数个数需要通过乘2来得到下个丑数,同理第c个数
int n2 = dp[a] * 2, n3 = dp[b] * 3, n5 = dp[c] * 5;
dp[i] = Math.min(Math.min(n2, n3), n5);
if(dp[i] == n2){
a++; // 第a个数已经通过乘2得到了一个新的丑数,那下个需要通过乘2得到一个新的丑数的数应该是第(a+1)个数
}
if(dp[i] == n3){
b++; // 第 b个数已经通过乘3得到了一个新的丑数,那下个需要通过乘3得到一个新的丑数的数应该是第(b+1)个数
}
if(dp[i] == n5){
c++; // 第 c个数已经通过乘5得到了一个新的丑数,那下个需要通过乘5得到一个新的丑数的数应该是第(c+1)个数
}
}
return dp[n-1];
}
}
总结: 在已有的丑数序列上每一个数都必须乘2, 乘3, 乘5, 这样才不会漏掉某些丑数。假设已有的丑数序列为[1, 2, 3, …, n1, n2], 如果单纯的让每个丑数乘2, 乘3, 乘5顺序排列的话肯定会有问题, 比如如果按照这样的顺序排列下去肯定有问题[12, 13, 15, 22, 23, 25, 32, 33, 35, … , n1 2, n1 3, n1 5, n2 2, n3 3, n2 * 5],因为后面乘2的数据可能会比前面乘3乘5的数据要小,那这个乘2的数应该排在他们的前面, 后面乘3的数据也可能比前面乘5的数据要小,那这个乘3的数应该排在他们的前面。 那怎么办呢,每个数都必须乘2, 乘3, 乘5这样才能保证求出所有的丑数,而且还要保证丑数的顺序,这个改如何同时实现呢? 通过观察网上的各个题解,终于找到了办法,那就是记录每个丑数是否已经被乘2, 乘3, 乘5了, 具体的做法是 设置3个索引a, b, c,分别记录前几个数已经被乘2, 乘3, 乘5了,比如a表示前(a-1)个数都已经乘过一次2了,下次应该乘2的是第a个数;b表示前(b-1)个数都已经乘过一次3了,下次应该乘3的是第b个数;c表示前(c-1)个数都已经乘过一次5了,下次应该乘5的是第c个数;
剑指 Offer 60. n个骰子的点数(?)
| 把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。 你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。 示例 1: 输入: 1 输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667] |
|---|
题解思路1:
以三个骰子为例:三个骰子掷出4的概率等于两个骰子掷出1的概率乘一个骰子掷出3的概率+两个骰子掷出2的概率乘一个骰子掷出1的概率……….利用动态规划的思路,使用dp[ n ][ k ]表示n个骰子掷出k点的概率。
则dp[3][4] = dp[2][1] * dp[1][3] + dp[2][2] * dp[1][2] + dp[2][3] * dp[1][1]。
动态规划: 1、构造一个dp数组:dp[i][j] 表示:当有i个骰子时,掷出和为 j 的几率 2、初始化一个骰子的情况 3、动态规划计算其他情况 推导方程: 有 i 个骰子,掷出和为 j 的可能性==(有一个骰子,掷出和为1-6的可能性)=(有i-1 个骰子掷出和为 j -(1-6)的可能性) dp[ i ][ j ]+=dp[1][ k ]dp[i-1][ j-k ];
class Solution {
public double[] dicesProbability(int n) {
//dp[n][k] 表示n个骰子掷出k点数的概率
double[][] dp = new double[n + 1][n * 6 + 1];
for (int i = 1; i <= 6; i++) { //初始化1个骰子的情况
dp[1][i] = (double) 1 / 6;
}
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= 6 * i; j++) { //注意次数j的最大值
for (int k = 1; k <= 6; k++) { //此处的循环代表只有一个骰子的情况,所以值是从1到6;
if (j - k < 1) //剔除不符合条件的情况
continue;
dp[i][j] += dp[1][k] * dp[i - 1][j - k]; //动态规划
}
}
}
double[] res = new double[5 * n + 1];
int id = n;
for (int i = 0; i < res.length; i++) {
res[i] = dp[n][id++];
}
return res;
}
}
题解思路2:
1、构造dp数组,tmp[ ]为n个骰子的点数概率数据,pre[ ]为n-1个骰子的点数概率数组,一个骰子的点数概率数组显然是6个1/6,不需要另外设置数组 2、初始化dp数组:pre[ ]={ 1/6d,1/6d,1/6d,1/6d,1/6d,1/6d} 3、构造状态转移方程:tmp[x+y]=pre[x]*nums[y];
class Solution {
public double[] dicesProbability(int n) {
double[] pre = {1 / 6d, 1 / 6d, 1 / 6d, 1 / 6d, 1 / 6d, 1 / 6d};
for (int i = 2; i <= n; i++) {
double[] tmp = new double[5 * i + 1];
for (int j = 0; j < pre.length; j++) {
for (int x = 0; x < 6; x++) {
tmp[j + x] += pre[j] * ((double) 1 / 6); //注意此处的1/6的概率其实就是一个骰子的概率
}
}
pre = tmp;
}
return pre;
}
}
剑指 Offer 66. 构建乘积数组
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。示例: 输入: [1,2,3,4,5] 输出: [120,60,40,30,24] |
|---|
题解思路:
本题的难点在于不能使用除法,即需要只用乘法生成B数组。根据题目对B [ i ]的定义,可列出表格,因为是除去 i 本身以外的其他元素的乘积,所以我们在计算的过程中可以将 i 的元素的值设定为 1。通过上三角与下三角的方式将双重循环遍历转换为两个单层循环遍历。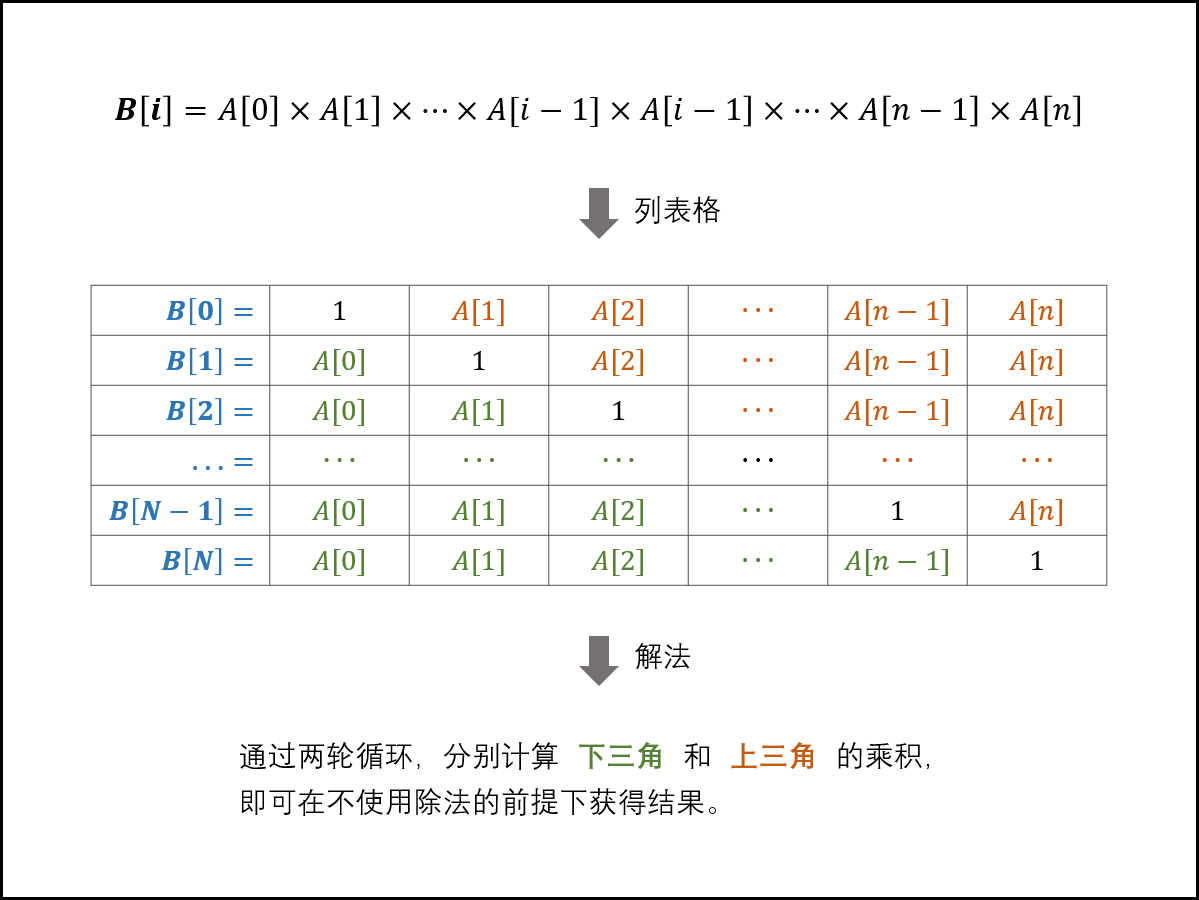
算法流程: 1、初始化:数组B,其中B【0】=1;辅助变量tmp=1; 2、计算B[ i ]的下三角各元素 的乘积,直接乘入B【i】; 3、计算 B[i]的 上三角 各元素的乘积,记为 tmp ,并乘入 B[i] ; 4、返回 B。
class Solution {
public int[] constructArr(int[] a) {
if (a.length == 0)
return new int[0];
int[] b = new int[a.length];
b[0] = 1;
int tmp = 1;
for (int i = 1; i < a.length; i++) { //下三角
b[i] = b[i - 1] * a[i - 1];
}
for (int i = a.length - 2; i >= 0; i--) { //上三角
tmp *= a[i + 1];
b[i] *= tmp;
}
return b;
}
}
本质就是两个dp数组,分别维护 i 左侧、 右侧的乘积和,
public int[] constructArr(int[] a) {
if (a == null || a.length == 0) return a;
int len = a.length;
int[] left = new int[len];
int[] right = new int[len];
left[0] = right[len - 1] = 1;
for (int i = 1; i < len; i++) {
left[i] = left[i - 1] * a[i - 1];
}
for (int i = len - 2; i >= 0; i--) {
right[i] = right[i + 1] * a[i + 1];
}
int[] ans = new int[len];
for (int i = 0; i < len; i++) {
ans[i] = left[i] * right[i];
}
return ans;
}
单层循环,两边同时进行
public int[] constructArr(int[] a) {
if (a == null || a.length == 0) {
return a;
}
int len = a.length;
int[] b = new int[len];
int left = 1, right = 1;
Arrays.fill(b, 1);
for (int i = 0; i < len; i++) {
b[i] *= left;
left *= a[i];
b[len - i - 1] *= right;
right *= a[len - i - 1];
}
return b;
}