1.2 分治递归求解

递归是一种基本的算法设计方法，而递归算法的代价往往可以用递归方程来描述，因而解递归方程就成为递归算法分析的重要技术。

1. 替换法

有一种“大胆假设，小心求证”的方法可以帮助解递归方程，其核心原理是，如果能够猜测递归式的一个解，我们往往可以采用所谓替换法来较容易地证明它。替换法的本质是数学归纳法。

例：求解递归式 . 首先，我们猜测 ，然后证明。 即证明对于某个常数 对于充分大的 成立。 按照数学归纳法，我们假设对于小于 的情况，已经成立，基于归纳假设，有 ，所以，

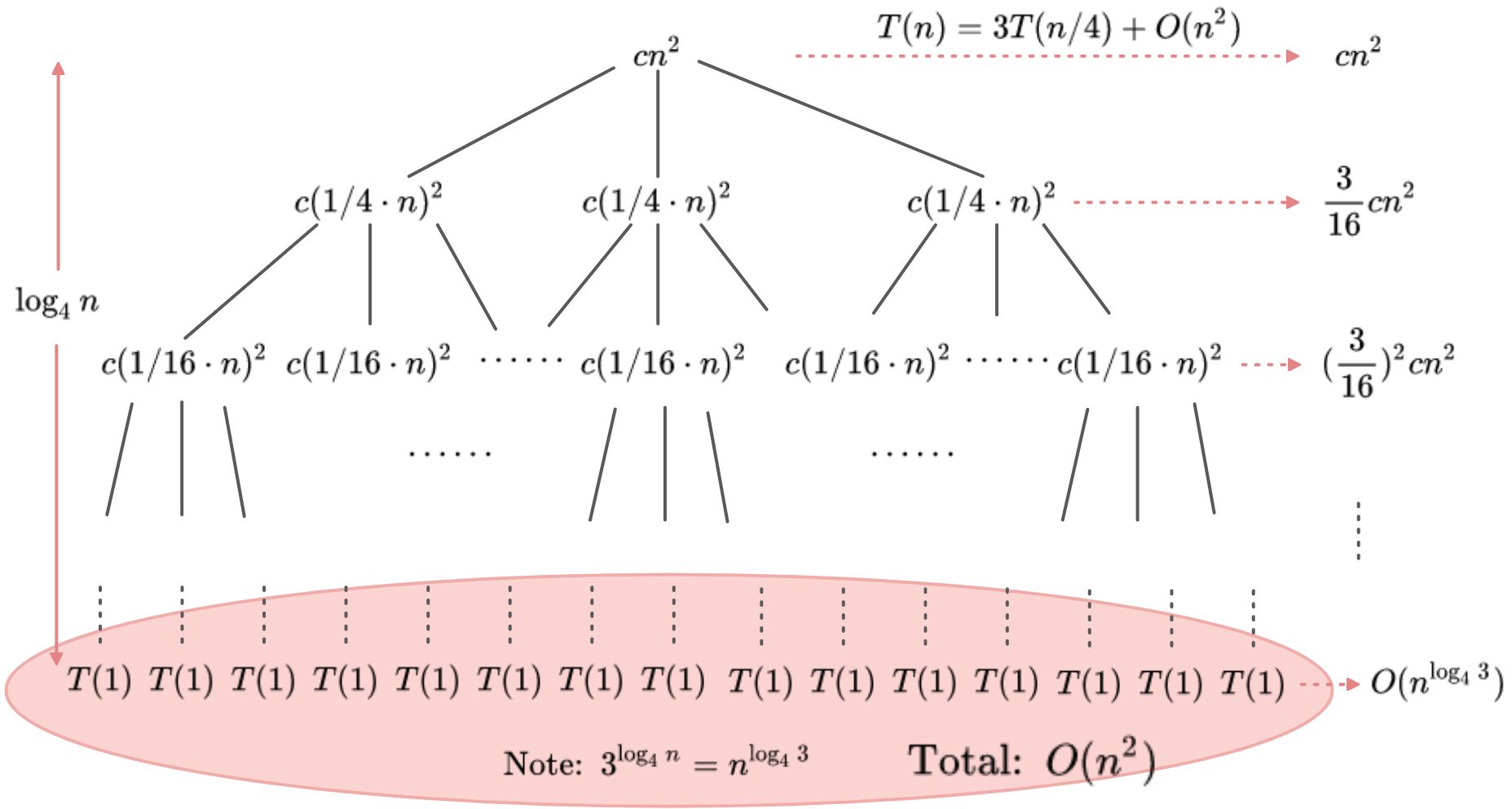
2. 递归树

分治算法的形式一般是将原始问题分解为若干小问题，每个小问题递归求解，再将小问题的解合并成原始问题的解。根据这一过程，分治递归具有如下一般形式：

这里称 为非递归代价。

3. Master 定理