2.1 分治排序

分治策略的两个关键步骤是子问题的划分和子问题解的合并。根据这两个步骤的难易程度，一般有两类典型的分治算法：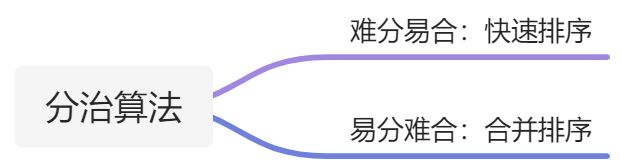

分治排序将蛮力排序 的时间复杂度改进到了 。

1. 快速排序

1.1 插入排序的不足

插入排序基于遍历来实现的，它的最坏和平均情况时间复杂度均为 。

思考：插入排序改进的空间在哪里？哪些计算是多余的？如何减少？

1.1.1 逆序对

为了可以通过更有力的数学工具来深入分析插入排序的不足，这里引入逆序对的概念。

定义 （逆序对）给定一组各不相同的两两可比较的元素。对于这些元素的一个排列 而言，定义二元组 为一个逆序对，如果 ，且 。

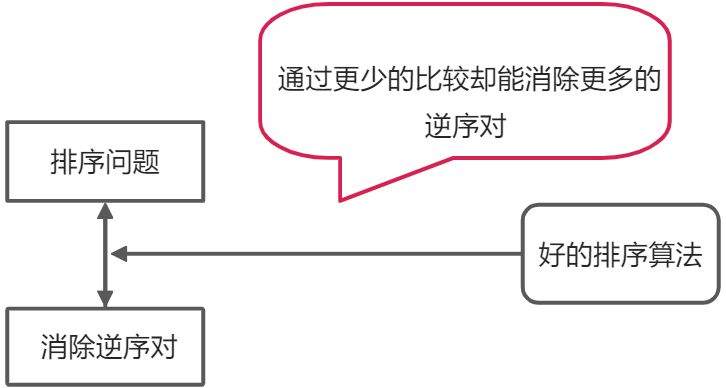
基于逆序对的概念，可以等价地换一个视角来描述排序问题和排序算法。

对于输入的待排序元素的序列，它包含若干个逆序对，而排序算法就是通过元素的比较，调整元素的位置，消除输入序列中的逆序对。

从消除逆序对的角度来看插入排序的一个关键特征：每次总是将相邻的元素进行比较，至多只能消除序列中的一个逆序对。

1.1.2 插入排序时间复杂度分析

最坏情况下：
对于一个从大到小排列的输入序列，其中任意两个元素均构成逆序对，所以最坏情况下输入序列中可能有 个逆序对。
平均情况下：
假设所有可能的输入等概率地出现，平均情况下逆序对的个数就是输入序列中所有二元组个数的一半，即

基于以上分析，插入排序的主要问题是一次比较至多只能消除一个逆序对。后续改进的出发点就是如何更“聪明”地进行元素的比较，使得一次比较能够消除更多的逆序对。

1.2 快速排序的改进

1.2.1 快速排序算法的基本原理

1.2.2 快速排序算法

1.3 最坏情况时间复杂度分析

1.4 平均情况时间复杂度分析

1.4.1 基于递归方程

1.4.2 基于指标随机变量

2. 合并排序

合并排序的最坏情况时间复杂度满足：

根据 Master 定理有 。

3. 基于比较的排序的下界