四、LU与置换矩阵

一、知识概要

这一节中首先完善之前讲到的逆矩阵内容，然后使用消元矩阵介绍 A 的 LU 分 解，即：将矩阵 A 分解为矩阵 L 与上三角矩阵 U，介绍这种运算的普遍规律。
最后再一次提起了之前介绍过的“行交换矩阵”，引入置换矩阵概念。

二、逆矩阵性质补充

看起来就像是沿着左上角开始的一条对角线翻折了一样。

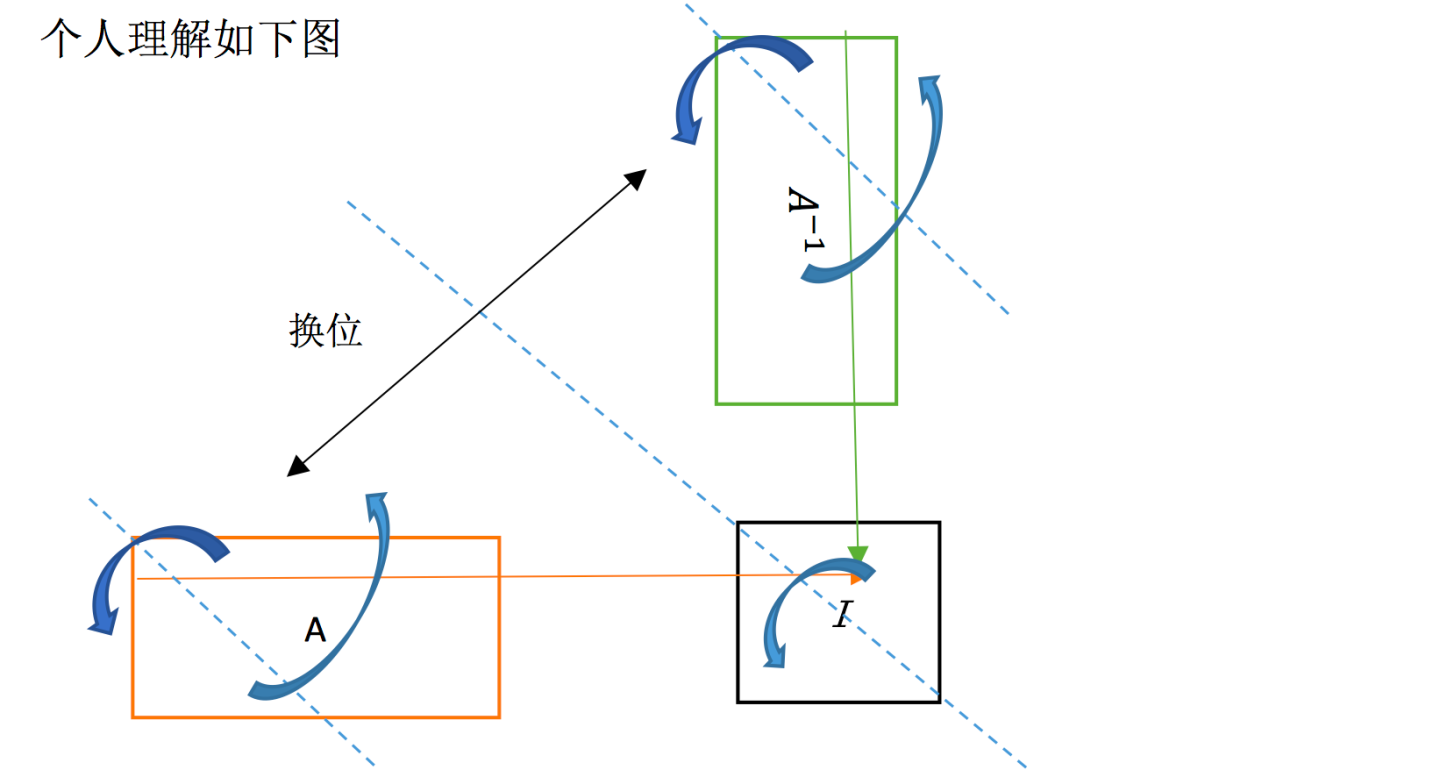
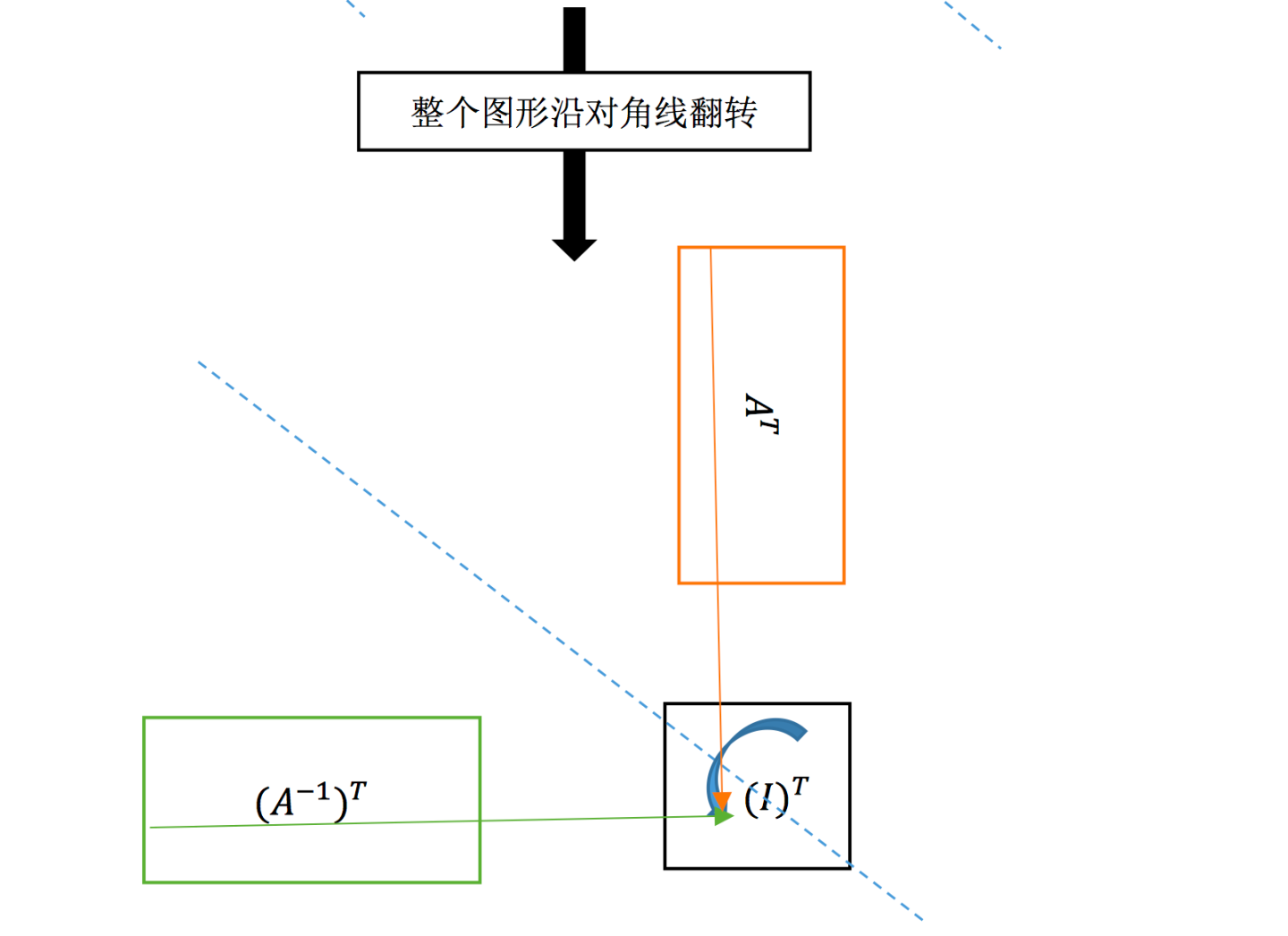
三、A 的 LU 分解

这就给了我们启示，在使用 A = LU 分解矩阵的时候，我们只需要从 U 入 手，反过来考虑，看如何通过行变换可以将上三角矩阵 U 变为 A，然后再将单 位阵按此形式变化，就得到了 L 矩阵。这个性质也是 A = LU 形式分解矩阵的 最大优点，我们甚至不需要知道类似的值到底是什么，我们只需要知道变换形式， 即可求出 L，写出 A = LU 等式。
以上，我们已经学会了 A = LU 分解矩阵方法，那么现在有一个额外问题，就 是消元的运算量问题，比如现在我们有一个 100*100 的超级大的矩阵(无 0 元素）。
我们需要运算（将一行乘一定倍数后加到另一行上消元，每一个这样的过程计为 一次运算）多少次之后，才能将其化为上三角矩阵 U 呢？

四、置换矩阵

我们之前接触过行变换所用到的矩阵，即是将单位阵 I 按照对应行变换方式进 行操作之后得到的矩阵。它可以交换矩阵中的两行，代替矩阵行变换。什么时候 我们需要使用矩阵行变换呢？一个经典的例子就是：在消元过程中，当矩阵主元 位置上面不是 1 时，我们就需要用行变换将主元位置换回 1。
这样的由单位阵变换而来的矩阵，通过矩阵乘法可以使被乘矩阵行交换。我们 将这样的矩阵称为置换矩阵 P。我们通过一个例子来熟悉一下置换矩阵。

注：
推广到 n 阶矩阵，n 阶矩阵有 n！个置换矩阵，就是将单位矩阵 I 各行重 新排列后所有可能的情况数量。我自己的理解是：单看第一行，有 n 种排列方式， 再看除去第一行，第一列的(n-1)阶矩阵，再看其第一行，有(n-1)种排列方式。 以此类推，直到最后的 1 阶，有 1 种排列方式，由乘法原理，就有了 n!个置换 矩阵。