一、知识概要

之前消元处理矩阵时，经常发现矩阵中有时会有一行或几行本身就是前面几 行的线性组合情况，这一节我们就从这种线性相关或线性无关的特征入手，介绍 空间中的几个重要的概念：基，维数。

二、线性无关与线性相关

2.1 背景知识
首先强调，接下来我们谈论的概念都是基于向量组的，而不是基于矩阵。线 性无关，线性相关是向量组内的关系，基也是一个向量组，不要与矩阵概念混淆。
首先从之前学习的 Ax = 0 方程谈起。
假设 mn 的矩阵 A：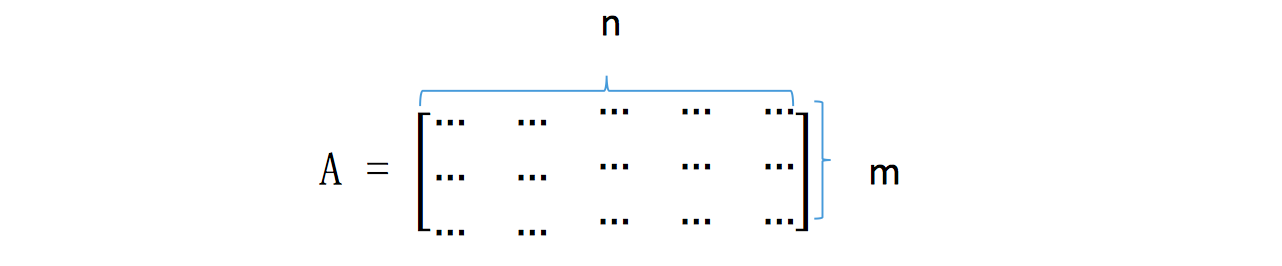
image.png
显然，n > m，以这样的矩阵 A 构成的方程 Ax = 0，此时未知数? ? 的个数比 方程的个数多。未知数一共 n 个，方程一共 m 个。
所以此时 A 的零空间中除零向量以外还有其他向量，原因是这样的 A 一定有 自由变量(至少有 n-m 个自由变量)，这就造成了零空间中向量的无穷解。
2.2 线性无关与线性相关
image.png
image.png
举几个例子感受一下上面的概念：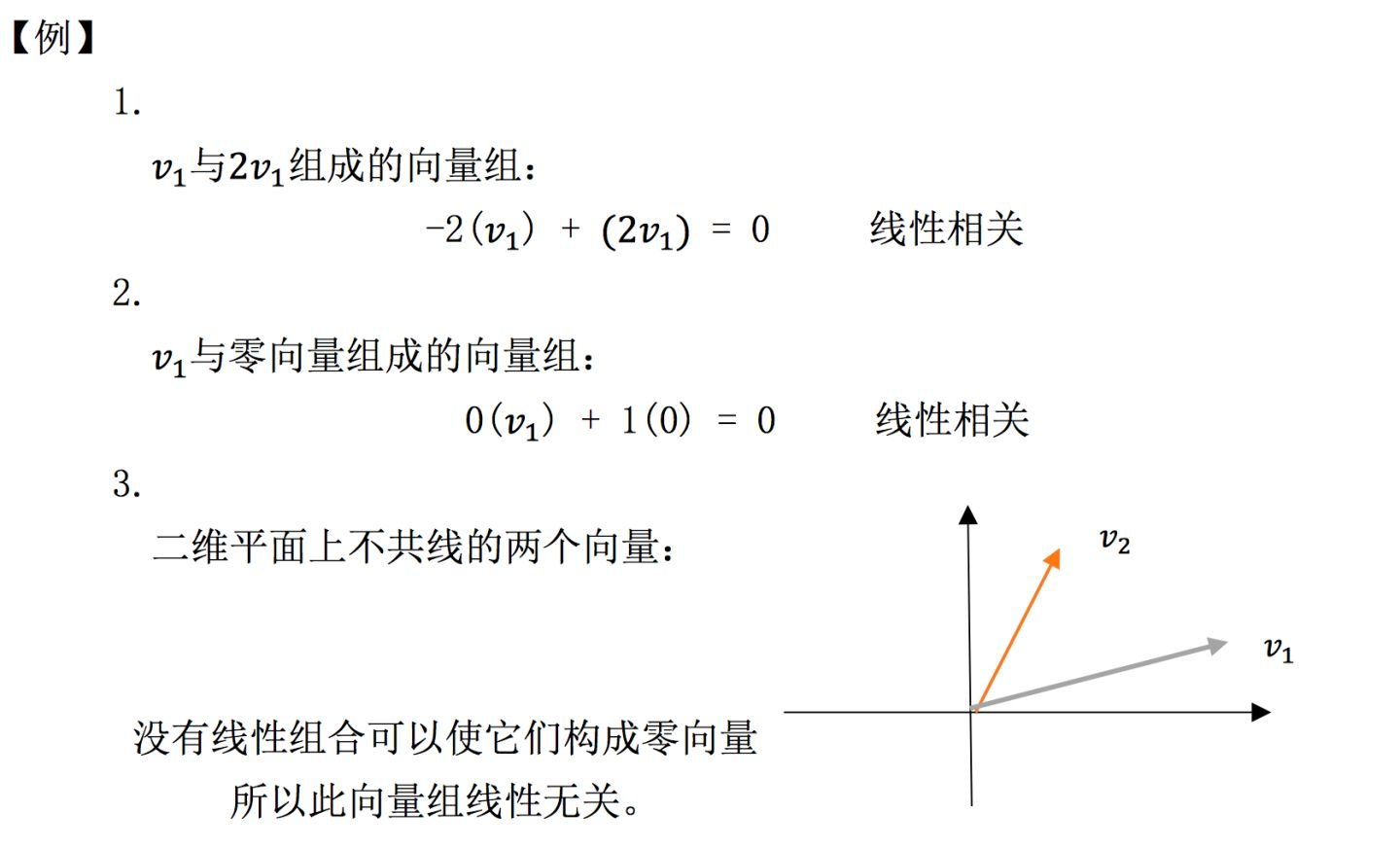
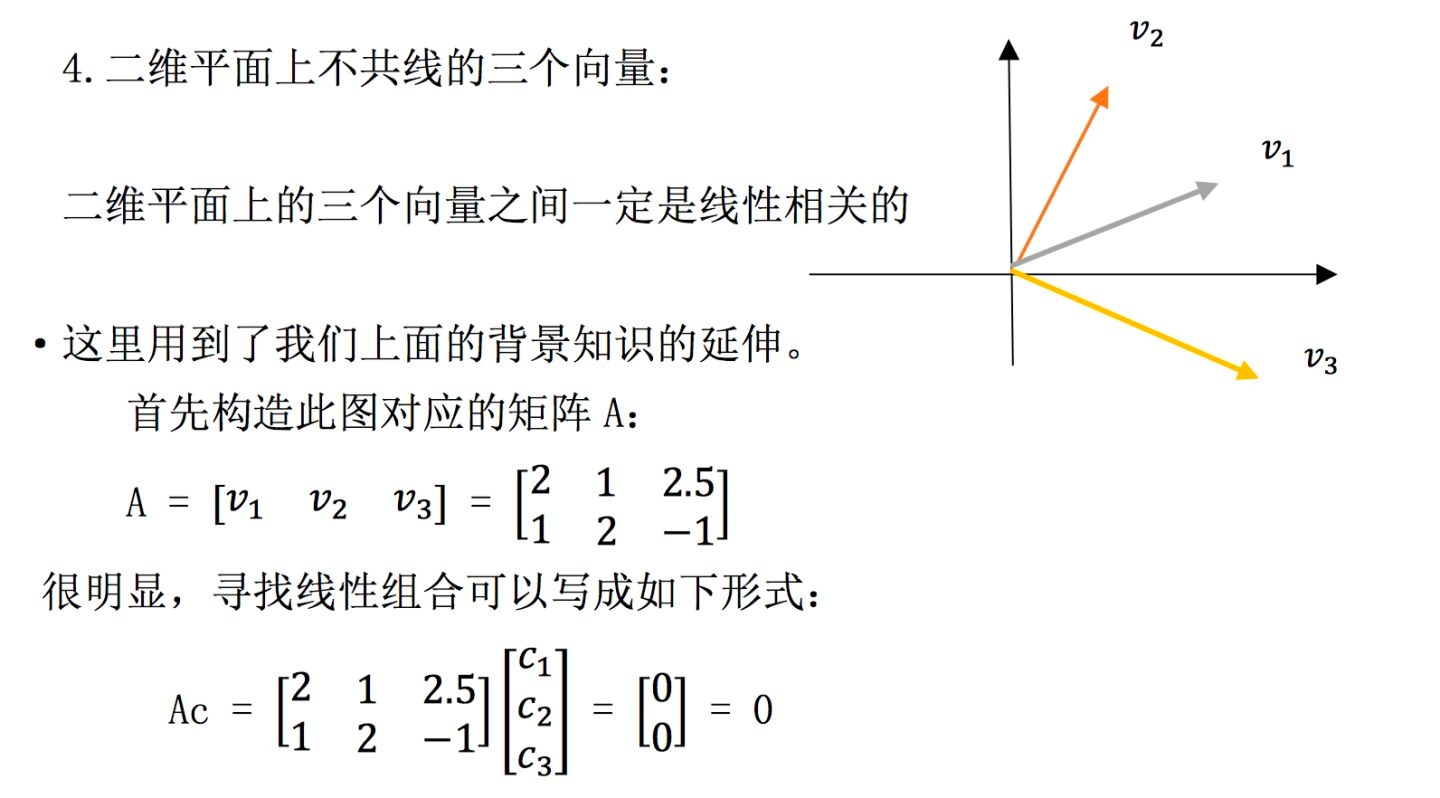
image.png
image.png
image.png
2.3 零空间的作用
根据上面的例题 4，我们再从矩阵的零空间与矩阵列向量角度重新定义 向量组的线性相关/无关。假设现有一 mn 矩阵 A：
·如果 A 各列向量构成的向量组是线性无关的，那么矩阵 A 的零空间中只有零 向量。
·如果 A 各列向量构成的向量组是线性相关的，那么矩阵 A 零空间中除零向 量之外还一定有其他向量。
很好理解上面零空间角度的定义。因为零空间反映的就是 A 各列向量的线性 组合。

从秩的角度看来：
·线性无关对应向量组构成的矩阵，秩为 n，此时没有自由变量，零空间中 只有零向量存在。
·线性相关对应向量组构成的矩阵，秩小于 n，有 n-r 个自由变量，零空间 中有很多向量。
2.4 生成空间
image.png

三、基

image.png
image.png
image.png

四.维数

上面介绍基的时候提到了“? ? 空间的基中向量个数为 n 个。”这个“n”我 们称之为维数。同一个空间内，即使基不同，基向量的个数也必须相等。
理解维数也很简单，像我们的三维空间，其基一定是三个三维向量（三个 向量，每个向量有三个分量），四维空间的基也一定是四个四维向量。

五.总结

这一节学习了很多概念问题，我们通过一道例题回顾一下
image.png
（2）找出A列空间的一个基
从 A 的结构看来：
image.png
这下我们就将矩阵的秩与列空间的维数联系了起来，而更重要的是，我们知 道了列空间的维数，那么在这个列空间中随便找两个线性无关的向量，它们就可 以构成一组基，这组基就可以生成这个列空间。
（3)A对应零空间的维数为多少？
image.png