第十章 偏微分方程数值解法
§3 抛物型方程的差分解法
抛物方程的最简单的是一维热传导方程：
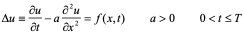（10.35）
它的定解条件主要有以下两类：
（ⅰ）初值问题：（或称柯西Caucy问题）
(10.36)
（ⅱ）边值问题（或称混合问题）
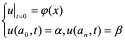（10.37）
求（10.35）满足（ⅰ）或（ⅱ）的解.
（1） 矩形网格
用两组平行直线族x = jh，t = kt (j = 0, ±1, …, k = 0, ±1, …)构成的矩形网覆盖了整个x t平面，网格点（x, t）称为节点，简记为（j, k），h、t 为常数，分别称为空间长及时间步长，（或h称沿x方向的步长，t 称为沿t方向的步长）。
在t = 0上的节点称为边界节点，其余所有属于{-¥<_x_ <+¥, 0< _t __£ T_} 内的节点称为**内部节点**。
（2）古典差分格式：
于平面区域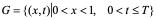
上考虑热传导方程
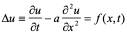
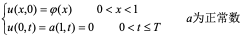
于节点（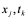
）处微商与差商之间有如下近似关系：
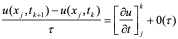
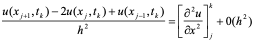
利用上述表达式得到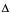
u在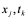（）处的关系式
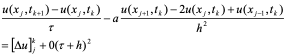（10.38）
当u满足方程式（10.35）时，由（10.38）看出（10.35）在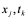（）点可以用下列方程近似地代替：
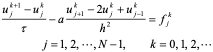（10.39）
式中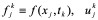
视为
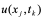的近似值。
差分方程（10.39）称为解热传导方程（10.35）的古典显格式，它所用到的节点图式如下图：
 |
|||||
|
|
|
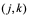
图 10.5
将（10.39）写成便于计算的形式
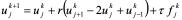（10.40）
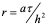称为网比，利用（10.40）及初边值条件（10.37），在网格上的值
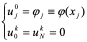（10.41）
即可依次算出k = 1, 2, …，各层上的值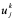
。
从（10.38）若u (x, t)为方程式（10.35）的解，则差分方程（10.39）的截断误差阶为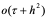
。这个误差的大小将直接影响差分方程解的误差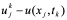
为了提高截断误差的阶，可以得用中心差商：
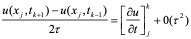
仿古典显格式的讨论，得到如下差分格式：
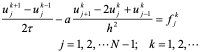（10.42）
它称为Richardson格式，其节点图为：
|
|||||
|
|
|
<br />
图 10.6
截断误差阶为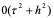
，较古典显格式高。
将（10.42）式改写成适于计算的形式：
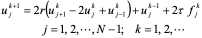(10.43)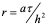为网比，由于在（10.43）中出现了三层网格上的值，故需要先求得第一层网格上的值
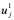，才能逐层计算。
如果利用向后差商
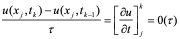
则导出另一差分格式
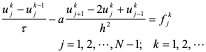(10.44)
或者
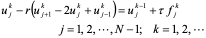（10.45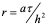）它称为古典隐格式，其节点图为：
|
|
|
|||
|
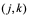
图 10.7
截断误差阶为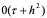
，与古典显格式相同。
我们已经构造出三种差分格式，还可以造出其它格式，它们从形式上看都是可以计算的。那么，这些格式是否可用？哪一种格式更好些？为此必须回答下述问题：
（ⅰ）当步长无限缩小时，差分方程的解是否逼近于微分方程的解？
（ⅱ）计算过程中产生的误差，在以后的计算中是无限增加？还是可以控制？(稳定性)
在适当条件下，从稳定性可以推出收敛性，因此，稳定性问题是研究抛物型差分方程的一个中心课题。
作为例子，现在考查Richardson格式的稳定性。
用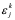
表示计算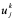所产生的误差，如果右端
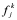无误差存在，则
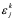满足
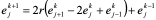取r = 1/2，则
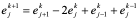（10.46）
假设k – 1层之前无误差存在，即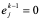
，而在第k层产生了误差，
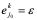，这一层其它点也无误差，而且在计算过程中不再产生新的误差，利用（10.46）式算出误差e 的传播如下表：
表10.5 r = 1/2 时，Richardson格式的误差传播
| J k |
_J_0 - 4 | _J_0 - 3 | _J_0 - 2 | _J_0 - 1 | _J_0 | _J_0 + 1 | _J_0 + 2 | _J_0 + 3 | _J_0 + 4 |
|---|---|---|---|---|---|---|---|---|---|
| k | e | ||||||||
| k + 1 | e | -2e | e | ||||||
| k + 2 | e | -4e | 7e | -4e | e | ||||
| k + 3 | e | -6e | 17e | -24e | 17e | -6e | e | ||
| k + 4 | e | -8e | 31e | -68e | 89e | -68e | 31e | -8e | e |
| k + 5 | -10e | 49e | -144e | 273e | -388e | 273e | -144e | 49e | -10e |
| k + 6 | 71e | -260e | 641e | -1096e | 1311e | -1096e | 641e | -260e | 71e |
<br />从表中看出，误差在迅速增加，因此，这种差分格式是不能使用的。<br /> 如果选用_r_ = 1/2时的古典显格式，此时误差方程为：<br /> 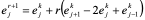<br /> _r_ = 1/2时 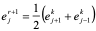 （10.47）<br />此时，误差将逐渐衰减，计算结果列入表10.6。
| J k |
_J_0 - 4 | _J_0 - 3 | _J_0 - 2 | _J_0 - 1 | _J_0 | _J_0 + 1 | _J_0 + 2 | _J_0 + 3 | _J_0 + 4 |
|---|---|---|---|---|---|---|---|---|---|
| k | e | ||||||||
| k + 1 | 0.5e | 0 | 0.5e | ||||||
| k + 2 | 0.25e | 0 | 0.5e | 0 | 0.25e | ||||
| k + 3 | 0.125e | 0 | 0.375e | 0 | 0.375e | 0 | 0.125e | ||
| k + 4 | 0.0625e | 0 | 0.25e | 0 | 0.375e | 0e | 0.25e | 0 | 0.0625e |
对于古典显格式，若选用r = 1，则误差方程为
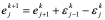
误差传播图如表10.7：
| J k |
_J_0 - 5 | _J_0 - 4 | _J_0 - 3 | _J_0 - 2 | _J_0 - 1 | _J_0 | _J_0 + 1 | _J_0 + 2 | _J_0 + 3 | _J_0 + 4 | _J_0 + 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| k | e | ||||||||||
| k + 1 | e | -e | e | ||||||||
| k + 2 | e | -e | 3e | -2e | e | ||||||
| k + 3 | e | -3e | 6e | -7e | 6e | -3e | e | ||||
| k + 4 | e | -4e | 10e | -16e | 19e | -16e | 10e | -4e | e | ||
| k + 5 | e | -5e | 15e | -30e | 45e | -51e | 45e | -30e | 15e | -5e | e |
经过分析看出，稳定性问题不仅与差分格式有关，而且还与网比有关。如果适当地选取时间步长和空间步长，才能使格式稳定，这种格式的稳定是有条件的，此种稳定称为条件稳定；若格式对任何步长之比都稳定，此种稳定称为无条件稳定或绝对稳定；若格式对任何网比都不稳定，就称为完全不稳定或绝对不稳定。<br /> **稳定性的概念：**差分格式关于初始值稳定的实际含义是，如果其解在某一层存在误差，则由它引起的以后各层上的误差不超过原始误差的M倍，（M为与t无关的长数），因此，只要初始误差足够小，以后各层的误差也足够小。<br /> 下面我们给出一个讨论稳定性的常用富里埃（Fourier）方法，简称富氏方法，我们首先以（10.40）为例，说明富氏方法分析稳定的过程和方法，与（10.40）为相应的误差方程为：<br /> 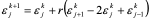 (10.48) <br /> 我们把初始误差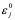表示成一个简谐波的形式：<br /> 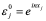 （10.49）<br />式中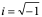，_n_是频率参数，试定形如<br /> 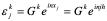 （10.50）<br />的解，这实际上是假定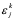的振幅为_G _，频率为_n_的谐波。<br /> 将（10.50）代入（10.48）得<br /> 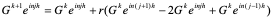<br />两边消去共同因子_G e_ 得<br /> 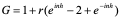 （10.51）<br />这是因为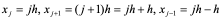。（10.51）是差分方程（10.40）的特征方程，从（10.51）容易容易出<br /> 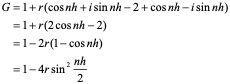 （10.52）<br />这里_G_叫做增长因子（或叫做传播因子），因为从（10.50）可以看到，当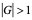时，误差随着_k_作指数增长，当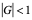时，则误差不增长。由于初始误差可以表为不同频率的谐波的迭加，并且由于计算中舍入误差的随机性，应该认为所有_n_的频率组成部分都是可能出现的，因此数值稳定条件是：<br /> 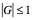，对一切_n_ (10.53)<br /> 从(10.52)看，要<br /> 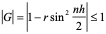<br /> 对一切_n_都成立，必要充分条件是<br /> 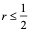或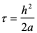 （10.54）<br /> 这说明（10.40）是条件稳定的，当时间步长_t_和空间步长_h_满足不不式（10.54）时为稳定，否则不稳定。<br /> 从上面的讨论过程可以看出，用富氏方法讨论稳定性有这样几个主要步骤：（1）首先假定误差是具有谐波形式的；（2）然后代入差分方程的相应误差方程，得到相应的特征方程；（3）第三是求出特征方程的增长因子；（4）最后判定增长因子是否小于等于1，增长因子小于等于1是稳定的，否则是不稳定的，使增长因子小于等于1的条件，就是稳定条件。<br /> 隐格式（10.45）的特征方程是<br /> 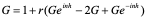<br />这时增长因子为<br /> 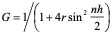 （10.55）<br />无论_t_，_h_如何选取，恒有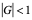，因此格式（10.45）是无条件稳定的，或者称绝对稳定。<br /> 李查逊格式（10.43）的特征方程是<br /> 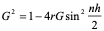<br />_G_有两个根：<br /> 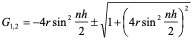 （3.22）<br />不论_t_，_h_怎样选取。总有_n_能使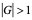，因此李查逊格式是绝对不稳定的，尽管这个格式提高了截断误差阶，但却不能使用。
若有收获，就点个赞吧
0 人点赞
