第十章 偏微分方程数值解法(3)

§4 双曲型方程的差分解法
一阶线性双曲型方程最简单的形式为
(10.4.1)
当给定初始条件
（10.4.2）
以后，容易验证，双曲型方程(10.4.1)的解为：
(10.4.3)
也就是说，在平面 x t上，沿着
（k 是常数）
这样的直线，u的值保持不变。这种直线叫做特征线。
这是个单向的传播波，a>0时，波形j（x）沿x轴方向传播，为右传播波，a < 0时，为左传播波，在传播过程中，波形均不发生变化。
在物理上常见的双曲型偏微分方程最简单模型是波动方程
（10.4.4）
其中，如果引进变量
(10.4.5)
则得到与波动方程等价的方程组
(10.4.6)
可见，二阶双曲型方程可化为一阶双曲型方程组。
下面建立（10.4.1）的差分格式，作网格线


对区域G：进行剖分，其中h = Dx为空间步长，t = Dt为时间步长。
a）迎风格式
u (x, t)用向前差商代替，u（x, t）用向前或向后差商代替，表示u(x, t)近似值，得

或

令l = t / h，得
(10.4.7)
(10.4.8)
截断误差均为，其节点分布见图1。

图1

用Fourier方法讨论（10.4.7）的稳定性：令，代入（10.4.7）得传播因子


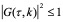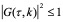当a>0时，恒有，格式（10.4.7）不稳定，当a<0且_al _£ 1时，，格式（10.4.7）稳定。同样可得格式（10.4.8）在_a_ <0时不稳定，在_a_ >0且al £ 1时稳定。称（10.4.7）、（10.4.8）为一阶双曲方程（10.4.1）的逆风差分格式，由于稳定性的要求，a >0时只能用格式（10.4.8），a < 0时只能用式（10.4.7）。为了编制计算程序方便，可将（10.4.7）、（10.4.8）改写为统一形式：
(10.4.9）
稳定性条件为。
b) Lax-Friedrichs格式
(10.4.10）
该格式构造于1954年，用到的技巧，截断误差为，节点分布见图2，传播因子


当时，，即格式（10.4.10）在时稳定。
c）Lax-Wendroff格式
(10.4.11）

图2 图3

该格式构造于1960年，它除使用Taylor级数展开方法外，还反复利用了微分方程本身，其节点分布如图3，截断误差为，传播因子


当时有，即格式（7）在条件下稳定。该格式精度高，节点分布对称，应用上倍受重视。
d）古典隐式格式
前面介绍的均为显式格式，且都是条件稳定格式，计算时，步长的选取受到一定限制，而隐式格式无此限制。
u用向后差商代替，u用中心差商代替得
(10.4.12）
截断误差为，其节点分布见图7.2.4，传播因子


对任意的网格比，均有，故差分格式（10.4.12）是无条件稳定格式。
e）Grank-Nicholson型格式
(10.4.13)
它是在（）处展开，由及中心差商以式而得到的，截断误差为，节点分布见图5，是一个无条件稳定格式。
显式格式计算简便，但都是条件稳定格式，选定空间步长h后，为确保格式的稳定，时间步长的选取要受限制，使之满足稳定性条件，用隐式格式求解时，每计算一个时间层的u值时，需用追赶法求解一个三对角方程组，计算量增大，隐格式是一个无条件稳定格式，从而时间步长t 可选得大些，但也要受计算精度或其它条件的制约。另外，每一个时间层都对应一个方程组，因此隐格式适用于初边值问题和具有周期性条件的初值问题，一般的初值问题不适用。

图4 图5

二、二阶双曲型方程的差分格式
这里将直接构造方程的差分格式
a）显式格式
u, u均用中心差商代替之，得
(10.4.14）
即


图6

其中网格比，截断误差，节点分布见图6，这是三层显示格式，当n ³2时，可用（10.4.14）计算，n = 1时，欲计算需借助于初值条件的离散化，以后再做介绍。三层差分格式须引入新的未知量，化为二层格式后，再用Fourier方法讨论其稳定性，推导从略，这里仅给出差分格式（10.4.14）的稳定性条件：。
b）隐格式
利用关系

可得三层隐式格式：
(10.4.15）
即

截断误差是，节点分布见图7，可证明此格式绝对稳定。已知n层，n－_1层的_u值，由格式（10.4.15），借助追赶法，可求得n + 1层的u值。