计算机图形学 – 常用的3D数学知识备忘，如三角函数、向量运算、矩阵运算、图形学常用的平移缩放旋转矩阵，视图矩阵，投影矩阵

StubbornHuang 3D数学基础 2021-12-17 414 0 2 百度未收录 本文共4032个字，阅读需要11分钟。
本文作者：StubbornHuang
版权声明：本文为站长原创文章，如果转载请注明原文链接！
原文标题：计算机图形学 – 常用的3D数学知识备忘，如三角函数、向量运算、矩阵运算、图形学常用的平移缩放旋转矩阵，视图矩阵，投影矩阵
原文链接：https://www.stubbornhuang.com/1865/
发布于：2021年12月17日 16:29:54
修改于：2021年12月22日 11:30:06

1 三角函数

1.1 圆周率

π≈3.14159265fπ≈3.14159265f
实际上ππ有无穷个小数。

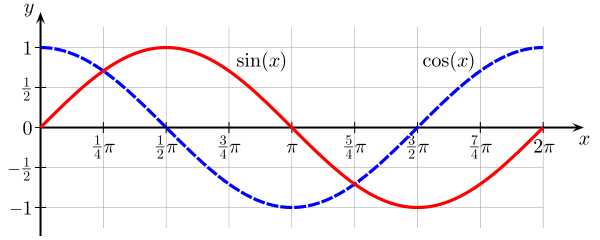
1.2 余弦与正弦

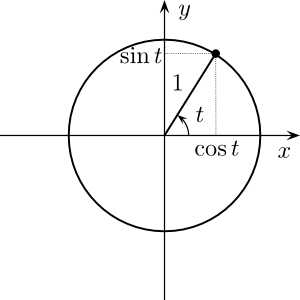
1.3 单位圆

t 是以弧度为单位的角度。

1.4 弧度与角度的转换

角度转弧度：
angleRad=angleDeg∗Math.PI/180;angleRad=angleDeg∗Math.PI/180;
弧度转角度：
angleDeg=angleRad∗180/Math.PI;angleDeg=angleRad∗180/Math.PI;

2 向量

2.1 向量加法

两个向量的和组成一个三角形。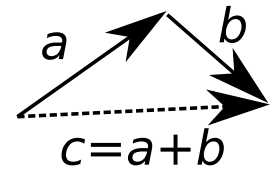

同时：
a=c−bb=c−aa=c−bb=c−a

2.2 单位向量 - 归一化向量

单位向量用于表示方向或者法向，长度为1。
A^=A⃗∥A⃗∥A^=∥∥∥∥A∥∥∥∥A
其中 ∣A⃗∣∣∣∣∣A∣∣∣∣ 是 A^A^ 的长度。

2.3 向量点乘

向量点乘可用于获取两个向量之间的夹角。
A⃗⋅B⃗=∑i=1nAiBi=A1B1+A2B2+⋯+AnBnA⋅B=i=1∑nAiBi=A_1_B_1+_A_2_B_2+⋯+_AnBn
向量点乘的结果为标量值。
那么两个向量的夹角等于：
θ=arccos⁡(A^⋅B^)θ=arccos⁡(A^⋅B^∥A^∥∥B^∥)θ=arccos(A^⋅B^)θ=arccos(∥∥∥∥A^∥∥∥∥∥∥∥∥B^∥∥∥∥A^⋅B^)
当两个向量之间的夹角为90度时，这两个向量的点积为0；当两个向量的夹角为0度时，这两个向量的点积为1。

2.4 向量叉乘

向量叉乘生成一个垂直于向量A和向量B共有平面的新向量。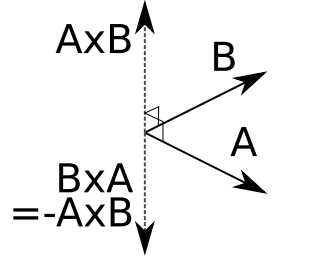

向量叉乘形式如下：
[a1a2a3]×[b1b2b3]=[a2b3−a3b2a3b1−a1b3a1b2−a2b1]⎣⎢⎡a_1_a_2_a_3⎦⎥⎤×⎣⎢⎡_b_1_b_2_b_3⎦⎥⎤=⎣⎢⎡_a_2_b_3−_a_3_b_2_a_3_b_1−_a_1_b_3_a_1_b_2−_a_2_b_1⎦⎥⎤
向量叉乘可用于计算平面的法向：
N=normalize(cross(A,B))_N=normalize(cross(A,B))

3 矩阵

3.1 单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。
I3=[100010001]I_3=⎣⎢⎡100010001⎦⎥⎤
如果 AB=I_AB=I，那么矩阵 AA 为 矩阵 BB 的逆。

3.2 矩阵与向量相乘

[abcdefghi][xyz]=[ax+by+czdx+ey+fzgx+hy+iz]⎣⎢⎡adgbehcfi⎦⎥⎤⎣⎢⎡xyz⎦⎥⎤=⎣⎢⎡ax+by+czdx+ey+fzgx+hy+iz⎦⎥⎤

3.3 矩阵与矩阵相乘

AB=[abcd][efgh]=[ae+bgaf+bhce+dgcf+dh]AB=[acbd][egfh]=[ae+bgce+dgaf+bhcf+dh]

3.4 矩阵行列式

假如矩阵MM为：
M=[abcdefghi]M=⎣⎢⎡adgbehcfi⎦⎥⎤
则其行列式 ∣M∣∣M∣ 为：
∣M∣=aei+bfg+cdh−ceg−bdi−afh∣M∣=aei+bfg+cdh−ceg−bdi−afh

3.5 矩阵转置

假如矩阵MM为：
M=[abcdefghi]M=⎣⎢⎡adgbehcfi⎦⎥⎤
在上述矩阵在主对角线上翻转矩阵元素得到矩阵的转置。
则其转置矩阵MTMT为：
MT=[adgbehcfi]MT=⎣⎢⎡abcdefghi⎦⎥⎤
当矩阵为正交矩阵时，矩阵的转置矩阵就为矩阵的逆。

3.6 矩阵的逆

通常使用逆矩阵翻转矩阵变换或者相对于另一个对象进行变换。
MM−1=IMM−1=I
其中II为单位矩阵，M−1M−1为逆矩阵。
如果矩阵的行列式为 0，则没有逆矩阵。

4 齐次矩阵

4.1 行主序齐次矩阵

行主序齐次矩阵在Direct3D中使用，
v′=[VxVyVz1][XxXyXz0YxYyYz0ZxZyZz0TxTyTz1]v′=[_VxVyVz_1]⎣⎢⎢⎢⎡_XxYxZxTxXyYyZyTyXzYzZzTz_0001⎦⎥⎥⎥⎤

4.2 列主序齐次矩阵

列主序齐次矩阵在OpenGL中使用，
v′=[XxYxZxTxXyYyZyTyXzYzZzTz0001][VxVyVz1]v′=⎣⎢⎢⎢⎡_XxXyXz_0_YxYyYz_0_ZxZyZz_0_TxTyTz_1⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡_VxVyVz_1⎦⎥⎥⎥⎤

4.3 平移、缩放、旋转

列主序下的平移矩阵：
T=[100Tx010Ty001Tz0001]T=⎣⎢⎢⎢⎡100001000010TxTyTz_1⎦⎥⎥⎥⎤
列主序下的缩放矩阵：
S=[Sx0000Sy0000Sz00001]_S=⎣⎢⎢⎢⎡Sx_0000_Sy_0000_Sz_00001⎦⎥⎥⎥⎤
列主序下的旋转矩阵：
Rx=[10000cos⁡(θ)−sin⁡(θ)00sin⁡(θ)cos⁡(θ)00001]_Rx=⎣⎢⎢⎢⎡10000cos(θ)sin(θ)00−sin(θ)cos(θ)00001⎦⎥⎥⎥⎤
Ry=[cos⁡(θ)0sin⁡(θ)00100−sin⁡(θ)0cos⁡(θ)00001]Ry=⎣⎢⎢⎢⎡cos(θ)0−sin(θ)00100sin(θ)0cos(θ)00001⎦⎥⎥⎥⎤
Rz=[cos⁡(θ)−sin⁡(θ)00sin⁡(θ)cos⁡(θ)0000100001]Rz=⎣⎢⎢⎢⎡cos(θ)sin(θ)00−sin(θ)cos(θ)0000100001⎦⎥⎥⎥⎤

4.4 视图矩阵

列主序下的视图矩阵，
V=[RxRyRz−PxUxUyUz−Py−Fx−Fy−Fz−Pz0001]V=⎣⎢⎢⎢⎡RxUx−Fx_0_RyUy−Fy_0_RzUz−Fz_0−_Px−Py−Pz_1⎦⎥⎥⎥⎤
其中U_U为视点的向上向量，FF为视点的向前向量，PP为摄像机的世界坐标。
鸟瞰图的视图矩阵为:
V=[100000−1001000001]V=⎣⎢⎢⎢⎡100000100−1000001⎦⎥⎥⎥⎤

4.5 投影矩阵

列主序下的投影矩阵，
P=[Sx0000Sy0000SzPz00−10]P=⎣⎢⎢⎢⎡Sx_0000_Sy_0000_Sz−100Pz_0⎦⎥⎥⎥⎤
其中：
Sx=(2∗ near )/( range ∗ aspect + range ∗ aspect )Sy= near/range Sz=−( far + near )/( far − near )Pz=−(2∗ far ∗ near )/( far − near ) range =tan⁡( fov /2)∗ near _Sx=(2∗ near )/( range ∗ aspect + range ∗ aspect )Sy= near/range Sz=−( far + near )/( far − near )Pz=−(2∗ far ∗ near )/( far − near ) range =tan( fov /2)∗ near

4.6 常用的矩阵变换

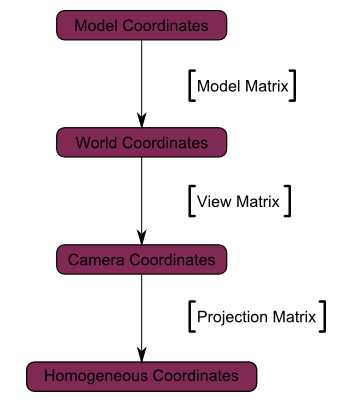
Model Matrix：模型矩阵，即4.3节中所述的平移、缩放、旋转变换；
View Matrix：视图矩阵，即4.4节中所述的视图矩阵；
Projection Matrix：投影矩阵，即4.5节中所述的投影矩阵；
模型坐标通过模型矩阵（即平移、缩放、旋转变换）转化为世界空间坐标，再通过视图矩阵变为相机坐标，最后通过投影矩阵变为齐次坐标。

参考链接

1. https://antongerdelan.net/teaching/3dprog1/maths_cheat_sheet.pdf
2. http://www.opengl-tutorial.org/miscellaneous/math-cheatsheet/
3. https://gist.github.com/xem/99930986c5333125a13b0ea50600391f

4