第一章:求极限

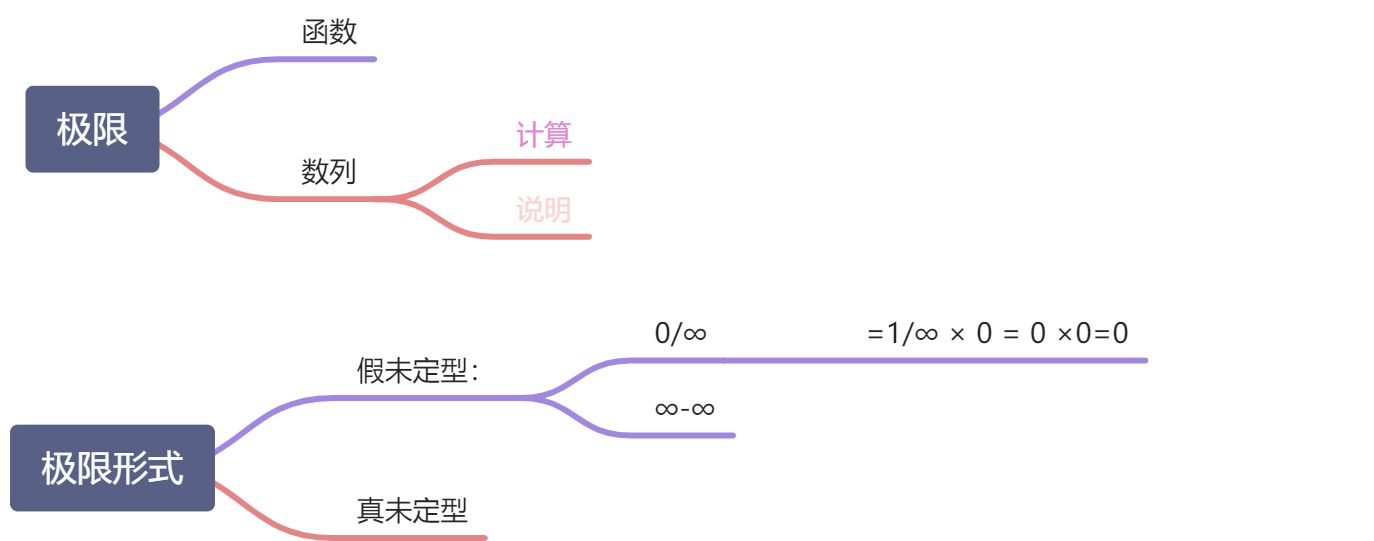
第一章:求极限

一、极限：

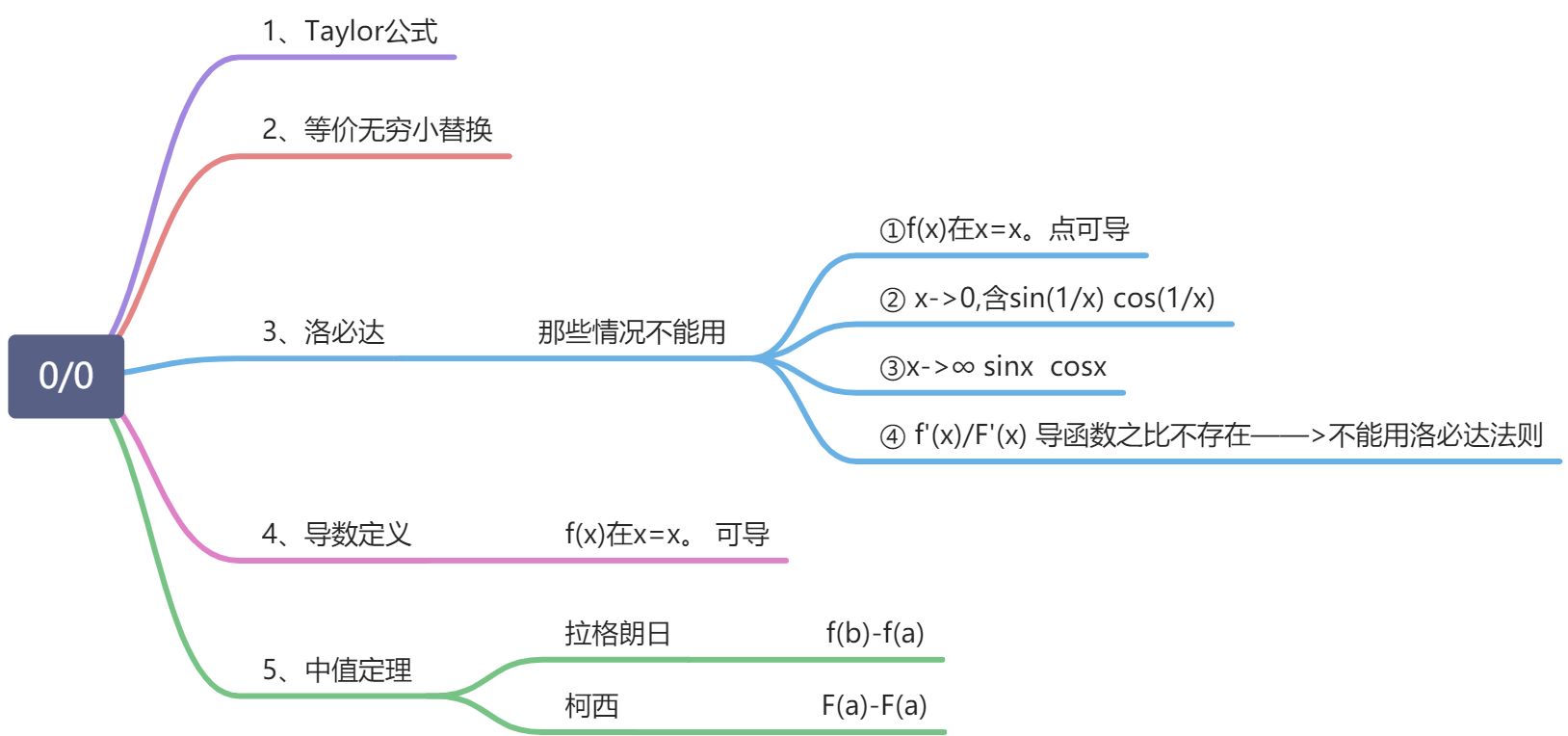
专题 七种未定型求极限

无穷小阶的判定 ：间断点 、渐近线

已知极限

无穷小量

若

无穷小的比较：

若

• (1) 高阶 ：若 记为g(x)=o(g(x));

(2) 同阶 ：若 ;

(3) 等价：若 ；记为f(x)~g(x);

一、常见的求极限的方法

1.四则运算：分母不为零的

二、运用泰勒公式进行极限运算

（1）泰勒公式为：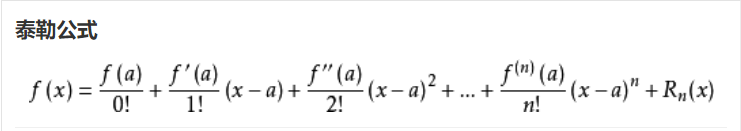

在 x——>0的速度快慢的比较来反映麦克劳林公式：
对于 X3 X5
X3=o(x)
X5 =o(x2)
o(x) +o(x2)=o(x)

由泰勒公式推出8个常用的麦克劳林公式:

再由这8个麦克劳林公式进而演变成等价无穷小替换的形式;

=
=-2

===>等价无穷小替换是泰勒公式的特殊性

注意：
泰勒公式是求解0/0型极限的一个极为有效的方法在应用过程中，一定要保证展开的变量趋近于零；

展开原则：
（1）复杂函数展开后系数相抵消到不为零的那一阶，低阶加高阶等价于低阶，故有一低阶存在（假设为x的k阶无穷小），其他高阶项都可以用o(xk)来表示
（2）展开分子分母同阶：
f(x)+-g(x) 抵消不了（展开）
例：

符合 f(x)+-g(x) 抵消不了
解：因为： 3sinx=3x-3/6x3+o(x3)
sin3x=3x-1/6(3x)3+o(x3)