背景:
FFM是Yuchi Juan 在2016年提出,受Rendle在2010年发表的PITF模型的启发。FFM可以看做是FM的升级版(FM也是2010年发表)
分析:
1、FFM介绍
相对于FM模型,FFM模型引入了域(Field)的概念,可以看做是对特征的分组。比如,对于性别特征来说,一般有两种取值男人、女人。对特征进行one-hot编码后性别特征会拆分成两个独立的特征和
。显然,这两个特征具有共同的性质:都想属于性别。所以可以把这两个特征归到同一个Field下。即有相同的Field编号。不同Field之间的特征,往往具有明显的差异性。对比FM中的做法,每个特惠只能对应一个隐向量,在对某个特征
与其他特征交叉时,始终使用同一个隐向量
。这种无差别的交叉方式,并没有考虑到不同特征之间的共性(同域)与差异性(异域)。
FFM公式如下:
其中为域(Field)映射函数,
表示为
特征对应的FIeld编号。
FM公式:
对比FM,两者之间的差异仅仅是二阶交叉的隐向量不同。假设数据集中有个特征,这些特征的Field的数量为F,那么对应每个特征
都有F个隐向量,分别用于与不同FIeld域特征进行交叉,假设隐向量的维度是k,那么FFM的二阶交叉项参数为
。
求解
由于引入了FIeld,公式(1)不能像FM那样进行公式改写,所以FFM模型进行推断时的时间复杂度为
为方便推导各参数的梯度,隐向量表示为。公式展开后:
优缺点:
优点:
- 在高维稀疏的数据集中表现很好
-
缺点:
时间开销大。FFM的时间复杂度为
,FM的时间复杂度为
参数多,容易过拟合,需加入正则化,以及早停的训练策略注意事项:
FFM对数据集的要求:
- 含有类别特征的数据集,且需要对特征进行二值化处理
- 越是稀疏的数据集表现效果优于其他模型
- 比较难处理纯数值类型的数据
- 超参对模型的影响:
隐向量维度对模型的影响不大,需要注意的是FFM的隐向量维度远小于FM隐向量的维度,即

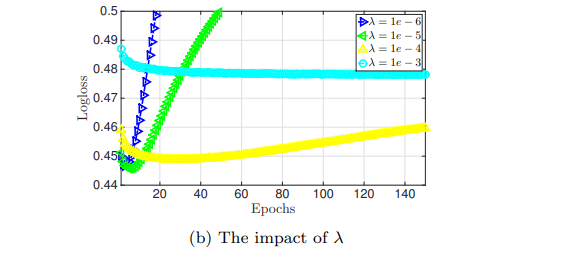
正则化系数
如果太大,容易导致欠拟合,反之,容易过拟合
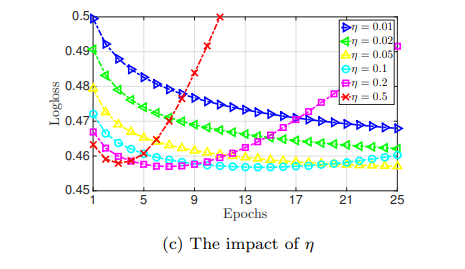
在论文中,使用的是Adagrad优化器,全局学习率
也是超参数。如果
在一个较小的水平,则可以表现最佳。多大,容易导致过拟合,过小,容易导致欠拟合。
#-*- coding:utf-8 -*-
# @Time:2020/11/6 11:25
# @Auther :lizhe
# @File:FFM.py
# @Email:bylz0213@gmail.com
import tensorflow.compat.v1 as tf1
class FFM:
def __init__(self,fea_num,hidden_num,n_field):
self.fea_num = fea_num
self.hidden_num = hidden_num
self.lamda = 1e-4
with tf1.variable_scope('input'):
self.x = tf1.placeholder(dtype=tf1.float32, shape=[None,self.fea_num], name='input_x')
self.y = tf1.placeholder(dtype=tf1.float32, shape=[None,1], name='input_y')
with tf1.variable_scope('wegiht'):
self.w_bais = tf1.get_variable(dtype=tf1.float32, shape=[1], name='weight_bais')
self.w_linear = tf1.get_variable(dtype=tf1.float32, shape=[fea_num], name='weight_linear')
self.w_h = tf1.get_variable(dtype=tf1.float32, shape=[fea_num,n_field,hidden_num] ,name='weight_hidden')
self.rr = 0
linear = tf1.multiply(self.x, self.w_linear) + self.w_bais
field_map = lambda x: 0 if x%2 ==0 else 1
for i in range(self.fea_num):
for j in range(i+1,self.fea_num):
self.rr += tf1.reduce_sum(tf1.multiply(self.w_h[i,field_map(j)],self.w_h[j,field_map(i)]))*tf1.multiply(self.x[:, i], self.x[:, j])
y_hat = linear + self.rr
self.loss_ = tf1.reduce_mean(tf1.square(self.y - y_hat))
self.reg_loss = self.lamda * (tf1.reduce_mean(tf1.nn.l2_loss(self.w_linear)) + tf1.reduce_mean(tf1.nn.l2_loss(self.w_h)))
self.loss = self.loss_ + self.reg_loss

