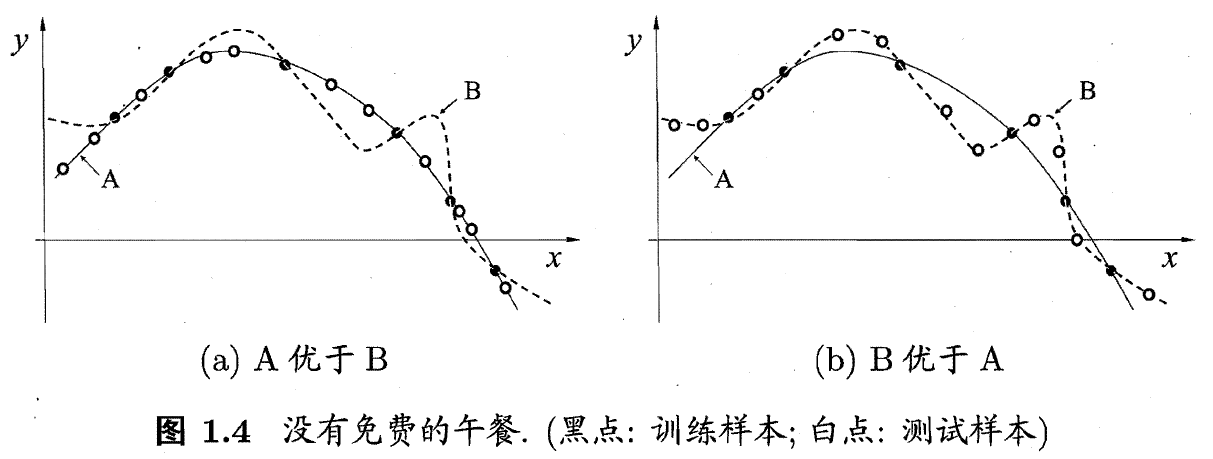
没有免费的午餐 (No Free Lunch Theorem, NFL)

没有免费午餐定理（No Free Lunch Theorem, NFL）是由 Wolpert 和 Macerday 在最优化理论中提出的。

白话定理

对于基于迭代的最优化算法不会存在某种算法对所有问题（有限的搜索空间内）都有效。如果一个算法对某些问题有效，那么它一定在另一些问题上比纯随机搜索算法更差。也就是说，不能脱离具体问题来讨论算法的优劣，任何算法都有优劣性，必须要「具体问题具体分析」。
平常所说的一个学习算法比另一个算法更「优越」，效果更好，只是针对特定的问题、特定的先验信息、数据的分布、训练样本的数目、代价或奖励函数等。
NFL 定理说明了无法保证一个机器学习算法在 以外的数据集上一定能分类或预测正确，除非加上一些假设条件。

数学描述

定理证明

假设样本空间 和假设空间 都是离散的，令 代表算法 基于训练数据 产生假设 的概率，再令 代表希望学习的真实目标函数。 的「训练集外误差」，即 在训练集之外的所有样本上的误差为：

其中， 是指示函数，若 为真则取值 1，否则取值 0。

考虑二分类问题，且真实目标函数可以是任何函数 ，函数空间为 。对于所有可能的 按均匀分布对误差求和，有：

该式表明，无论学习算法 多聪明、学习算法 多笨拙，它们的期望性能尽然相同。

该证明的解释：
：样本空间；
：假设空间；
：训练数据（即样本内数据）；
：未知数据（即样本外数据）；
：假设；
：算法；
：希望学习的真实目标函数；
ote：off-training error，即训练集外误差；

：算法 学得的假设在训练集外的所有样本上的误差的期望；

：样本空间中的每个样本 取得的概率；

：假设 对一个样本点 的预测误差，预测值 与真实值 一致则误差为 0，不一致则误差为 1；

：对于样本空间中每一个训练集外的数据都进行右边的运算并加总求和；

：假设函数 在训练集之外的所有样本上的误差

：算法 基于训练数据 产生假设 的概率；

：对于所有假设都进行右边的运算并加总求和；

： 是算法 以概率 产生的，该式定义算法 的误差为所有可能的 的误差的期望；

：整个函数空间的大小。二分类问题中假设真实目标函数 可以是任何输入空间 到输出空间 的映射。

：假设在整个函数空间中所有可能的目标函数 是均匀分布的（即所有真实的问题是均匀出现的），在二分类问题中，对于一个样本点 ，假设函数 的预测值要么是 0 要么是 1，那么由于 是均匀分布的，所有将 映射为 0 的真实函数 的数量和所有将 映射为 1 的真实函数 的数量应该是一样的，那么，在函数空间中就有一半数量的可能的 与假设函数 的预测不一致。

丑小鸭 (Ugly Duckling Theorem)

丑小鸭定理（Ugly Duckling Theorem）是 1969 年由渡边慧提出的 [Watan-able, 1969]。

白话定理

「丑小鸭与白天鹅之间的区别和两只白天鹅之间的区别一样大」。这个定理初看好像不符合常识，但是仔细思考后是非常有道理的。因为世界上不存在相似性的客观标准，一切相似性的标准都是主观的。如果以体型大小的角度来看，丑小鸭和白天鹅的区别大于两只白天鹅的区别；但是如果以基因的角度来看，丑小鸭与它父母的差别要小于他父母和其他白天鹅之间的差别。

定理证明

假设宇宙中有 个事物，并且想要将它们分类。对于什么样的事物属于什么类别没有任何先入为主的观念。因此必须考虑所有可能的分类方式，共有 种。
可以用它来度量两个对象之间的相似性：可以观察它们有多少共同的集合。
但这是不可能的。因为，如果可以形成任何可能的分类，那么任何两个对象都有完全相同数量的分类，即 个类（总数的一半）。
因此，如果我们对于哪些类别更好没有先入为主的偏见，那么所有的东西都是相似的（或都是不相似的）。
该定理启示，做出判断需要某种提前的假设，即需要某种归纳偏置。

奥卡姆剃刀 (Occam’s Razor)

奥卡姆剃刀（Occam’s Razor）是由 14 世界逻辑学家 William of Occam 提出的一个解决问题的法则。

白话定理

「如无必要，勿增实体」。
奥卡姆剃刀的思想和机器学习上的正则化思想十分相似：简单的模型泛化能力更好。如果有两个性能相近的模型，我们更倾向于选择简单的模型。因此在机器学习准则上，我们经常会引入参数正则化来限制模型的能力，避免过拟合。

数学描述

奥卡姆剃刀的一种形式化是最小描述长度（Minimum Description Length, MDL）原则，即对一个数据集 ，最好的模型 是会使得数据集的压缩效果最好，即编码长度最小。
最小描述长度也可以通过贝叶斯学习的观点来解释，模型 在数据集 上的对数后验概率为：

其中， 和 可以分别看作在该模型下数据集 的编码长度和模型 的编码长度和，也就是说我们不但要使得模型 可以编码数据集 ，也要使模型 尽可能的简单。

归纳偏置 (Inductive Bias)

白话定理

在机器学习中，很多算法会对学习的问题做一些假设，这些假设就称为归纳偏置（Inductive Bias）。
归纳偏置所做的事情，是将无限可能的目标函数约束在一个有限的假设类别之中，这样，模型的学习才成为可能。

比如：

• 最近邻分类器中，假设在特征空间内，一个小的局部区域中的大部分样本都属于同一类；
• 朴素贝叶斯分类器中，假设每个特征的条件概率是相互独立的；
• SVM 中，假设好的分类器应该最大化类别边界距离；
• CNN 中，假设特征具有局部性 (Locality)，即当我们把相邻的一些特征放在一起，会更容易得到「解」；
• RNN 中，假设每一时刻的计算依赖于历史计算结果；

归纳 (Induction)：是自然科学中常用的两大方法（归纳与演绎, Induction and Deduction）之一，指的是从一些例子中寻找共性、泛化，形成一个比较通用的规则的过程；
偏置 (Bias)：是指我们对模型的偏好。

归纳偏置可以理解为，从现实生活中观察到的现象中归纳出一定的规则 (Heuristics)，然后对模型做一定的约束，从而可以起到「模型选择」的作用，即从假设空间中选择出更符合现实规则的模型。归纳偏置在贝叶斯学习中也称为先验（Priors）。

计算学习理论

二分类

二分类 (binary classification) 问题是将一组数据按照某个规则分为两类。用 h(x) = 1 和 h(x) = -1 分别表示正例和反例。

正射线 (Positive Ray)

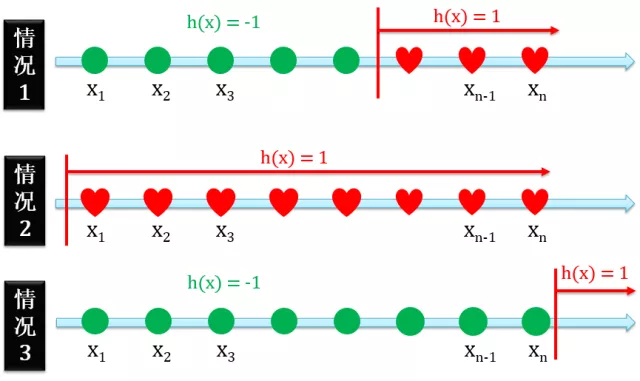
正射线二分类的定义是在某个点的右边全是正例。有三种情况：

1. 正例在反例的右边
   
2. 只有正例没有反例
   
3. 只有反例没有正例
   

正间隔 (Positive Interval)

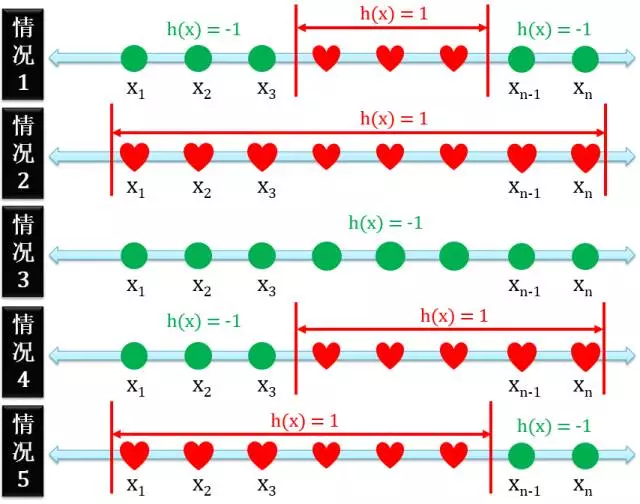
正间隔二分类的定义是在某两个点的中间全是正例，有五种情况：

1. 正例在反例的中间
   
2. 只有正例没有反例
   
3. 只有反例没有正例
   
4. 正例右边没有反例
   
5. 正例左边没有反例
   

一维感知器 (1D Perceptron)

一维感知器就是正射线和负射线的合体，有四种情况：

1. 正例在反例的右边
   
2. 正例在反例的左边
   
3. 只有正例没有反例
   
4. 只有反例没有正例
   

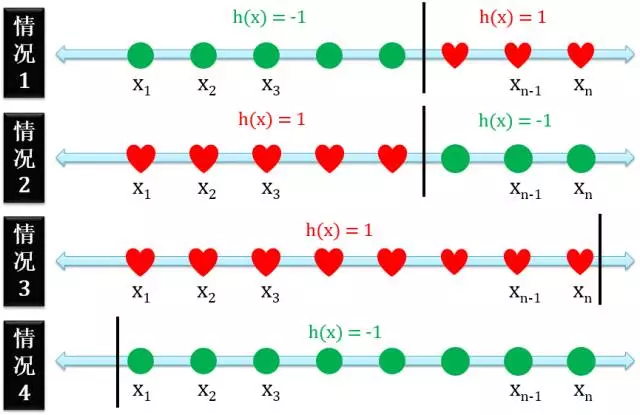
二维感知器 (2D Perceptron)

二维感知器就是一维感知器从线升级到面。

对分 (Dichotomy)

二分类问题中，假设输入空间为 ，假设空间为 ，有限的样本为 ，假设 将 输入空间 映射到 ，假设空间上的对分定义为：

二分类问题中，数据集 里面有 个样例，如果考虑用某种方法给这 个样例赋予 2 个标记的话，有 个结果。假设经过某种操作 是将正类和负类线性分开，这种分开的操作定义为对分 (Dichotomy)，记为 。
对分的结果最多有 个，但是通常会少于甚至远少于 个。

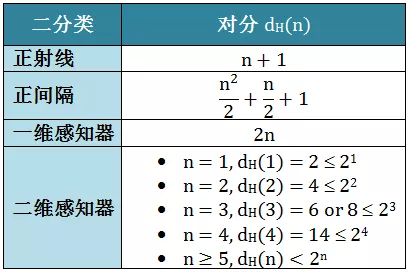
增长函数 (Growth Function)

对分运用起来有一点麻烦，由于对分个数在固定 点的情况下可能有多个值，它不仅和点的个数 有关，还和点的分布情况有关。
增长函数 (Growth Function) 是一个只和 有关的量，它取每个 点对分时的最大值。

增长函数值越大则这个操作 的表示能力越强（我们把这个操作 定义成机器学习的假设空间 ），复杂度也越高，学习任务的适应能力越强。

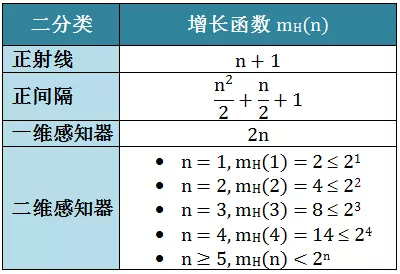
打散 (Shatter)

假设经过某种操作 能实现数据集 上所有的对分，则称数据集 能被这个操作 打散 (Shatter)。
既然能实现所有对分，那么打散时对应的增长函数为 。

突破点 (Break Point)

把第一个没被打散对应的 点称为突破点 (Break Point)。即，满足：

的 的最小值就是突破点。

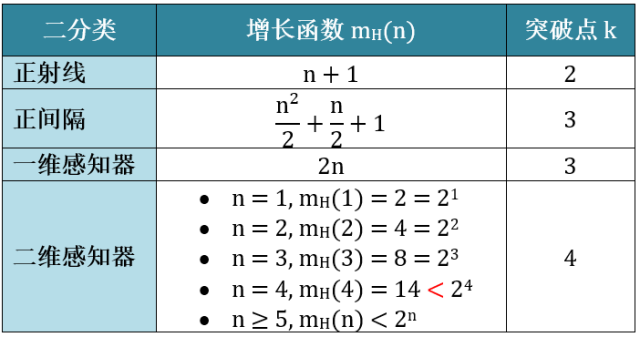
增长函数的上界

表示当突破点为 时，增长函数 可能的最大值，即 是 的上界，对应 最多有多少种对分。

假设 ，对分的情况如下：

观察 ，有些对分在这 个点里只出现了一次（不考虑 ，即 要么为 +1 要么为 -1），将这些对分情况归入 ；有些对分在这 个点里出现了两次（ 分别为 +1 和 -1），将这些对分情况归入 。
中 的部分归入 ； 中 的部分归入 。
假设 有 行， 和 都有 行，因为行的总数限定为 ，于是有：

对于前 个点，因为 和 的前 个点相同，因此它们的对分也一样，于是，前 个点不同的对分总数为：。
因为 个点的任意 个点均不能被打散，所以前 个点的任意 个点均不能被打散，于是：

若 能被 个点打散，而 是成对存在的，则 组成的 必然能被 个点打散，因为 总能取到 +1 或 -1。因此有：

将式 (2) 和 (3) 代入 (1) 中，得到：

使用该式递归得到下表：

上表第一行和第一列通过实际计算得到。

Sauer’s Lemma

定理

证明

当 或 时，上式成立。
假设对于所有的 和所有的 ，上式成立，需证明对于所有的 和所有的 ，上式成立。
因为对于所有的 ， 时上式成立，因此只需考虑 。
因为：

其中用到 。因为从 个物体中选择 个物体的方式，要么第 1 个被选中，于是相当于从剩下的 个物体中选择 个，即 ；要么第 1 个没被选中，于是相当于从生下的 个物体中继续选 个，即 。
根据上式，证得：

定理

若存在 使 ，则对于所有的 ，有：

其中，不等式右边是 的 阶多项式。即：

布尔不等式/联合上界 (Union Bound)

定理

布尔不等式（Boole’s Inequality）也叫（Union Bound），即并集的上界，描述的是至少一个事件发生的概率 #card=math&code=%5Cmathbb%7BP%7D%5Cleft%28%5Cbigcup_i%20A_i%5Cright%29) 不大于单独事件（事件之间未必独立）发生的概率之和 #card=math&code=%5Csum_i%5Cmathbb%20P%28A_i%29)

即：
%5Cleq%20%5Csum_i%5Cmathbb%20P(A_i)%0A#card=math&code=%5Cmathbb%7BP%7D%5Cleft%28%5Cbigcup_i%20A_i%5Cright%29%5Cleq%20%5Csum_i%5Cmathbb%20P%28A_i%29%0A)

展开即为：
%5Cleq%20%5Cmathbb%20P%5Cleft(A_1%5Cright)%2B%5Cmathbb%20P%5Cleft(A_2%5Cright)%2B%5Ccdots%0A#card=math&code=%5Cmathbb%20P%5Cleft%28A_1%5Cbigcup%20A_2%5Cbigcup%20%5Ccdots%5Cright%29%5Cleq%20%5Cmathbb%20P%5Cleft%28A_1%5Cright%29%2B%5Cmathbb%20P%5Cleft%28A_2%5Cright%29%2B%5Ccdots%0A&height=35&width=317)

证明

方法 1 数学归纳法

• 当 时，显然 %20%5Cle%20%5Cmathbb%20P(A_1)#card=math&code=%5Cmathbb%20P%28A_1%29%20%5Cle%20%5Cmathbb%20P%28A_1%29)
• 对于 ，如果有：%20%5Cle%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20%7B%5Cmathbb%20P%7D(A_i)#card=math&code=%7B%5Cmathbb%20P%7D%5Cleft%20%28%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7D%20Ai%5Cright%20%29%20%5Cle%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20%7B%5Cmathbb%20P%7D%28Ai%29) ，则由 %20%3D%20%5Cmathbb%20P(A)%20%2B%20%5Cmathbb%7BP%7D(B)%20-%20%5Cmathbb%7BP%7D(A%20%5Ccap%20B)#card=math&code=%5Cmathbb%20P%28A%20%5Ccup%20B%29%20%3D%20%5Cmathbb%20P%28A%29%20%2B%20%5Cmathbb%7BP%7D%28B%29%20-%20%5Cmathbb%7BP%7D%28A%20%5Ccap%20B%29) 可知：%20%3D%5Cmathbb%7BP%7D%5Cleft(%5Cleft%5C%7B%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DAi%5Cright%5C%7D%20%5Cbigcup%20A%7Bn%2B1%7D%5Cright)%20%26%3D%5Cmathbb%7BP%7D%5Cleft(%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DA_i%5Cright)%2B%5Cmathbb%20P%5Cleft(A%7Bn%2B1%7D%5Cright)%20-%20%5Cmathbb%7BP%7D%5Cleft(%5Cleft%5C%7B%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DA_i%5Cright%5C%7D%20%5Cbigcap%20A%7Bn%2B1%7D%5Cright)%5C%5C%0A%09%26%5Cleq%20%5Cmathbb%7BP%7D%5Cleft(%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DA_i%5Cright)%2B%5Cmathbb%20P%5Cleft(A%7Bn%2B1%7D%5Cright)%0A%09%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%09%5Cmathbb%7BP%7D%5Cleft%28%5Cbigcup%7Bi%3D1%7D%5E%7Bn%2B1%7DA_i%5Cright%29%20%3D%5Cmathbb%7BP%7D%5Cleft%28%5Cleft%5C%7B%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DAi%5Cright%5C%7D%20%5Cbigcup%20A%7Bn%2B1%7D%5Cright%29%20%26%3D%5Cmathbb%7BP%7D%5Cleft%28%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DA_i%5Cright%29%2B%5Cmathbb%20P%5Cleft%28A%7Bn%2B1%7D%5Cright%29%20-%20%5Cmathbb%7BP%7D%5Cleft%28%5Cleft%5C%7B%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DA_i%5Cright%5C%7D%20%5Cbigcap%20A%7Bn%2B1%7D%5Cright%29%5C%5C%0A%09%26%5Cleq%20%5Cmathbb%7BP%7D%5Cleft%28%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7DA_i%5Cright%29%2B%5Cmathbb%20P%5Cleft%28A%7Bn%2B1%7D%5Cright%29%0A%09%5Cend%7Bsplit%7D%0A)
• 由数学归纳法可得：%5Cleq%20%5Csum_i%5Cmathbb%20P(A_i)#card=math&code=%5Cmathbb%7BP%7D%5Cleft%28%5Cbigcup_i%20A_i%5Cright%29%5Cleq%20%5Csum_i%5Cmathbb%20P%28A_i%29)

方法 2 将事件转换为独立事件（不相交事件）

假设有 三个事件，则：

• 令 ， 与 不相交
• 令 ， 与 不相交
• 令 #card=math&code=Bi%3DA_i%5Cbackslash%20%5Cleft%28%5Cbigcup%7Bk%3D1%7D%5E%7Bi-1%7D%20A_i%5Cright%29) ，则有 互不相交，且 ，自然 %5Cleq%20P(A_i)#card=math&code=B_i%5Csubset%20A_i%20%5CRightarrow%20P%28B_i%29%5Cleq%20P%28A_i%29) ：

%26%3D%5Cmathbb%20P%5Cleft(B_1%5Ccup%20B_2%5Ccup%20%5Ccdots%5Cright)%3D%5Cmathbb%20P(B_1)%2B%5Cmathbb%20P(B_2)%2B%5Ccdots%20%5C%5C%0A%26%5Cleq%20%5Cmathbb%20P(A_1)%2B%5Cmathbb%20P(A_2)%2B%5Ccdots%0A%5Cend%7Bsplit%7D%0A#card=math&code=%5Cbegin%7Bsplit%7D%0A%5Cmathbb%20P%20%5Cleft%28A_1%5Ccup%20A_2%5Ccup%20%5Ccdots%5Cright%29%26%3D%5Cmathbb%20P%5Cleft%28B_1%5Ccup%20B_2%5Ccup%20%5Ccdots%5Cright%29%3D%5Cmathbb%20P%28B_1%29%2B%5Cmathbb%20P%28B_2%29%2B%5Ccdots%20%5C%5C%0A%26%5Cleq%20%5Cmathbb%20P%28A_1%29%2B%5Cmathbb%20P%28A_2%29%2B%5Ccdots%0A%5Cend%7Bsplit%7D%0A)

马尔可夫不等式 (Markov’s Inequality)

定理

随机变量 ，具有数学期望 ，那么对于任意 ，有：

证明

利用概率和指示函数的等价变换，以及指示函数小于等于 1， 可得：

切尔诺夫界 (Chernoff’s Bounding Method)

定理

令 是一个随机变量，且 ，那么对于 ：

证明

利用马尔可夫不等式可得：

同理可得：

将以上两个不等式综合成一个不等式，得：

霍夫丁引理 (Hoeffding’s Lemma)

定理

对于随机变量 ，：

证明

令 ，且假设 ，有：

因为 是凸函数，根据凸函数的性质，有：

又因为 ，于是：

因为 ，，而 都为 0 的情况没有讨论的意义，所以有 。
令 ，则上式变为：

因为：

所以：

令 ：

定义 ，因为 ，所以 的 对 的取值没有任何限制。可得：

由泰勒中值定理， 使得：

其中：

因此有：

所以：

霍夫丁不等式 (Hoeffding’s Inequality)

定理

假设 服从独立同分布，且 ，，有：

证明

令 ，则：

根据切尔诺夫上界和霍夫丁引理，得：

因为对任意的 都成立，所以对 的二次函数求最小值，得：

概率近似正确 (Probably Approximately Correct, PAC)

：训练集；
：概念（函数），若对训练集 ，有任意 成立，称 为目标概念；
：学得的目标概念构成的集合称为「概念类」
：学习算法；
：算法考虑的所有可能概念的集合称为「假设空间」；
：对于假设空间中的任一概念，由于不能确定它是否真的是目标概念，因此称为「假设」。
：在抽样样本中 的概率；
：在实际所有样本中 的概率；

有限假设空间： 有限；
无限假设空间： 无限；

可分的：训练样本通过学习算法 后，得出假设空间 ， 如果目标概念 ，则假设空间 中存在假设能将所有实例按与真实标记一致的方式完全分开，我们就称该问题对学习算法 是「可分的」；
不可分的：训练样本通过学习算法 后，得出假设空间 ， 如果目标概念 ，则假设空间 中不存在假设能将所有实例按与真实标记一致的方式完全分开，我们就称该问题对学习算法 是「不可分的」；

给定训练集 ，我们希望基于学习算法 学到的模型对应的假设 尽可能接近目标概念 。
以较大的概率学得误差满足预设上限的模型就是「概率」「近似正确」的含义。

PAC 辨识 (PAC Identify)

PAC 辨识：对 ，所有 和分布 ，若存在学习算法 ，其输出假设 满足：

PAC 可学习

PAC 可学习：令 表示从分布 中独立同分布采样得到的样例数目，，对所有分布 ，若存在学习算法 和多项式函数 ，使对于任何 ，算法 能从假设空间 中 PAC 辨识概念类 ，则称概念类 对假设空间 而言是 PAC 可学习的，有时也简称概念类 是 PAC 可学习的。

PAC 学习算法

PAC 学习算法：若学习算法 使概念类 为 PAC 可学习的，且 的运行时间也是多项式函数 的，则称概念类 是高效 PAC 可学习的，称 为概念类 的 PAC 学习算法。

样本复杂度

满足 PAC 学习算法 所需的 中最小的 ，称为学习算法 的样本复杂度。
假定学习算法 处理每个样本的时间为常数，则 的时间复杂度等价于样本复杂度。于是，我们关心的时间复杂度就变成了样本复杂度。

概率近似正确 (PAC)

根据霍夫丁不等式：
假设 服从独立同分布，且 ，，有：

因为：

当 服从伯努利分布时，，代入霍夫丁不等式中，得：

该式表明，当样本数量 足够大，且样本是独立同分布的，那么 与 不会相差很大，它们之间的差值被限定在 之内，把 称为概率近似正确（PAC）。

概率近似正确表明：

• 从样本中 的概率就能推导在所有样本中 的概率；
• 概率上界 完全与 无关，因此目标函数 仍然可以保持未知；
• 不管总体个数是多少，不管总体变量有多么未知，只要给定样本数量 及误差大小 ，就能计算一个「已知到未知」的概率上界；
• 和 在概率上近似正确，如果 很小，那么就能推断出 很小，也就是说在该数据分布下， 与 非常接近，机器学习的模型比较准确。

机器学习的可行性

为了证明机器学习是可行的，就要证明 发生的概率很小，即 很小，进而要证明 很小。
如此看来，只要增大 即可，但事实并非如此。

从单一到有限

以上证明只用了一个固定的假设函数 ，而不是一组假设函数 ，机器没有**学习到任何都东西，只能说验证了固定的假设函数 和目标函数 的差距。
即，只验证了 ，但没有证明 。
因为，当只有一个假设 时，它的训练误差是客观存在的，只能验证它，却不能减小它。减小误差才是学习**。
于是，需要一种方式证明 。

从一组假设函数 中选出一个使得 最小的假设函数，并将这个最优假设函数设定为 。
根据布尔不等式（联合上界）及霍夫丁不等式，可得：

当假设函数的个数 是有限的，只要增大 就可以让 很小，机器学习是可行的。

从有限到无限

实际问题中，假设函数的个数 通常是无限的。此时即便 很大， 也会很大。

从无限到有限

事实上，很多假设函数的效果是相同的，而且推导过程中使用的联合上界会使上界过于宽松**。
**
即导致：

不等式右边的数值过大。

等效假设函数

很多假设函数的效果是相同的，这些等效的假设被归结为等效的一类（等效类），而增长函数 是计算等效类的个数。
因为增长函数的上界是 ，所以用 来代替上面不等式中的 ，得到：

分子分母均为 形式，分子分母为等价无穷大（当 时，分子分母趋于无穷大的速率一样），但 通常比 大，因此最后的比值会比 1 大。然而概率是小于或等于 1 的数。因此若分子是分母的低阶无穷大，问题就解决了。

根据增长函数的上界，可知：

于是：

根据洛必达法则，对 阶多项式函数和指数函数分别求 次导数后，分子为常数，分母还是与 相关的指数函数，这样，当 很大时，整体会很小。综上所述：

机器学习可行。

上式为 VC 不等式的仿真版，真正的 VC 不等式如下：

• 仿真版：

• 真正版：

VC 不等式 (Vapnik-Chervonenkis Inequality)

符号

, ,
：frequency of agreement of on
：frequency of agreement of on
：probability of agreement of
：a learning model
：the number of different patterns of on
：the growth function of
：a subset of that 「represents」

：is w.r.t. . Thus,
：is a short-hand of

基础不等式

霍夫丁不等式

Bin model

注意峰值出现在 ，如果 是整数，对于 ，易证：

引理 1 (Bounding the deviation with two half-vectors)

for such that

证明引理 1

引理 2 (Bounding the difference of half-vectors under specific conditions)

对于任意整数 ， 从 到 ，有：

证明引理 2

因为：

所以，左式（left-hand-side，LHS） 独立于 ，
如果 ，则：

因为左式独立于 ，于是可以处理一个伪问题，其中， 是从 中得出的，并且不失一般性地选择 使 ，于是：

所以：

其中，

注意到 的峰值出现在 附近。令：

于是：

现在，

注意到需要 ，而当集合 非空时，；如果集合为空，左式等于 0，引理无意义。

定理 (VC 不等式)

对于满足引理 1 的 ，有：

证明 (VC 不等式)

由引理 1 可得：

We get the same probability if we first generate according to and choose one of the permutations of to permute into . Here depends on and the permutation , but and are equivalent.

VC 上界

VC 不等式右边的项 被称为 VC 上界。

VC 维 (VC Dimension)

给定数据集 有 个点以及假设函数空间 ，突破点 表示第一个无法被打散的点，既然 点是第一个无法被打散的点，那么 点一定是最后被打散的点。通常把它定义为 VC 维（VC Dimension），有：

把 VC 维代入 VC 不等式中，即用 替代 ，得到：

只要 是有限的，那么当 很大时，不等式的最右边就是一个很小的数，即真实误差 逼近训练误差 ，那么假设函数 具有很好的推广能力。

机器学习可行的本质

由 VC 不等式可知，「有限的 VC 维才是机器学习可行的条件」，从而有以下结论：

• 不需要知道算法
• 不需要知道数据分布
• 不需要知道目标函数
• 只需要知道训练集 和假设函数集 就能找到最优假设函数 来学习

模型复杂度 (Model Complexity)

设定一个概率 ，则样本数 和容忍度 之间的关系为：

可得：

因此，在大于 的概率下：

可得：

定义 ， 为惩罚函数，也被称为模型复杂度（Model Complexity）。
于是可得：

表示假设空间 越强，算法越需要强大的推广能力。即， 容量越大， 越大，那么模型就越难学习。

真实误差 = 训练误差 + 模型复杂度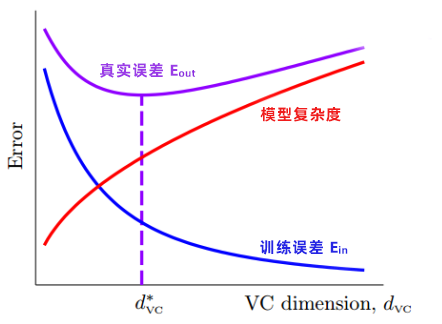

训练误差是 的减函数；而模型复杂度是 的增函数。
机器学习的任务就是找到有最佳 VC 维 的模型，对应着最小的真实误差。

样本复杂度 (Sampling Complexity)

设定一个容忍度 ，计算需要的样本数量 ，即计算出样本复杂度（Sampling Complexity）：
根据：

得到：

上式左右两边都有 ，因此需要用迭代法（如牛顿法）求解。

通过迭代法算出：

• 理论上，样本数量
• 实际上，样本数量

原因如下：

• 霍夫丁不等式适用于任何数据分布和任何目标函数；
• 增长函数适用于任何数据；
• VC 维适用于任何假设空间；
• 联合上界适用于最差的状况。

实践中，「任何」和「最差」同时发生的可能性不大，因此，样本复杂度的理论值和实际值可能相差很大。

通用近似定理/万能近似定理 (Universal Approximation Theorem)

白话定理

在人工神经网络的数学理论中， 通用近似定理（或称万能近似定理）指出人工神经网络可以用来近似任意函数。 通常此定理所指的神经网络为前馈神经网络，并且被近似的目标函数通常为输入输出都在欧几里得空间的连续函数。但亦有研究将此定理扩展至其他类型的神经网络。

此定理意味着神经网络可以用来近似任意的复杂函数，并且可以达到任意近似精准度。但它并没有告诉我们如何选择神经网络参数（权重、神经元数量、神经层层数等等）来达到我们想近似的目标函数。

数学描述

任意宽度

任意宽度和有限深度的万能近似定理的经典形式如下：

固定一个连续函数 和正整数 ，对于任意连续函数 ，任意 的紧致子集（compact subset），任意的 ，当且仅当存在一个可以表示为 的连续函数 时，函数 不是一个多项式函数。
其中， 表示合成的仿射映射（composable affine maps ）； 表示逐成分合成（component-wise composition），使得近似界（approximation bound）成立：

该定理指出，第一层可以逼近任何表现良好的函数。这样一个表现良好的函数也可以由一个和第一层结构相同并且其后各层近似为恒等函数的更深的网络近似。

任意深度

这个定理的「对偶」版本考虑了有限宽度和任意深度的网络。
该定理指出，在网络深度允许增加的情况下，带有 ReLU 激活函数的宽度为 的网络可以在 L1 距离上近似于 维输入空间上的任意勒贝格可积函数（Lebesgue integrable function ）。当宽度小于或等于 时，其表达能力是有限的，除了零测度集外，所有勒贝格可积函数（Lebesgue integrable function ）都不能用宽度为 的 ReLU 网络近似。宽度为 的 ReLU 网络足以逼近任意 维输入变量的连续函数。

Universal approximation theorem (L1 distance, ReLU activation, arbitrary depth)

对于任意勒贝格可积函数（Lebesgue integrable function ） 和任意的 ，存在一个宽度为 的全连接 ReLU 网络 （用函数 表示该网络），使下式成立：

Universal approximation theorem (nonaffine activation, arbitrary depth)

令 表示任意连续可微的非仿射连续函数，该函数至少在一点上具有非零导数；令 是紧致的； 上的实向量-值（real vector-valued）连续函数的空间表示为 ；令 表示有 个输入神经元、 个输出神经元和任意数量的隐层，每个隐层有 个神经元，每个隐神经元都有激活函数 ，每个输出神经元都有同样的激活函数作为其自身的激活函数。给定任意的 以及任意的 ，存在 ，对于所有的 ，使得下式成立：

换句话说，相对于一致范数（uniform norm）， 在 中是稠密的。

定理证明

• 神经网络万能近似定理的可视化证明：A visual proof that neural nets can compute any function
• 多层感知器（即至少有一个隐藏层的前馈神经网络，假设神经网络使用的是 Sigmoid 激活函数）可以逼近任意连续函数：Approximation by superpositions of a sigmoidal function
• 不一定用 Sigmoid 激活函数，但只有某些激活函数不能使神经网络万能逼近：Multilayer Feedforward Networks With a Nonpolynomial Activation Function Can Approximate Any Function.pdf；Approximation theory of the MLP model in neural networks.pdf
• 当神经网络的深度足够大时，卷积神经网络能够以任意精度逼近任何连续函数：Universality of Deep Convolutional Neural Networks.pdf
• 递归神经网络是通用函数逼近器：Recurrent Neural Networks Are Universal Approximators.pdf

信息瓶颈理论 (Information Bottleneck Method)

白话定理

信息瓶颈是信息论中的一种方法，运用了互信息的概念。对于一随机变量 ，假设已知 与观察变量 之间的联合概率分布为 。此时，当需要概括（聚类） 时，可以通过信息瓶颈方法来分析如何最优化地平衡准确度与复杂度（数据压缩）。该方法的应用还包括分布聚类（distributional clustering）与降维等。此外，信息瓶颈也被用于分析深度学习的过程。

数学描述

假设压缩后的随机变量为 ，试图用 代替 来预测 。此时，可使用以下算法得到最优的 ：

其中， 和 分别为 与 之间的互信息、 与 之间的互信息，可由 计算得到；
为示拉格朗日乘数。

小数定律 (Law of Small Numbers, LSN)

小数定律是阿莫斯·特沃斯基（Amos Tversky）和丹尼尔·卡纳曼（Daniel Kahneman）在其研究中对「赌徒谬误」的总结。

白话定理

如果统计数据很少，那么事件就表现为各种极端情况，而这些情况都是偶然事件，跟它的期望值没有一点关系。

大数定律 (Law of Large Numbers, LLN)

白话定理

如果统计数据足够大，那么事物出现的频率就能无限接近它的期望。
样本数量越多，则样本的算术平均值就有越高的概率接近其期望值（总体均值）。
我们通常对数据进行抽样估计利用的就是大数定理思想。
**

大数定律的作用

大数定律告诉我们，当样本容量极大时，样本均值约等于总体期望，即 ，因此我们可以用样本均值来估计总体的期望。

数学描述

设 是一列独立同分布（i.i.d）的可积随机变量，均值 存在，，方差 ，则则对于任意的正数 ，有：

或：

实际上，我们只需要均值 存在即有大数定律成立，上述定理中加上了方差存在的条件，只是为了证明的方便。

弱大数定理

设 是一列独立同分布（i.i.d）的可积随机变量，期望 存在，

称 依概率收敛于期望 ，此即为弱大数定律。
**

强大数定理

设 是一列独立同分布（i.i.d）的可积随机变量，期望 存在，

称 以概率 1 收敛于期望 ，又称 几乎处处收敛于
**

定理证明

假设随机变量 X 具有数学期望 ，方差为 ，样本均值 ，根据切比雪夫不等式：

因为：


代入切比雪夫不等式得到：

因为 ，所以：

Chebyshev 大数定律

前提条件： 相互独立（不必同分布）； 存在且一致有上界（即， 使 对于一切 成立）。
结论：

数学意义：算数平均值依概率收敛于数学期望。

Bernoulli 大数定律

前提条件： 是 n 重 Bernoulli 试验中事件 A 的发生次数；每次试验 A 发生的概率为 p。（即， 相互独立且都服从于参数为 的 Bernoulli 分布（0-1 分布））
结论：

数学意义：频率依概率收敛于统计概率。
Bernoulli 大数定律属于 Chebyshev 大数定律的一种特殊情况，可以由 Chebyshev 大数定律推出。

Khinchin 大数定律

前提条件： 相互独立且同分布； 存在
结论：

数学意义：算数平均值依概率收敛于数学期望。
Chebyshev 大数定律要求独立和方差有上界；Khinchin 大数定律要求独立同分布和期望存在。

中心极限定理 (Central Limit Theorem, CLT)

白话定理

大量相互独立的随机变量，其均值（或者和）的分布以正态分布为极限。
中心极限定理指的是给定一个任意分布的总体，每次从总体中随机抽取 n 个抽样，一共抽 m 次， 然后把这 m 组抽样分别求出平均值， 这些平均值的分布接近正态分布。
中心极限定理说明：

1. 样本的平均值约等于总体的平均值
   
2. 不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体平均值周围，并且呈正态分布

中心极限定理的作用

1. 在没有办法得到总体全部数据的情况下，可以用样本来估计总体
   如果知道了某个正确抽取的样本的平均值和标准差，就能估计出总体的平均值和标准差。
2. 根据总体的平均值和标准差，判断某个样本是否属于总体
   如果知道了某个总体的具体信息，以及某个样本的数据，就能推理出该样本是否是该群体的样本之一。通过中心极限定理的正态分布，就能计算出某个样本属于总体的概率是多少。如果概率非常低，那么我们就能自信地认为该样本不属于该群体。这也是统计概率中假设检验的原理。

数学描述

设 是一列独立同分布（i.i.d）的可积随机变量，期望 存在，方差 存在，，

即，当 时，
即，样本容量极大时，样本均值的抽样分布趋近于期望为 、标准差为 的正态分布。
大数定律和中心极限定理都是讲样本均值的分布的估计，只不过是相比大数定律，中心极限定理更精确，当然前提条件也比大数定律的强。

棣莫佛－拉普拉斯定理

棣莫佛－拉普拉斯（de Moivre - Laplace）定理是中央极限定理的最初版本，讨论了服从二项分布的随机变量序列。它指出，参数为 的二项分布以 为均值、 为方差的正态分布为极限。

若 是 次伯努利实验中事件 出现的次数，每次试验成功的概率为 ，且 ，则对任意有限区间 ：
令 ，当 时：

其中， 为标准正态分布的概率密度函数

林德伯格－列维定理

定理描述

林德伯格－列维（Lindeberg-Levy）定理，是棣莫佛－拉普拉斯定理的扩展，讨论独立同分布随机变量序列的中央极限定理。它表明，独立同分布(iid independent and indentically distributed)、且数学期望和方差有限的随机变量序列的标准化和以标准正态分布为极限：
设随机变量 独立同分布，且具有有限的数学期望和方差 ，。记：，则：

即：

其中 是标准正态分布的分布函数。

定理证明

记 的特征函数为 ，根据傅里叶变换，样本空间中的褶积在特征函数空间变为乘积，因此 的特征函数为 ，由于 ，故 ，因此：

所以：

由于 是连续函数，它对应的分布函数为 ，因此由逆极限定理知：

林德伯格-费勒定理

定理描述

林德伯格－费勒定理，是中心极限定理的高级形式，是对林德伯格－列维定理的扩展，讨论独立，但不同分布的情况下的随机变量和。它表明，满足一定条件时，独立，但不同分布的随机变量序列的标准化和依然以标准正态分布为极限：
记随机变量序列 （独立但不一定同分布， 且有有限方差）部分和为 ，记 ，，如果对每个 ，序列满足：

则称它满足林德伯格（Lindeberg）条件。满足此条件的序列趋向于正态分布，即：

同时，该条件也是期望为零、方差有限的独立变量之和趋于正态分布的必要条件。与之相关的是李雅普诺夫（Lyapunov）条件：

满足李雅普诺夫条件的序列，必满足林德伯格条件。

定理证明

在此只对较强的李雅普诺夫条件给出证明。
以下证明对每一实数 ，特征函数满足

泰勒展开，上式可近似为：

由李雅普诺夫条件，当 时，第一项收敛于零。
令 ，则由李雅普诺夫不等式得：

因此第二项也收敛于零。

小数定理、大数定理和中心极限定理的关系

覆盖定理 (Cover’s Theorem)

白话定理

Cover’s Theorem 是核方法的理论基础，指的是对于非线性可分的训练集，可以大概率通过将其非线性映射到一个高维空间来转化成线性可分的训练集。

定理证明

使用确定性映射：假设有 样本，将它们升维到 维实空间中单纯形的顶点上。由于每个样本都是线性可分的，所以定理得证。

附件

Learning from data a short course.pdf
vc proof.pdf
note_hoeffding.pdf
Concentration Inequalities Hoeffding and McDiarmid.pdf
Hoefding’s Inequality.pdf
McDiarmid’s Inequality.pdf

参考资料

1. 《机器学习》
2. 《快乐机器学习》：P44（NFL 定理的解释）
3. NFL定理：https://www.jianshu.com/p/e1705306f6a3
4. 没有免费午餐定理通俗证明：https://zhuanlan.zhihu.com/p/48493722
5. Inductive bias：https://en.wikipedia.org/wiki/Inductive_bias
6. Relational inductive biases, deep learning, and graph network：https://zhuanlan.zhihu.com/p/38861547
7. 如何理解 Inductive bias？：https://www.zhihu.com/question/264264203
8. 林轩田《机器学习基石》、《机器学习技法》
9. Learning from data: a short course
10. VC proof
11. 通用近似定理：https://ai.stackexchange.com/questions/13317/where-can-i-find-the-proof-of-the-universal-approximation-theorem
12. 信息瓶颈：https://zh.wikipedia.org/wiki/信息瓶颈
13. Information bottleneck method：https://en.wikipedia.org/wiki/Information_bottleneck_method
14. Cover’s theorem：https://en.wikipedia.org/wiki/Cover%27s_theorem