在做分类时常常需要估算不同样本之间的相似性度量 (Similarity Measurement)，这时通常采用的方法就是计算样本间的“距离” (Distance)。

欧氏距离 (Euclidean Distance)

(1) 二维平面上两点 a(x1,y1) 与 b(x2,y2) 间的欧氏距离：

%5E%7B2%7D%2B%5Cleft(y%7B1%7D-y%7B2%7D%5Cright)%5E%7B2%7D%7D%0A#card=math&code=d%7B12%7D%3D%5Csqrt%7B%5Cleft%28x%7B1%7D-x%7B2%7D%5Cright%29%5E%7B2%7D%2B%5Cleft%28y%7B1%7D-y_%7B2%7D%5Cright%29%5E%7B2%7D%7D%0A&height=35&width=230)
(2) 三维空间两点 a(x1,y1,z1) 与 b(x2,y2,z2) 间的欧氏距离：

%5E%7B2%7D%2B%5Cleft(y%7B1%7D-y%7B2%7D%5Cright)%5E%7B2%7D%2B%5Cleft(z%7B1%7D-z%7B2%7D%5Cright)%5E%7B2%7D%7D%0A#card=math&code=d%7B12%7D%3D%5Csqrt%7B%5Cleft%28x%7B1%7D-x%7B2%7D%5Cright%29%5E%7B2%7D%2B%5Cleft%28y%7B1%7D-y%7B2%7D%5Cright%29%5E%7B2%7D%2B%5Cleft%28z%7B1%7D-z_%7B2%7D%5Cright%29%5E%7B2%7D%7D%0A&height=35&width=324)
(3) 两个 n 维向量 a(x11,x12,…,x1n) 与 b(x21,x22,…,x2n) 间的欧氏距离：

%5E%7B2%7D%7D%0A#card=math&code=d%7B12%7D%3D%5Csqrt%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%28x%7B1%20k%7D-x%7B2%20k%7D%5Cright%29%5E%7B2%7D%7D%0A&height=54&width=177)
向量运算的形式：

(a-b)%5E%7BT%7D%7D%0A#card=math&code=d_%7B12%7D%3D%5Csqrt%7B%28a-b%29%28a-b%29%5E%7BT%7D%7D%0A&height=35&width=171)

曼哈顿距离 (Manhattan Distance)

想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源， 曼哈顿距离也称为城市街区距离(City Block distance)。

(1) 二维平面两点 a(x1,y1) 与 b(x2,y2) 间的曼哈顿距离：

(2) 两个 n 维向量 a(x11,x12,…,x1n) 与 b(x21,x22,…,x2n) 间的曼哈顿距离：

切比雪夫距离 (Chebyshev Distance)

国际象棋中国王走一步能够移动到相邻的 8 个方格中的任意一个，那么国王从格子 (x1,y1) 走到格子 (x2,y2) 最少需要多少步？最少步数总是 max( | x2-x1 | , | y2-y1 | ) 步 。有一种类似的一种距离度量方法叫切比雪夫距离。

(1) 二维平面两点 a(x1,y1) 与 b(x2,y2) 间的切比雪夫距离：

%0A#card=math&code=d%7B12%7D%3Dmax%28%5Cleft%7Cx%7B1%7D-x%7B2%7D%5Cright%7C%2C%5Cleft%7Cy%7B1%7D-y_%7B2%7D%5Cright%7C%29%0A&height=20&width=227)

(2) 两个 n 维向量 a(x11,x12,…,x1n) 与 b(x21,x22,…,x2n) 间的切比雪夫距离：

%0A#card=math&code=d%7B12%7D%3Dmax%7Bi%7D%28%5Cleft%7Cx%7B1i%7D-x%7B2i%7D%5Cright%7C%29%0A&height=20&width=169)
这个公式的另一种等价形式是：

%5E%7B1%20%2F%20k%7D%0A#card=math&code=%5Cmathrm%7Bd%7D%7B12%7D%3D%5Clim%20%7Bk%20%5Crightarrow%20%5Cinfty%7D%5Cleft%28%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft%7Cx%7B1%20i%7D-x_%7B2%20i%7D%5Cright%7C%5E%7Bk%7D%5Cright%29%5E%7B1%20%2F%20k%7D%0A&height=57&width=232)

用放缩法和夹逼法则来证明

闵可夫斯基距离 (Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义。

(1) 闵氏距离的定义

两个 n 维变量 a(x11,x12,…,x1n) 与 b(x21,x22,…,x2n) 间的闵可夫斯基距离定义为：

• 当 时，就是曼哈顿距离
• 当 时，就是欧氏距离
• 当 时，就是切比雪夫距离

根据变参数的不同，闵氏距离可以表示一类的距离

(2) 闵氏距离的缺点

闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。

举个例子：二维样本(身高,体重)，其中身高范围是150-190，体重范围是 50~60，有三个样本：a(180,50)，b(190,50)，c(180,60)。那么 a 与 b 之间的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于 a 与 c 之间的闵氏距离，但是身高的 10cm 真的等价于体重的 10kg 么？因此用闵氏距离来衡量这些样本间的相似度很有问题。

简单说来，闵氏距离的缺点主要有两个：

1. 将各个分量的量纲 (scale)，也就是“单位”当作相同的看待了
2. 没有考虑各个分量的分布（期望，方差等）可能是不同的

标准化欧氏距离 (Standardized Euclidean Distance)

(1) 标准欧氏距离的定义

标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路：既然数据各维分量的分布不一样，那我先将各个分量都“标准化”到均值、方差相等，而且标准化后变量的数学期望为 0，方差为 1。因此样本集的标准化过程 (standardization) 用公式描述就是：

经过简单的推导就可以得到两个 n 维向量 a(x11,x12,…,x1n) 与 b(x21,x22,…,x2n) 间的标准化欧氏距离的公式：

%5E%7B2%7D%7D%0A#card=math&code=d%7B12%7D%3D%5Csqrt%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%28%5Cfrac%7Bx%7B1%20k%7D-x%7B2%20k%7D%7D%7Bs_%7Bk%7D%7D%5Cright%29%5E%7B2%7D%7D%0A&height=55&width=195)

如果将方差的倒数看成是一个权重，这个公式可以看成是一种 加权欧氏距离 (Weighted Euclidean distance)。

兰氏距离 / 堪培拉距离 (Lance and Williams Distance / Canberra Distance)

兰氏距离 (Lance and Williams distance)，又称堪培拉距离 (Canberra Distance)，被认为是曼哈顿距离的加权版本。其定义公式为：

通常兰氏距离对于接近于 0（大于等于 0）的值的变化非常敏感，对数据的量纲不敏感。兰氏距离假定变量之间相互独立，没有考虑变量之间的相关性。

马氏距离 (Mahalanobis Distance)

(1) 马氏距离定义
有 M 个样本向量 X1~Xm ，协方差矩阵记为 S，均值记为向量 μ，则其中样本向量 X 到 u 的马氏距离表示为：

%3D%5Csqrt%7B(X-%5Cmu)%5E%7BT%7D%20S%5E%7B-1%7D(X-%5Cmu)%7D%0A#card=math&code=%5Cmathrm%7BD%7D%28%5Cmathrm%7BX%7D%29%3D%5Csqrt%7B%28X-%5Cmu%29%5E%7BT%7D%20S%5E%7B-1%7D%28X-%5Cmu%29%7D%0A&height=35&width=232)

而其中向量 Xi 与 Xj 之间的马氏距离定义为：

%3D%5Csqrt%7B(X_i-X_j)%5E%7BT%7D%20S%5E%7B-1%7D(X_i-X_j)%7D%0A#card=math&code=%5Cmathrm%7BD%7D%28%5Cmathrm%7BX_i%2CX_j%7D%29%3D%5Csqrt%7B%28X_i-X_j%29%5E%7BT%7D%20S%5E%7B-1%7D%28X_i-X_j%29%7D%0A&height=35&width=293)

若协方差矩阵是单位矩阵（各个样本向量之间独立同分布），则公式就成了：

%3D%5Csqrt%7B(X_i-X_j)%5E%7BT%7D(X_i-X_j)%7D%0A#card=math&code=%5Cmathrm%7BD%7D%28%5Cmathrm%7BX_i%2CX_j%7D%29%3D%5Csqrt%7B%28X_i-X_j%29%5E%7BT%7D%28X_i-X_j%29%7D%0A&height=35&width=266)

也就是欧氏距离。
若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离。

(2) 马氏距离的优缺点：量纲无关，排除变量之间的相关性的干扰。

巴氏距离 (Bhattacharyya Distance)

在统计中，Bhattacharyya 距离测量两个离散或连续概率分布的相似性。它与衡量两个统计样品或种群之间的重叠量的 Bhattacharyya 系数密切相关。Bhattacharyya 距离和 Bhattacharyya 系数以 20 世纪 30 年代曾在印度统计研究所工作的一个统计学家 A. Bhattacharya 命名。同时，Bhattacharyya 系数可以被用来确定两个样本被认为相对接近的，它是用来测量类之间的可分离性。

（1）巴氏距离的定义

对于离散概率分布 p 和 q 在同一域 X，它被定义为：

其中， 是 Bhattacharyya 系数（巴氏系数）：

(2) Bhattacharyya 系数
对于连续概率分布，Bhattacharyya 系数被定义为：

对于离散概率分布，Bhattacharyya 系数被定义为：

两种情形中 ，巴氏距离 均不服从三角不等式，但 服从三角不等式。
对于多变量的高斯分布 #card=math&code=p_i%3DN%28m_i%2CP_i%29&height=20&width=110)：

%5ETP%5E%7B-1%7D(m_1-m_2)%2B%5Cfrac%7B1%7D%7B2%7D%20ln%5Cleft(%5Cfrac%7Bdet%5C%20P%7D%7B%5Csqrt%7Bdet%5C%20P_1%5C%20det%5C%20P_2%7D%7D%5Cright)%0A#card=math&code=D_B%3D%5Cfrac%7B1%7D%7B8%7D%28m_1-m_2%29%5ETP%5E%7B-1%7D%28m_1-m_2%29%2B%5Cfrac%7B1%7D%7B2%7D%20ln%5Cleft%28%5Cfrac%7Bdet%5C%20P%7D%7B%5Csqrt%7Bdet%5C%20P_1%5C%20det%5C%20P_2%7D%7D%5Cright%29%0A&height=54&width=456)

其中， 和 分别是分布的均值和协方差，并且

巴氏距离中的第一项与马氏距离相关

Bhattacharyya 系数是两个统计样本之间重叠量的近似测量，巴氏系数可用来对两组样本的相关性进行测量。

计算巴氏系数涉及到对这两个样本的重叠部分进行基本形式的积分。两个样本值的积分被分成指定数目的部分。而每一个样本的每一个部分的成员数被用于下式中：

其中，、 为两个样本， 是分块数。

这样一来，这个式子就会随着某块中有两个样本的公共成员而变大，也会随着某块中有一大片重叠的样本成员而变大。分块数的选定依赖于样本中的成员数量；如果分块太少会因高估了重叠区域而失去精确性，如果分块太多会因为造成空块而失去精确性。

如果两个样本完全没有重叠，巴氏系数将会等于 0，因为每一个分块都将被 0 乘。这意味着完全分离的样本不能被巴氏系数单独测定出来。

海林格距离 (Hellinger Distance)

Hellinger Distance 被用来衡量两个概率分布之间的相似性，属于 f-divergence 的一种。

f-divergence 是一个函数 Df(P||Q) 用来衡量两个概率分布 P 和 Q 之间的不同

Hellinger 距离服从三角不等式。

余弦相似度 (Cosine Similarity)

几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。

(1) 在二维空间中向量 a(x1,y1) 与向量 b(x2,y2) 的夹角余弦公式：

(2) 两个 n 维样本点 a(x11,x12,…,x1n) 和 b(x21,x22,…,x2n) 的夹角余弦：

%3D%5Cfrac%7B%5Cboldsymbol%7Ba%7D%5ET%5Cboldsymbol%7Bb%7D%7D%7B%7C%5Cboldsymbol%7Ba%7D%7C%5Ccdot%7C%5Cboldsymbol%7Bb%7D%7C%7D%0A#card=math&code=cos%28%5Ctheta%29%3D%5Cfrac%7B%5Cboldsymbol%7Ba%7D%5ET%5Cboldsymbol%7Bb%7D%7D%7B%7C%5Cboldsymbol%7Ba%7D%7C%5Ccdot%7C%5Cboldsymbol%7Bb%7D%7C%7D%0A&height=47&width=123)

即：

%3D%5Cfrac%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%20x%7B1%20k%7D%20x%7B2%20k%7D%7D%7B%5Csqrt%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%20x%7B1%20k%7D%5E%7B2%7D%7D%20%5Csqrt%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%20x%7B2%20k%7D%5E%7B2%7D%7D%7D%0A#card=math&code=%5Ccos%20%28%5Ctheta%29%3D%5Cfrac%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%20x%7B1%20k%7D%20x%7B2%20k%7D%7D%7B%5Csqrt%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%20x%7B1%20k%7D%5E%7B2%7D%7D%20%5Csqrt%7B%5Csum%7Bk%3D1%7D%5E%7Bn%7D%20x%7B2%20k%7D%5E%7B2%7D%7D%7D%0A&height=62&width=239)

• %3D1#card=math&code=cos%28%5Ctheta%29%3D1&height=20&width=74) 相似度最高，同向，夹角为 0°
• %3D0#card=math&code=cos%28%5Ctheta%29%3D0&height=20&width=74) 相似度低，垂直，夹角为 90°
• %3D-1#card=math&code=cos%28%5Ctheta%29%3D-1&height=20&width=88) 相似度最低，反向，夹角为 180°

汉明距离 (Hamming Distance)

(1) 汉明距离的定义

两个等长字符串 s1 与 s2 之间的汉明距离定义为：将其中一个变为另外一个所需要做的最小替换次数。

例如：

• 10**111**01与10**010**01之间的汉明距离是2。
• 2**1438**96与2**2337**96之间的汉明距离是3。
• “t**one**d“与”r**ose**s“之间的汉明距离是3。

应用：信息编码（为了增强容错性，应使得编码间的最小汉明距离尽可能大）。

(2) 汉明重量的定义

汉明重量是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。

莱文斯坦距离 (Levenshtein Distance)

(1) 莱文斯坦距离的定义

Levenshtein距离，是编辑距离的一种。指两个字串之间，由一个转成另一个所需的最少编辑操作次数。
允许的编辑操作包括：

1. 将一个字符替换成另一个字符
2. 插入一个字符
3. 删除一个字符

如果分别用 |a| 和 |b| 表示 a,b 两个字符串的长度，那么它们的列文斯坦距离为 ，它符合：

是一个指示函数（indicator function），当 时，其值为 0，其他时候它等于 1 。
表示 a 的前 i 个字符与 b 的前 j 个字符之间的列文斯坦距离。（i 和 j 都是从 1 开始的下标）

• min 运算中的第一个公式代表（从 a 中）删除字符（以到达 b）
• 第二个公式代表插入字符
• 第三个代表替换（取决于当前字符是否相同）

例如：将“kitten”一字转成“sitting”的莱文斯坦距离为3：

1. kitten → sitten （k→s）
2. sitten → sittin （e→i）
3. sittin → sitting （插入g）

(2) 莱文斯坦距离的详细解释

对于两个字符串 s 和 t，当 s[i] == t[j] 时，我们继续考察 s[i+1] 和 t[j+1]；当 s[i] != t[j] 时，我们有下述选择：

• 删除 s[i] 或者在 t 中增加一个与 s[i] 相同的字符， 继续考察 s[i+1] 和 t[j]；
• 删除 t[j] 或者在 s 中增加一个与 t[j] 相同的字符， 继续考察 s[i] 和 t[j+1]；
• 替换 s[i] 为 t[j] 或者 t[j] 为 s[i]， 继续考察 s[i+1] 和 t[j+1]；

我们定义 edist[i][j] 表示子串 s[0, i] 与 t[0, j] 的最小编辑距离，那么由上面的分析可知，edist[i][j] 可以由 edist[i-1][j]、edist[i][j-1] 和 edist[i-1][j-1] 这三个状态转化而来：

• 当 edist[i][j] 由 edist[i-1][j] 转化而来的时候，我们只能通过删除 s[i] 或者在 t 中增加一个与 s[i] 相同的字符，那么编辑距离一定增 1
• 当 edist[i][j] 由 edist[i][j-1] 转化而来的时候，我们只能通过删除 t[j] 或者在 s 中增加一个与 t[j] 相同的字符，那么编辑距离一定增 1
• 当 edist[i][j] 由 edist[i-1][j-1] 转化而来的时候
  • 如果 s[i] == t[j] ，编辑距离保持不变
  • 如果 s[i] != t[j] ，我们只能替换 s[i] 为 t[j] 或者 t[j] 为 s[i]，编辑距离增 1

最终的 edist[i][j] 取这三者中最小的一个即可，所以我们有：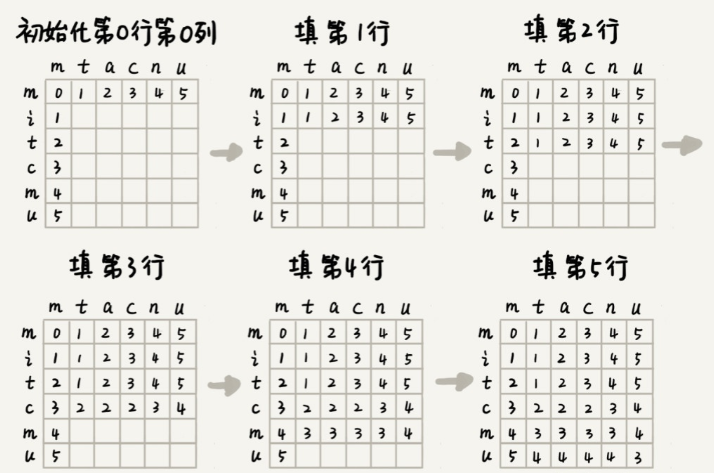

杰卡德相似系数 (Jaccard Similarity Coefficient)

(1) 杰卡德相似系数

两个集合 A 和 B 的交集元素在 A，B 的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号 J(A,B) 表示。

%3D%5Cfrac%7B%7CA%5Ccap%20B%7C%7D%7B%7CA%5Ccup%20B%7C%7D%0A#card=math&code=J%28A%2CB%29%3D%5Cfrac%7B%7CA%5Ccap%20B%7C%7D%7B%7CA%5Ccup%20B%7C%7D%0A&height=47&width=138)

杰卡德相似系数是衡量两个集合的相似度一种指标。

(2) 杰卡德距离

与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示：

%3D1-J(A%2C%20B)%3D%5Cfrac%7B%7CA%20%5Ccup%20B%7C-%7CA%20%5Ccap%20B%7C%7D%7B%7CA%20%5Ccup%20B%7C%7D%0A#card=math&code=%5Cmathrm%7BJ%7D_%7B%5Cdelta%7D%28%5Cmathrm%7BA%7D%2C%20%5Cmathrm%7BB%7D%29%3D1-J%28A%2C%20B%29%3D%5Cfrac%7B%7CA%20%5Ccup%20B%7C-%7CA%20%5Ccap%20B%7C%7D%7B%7CA%20%5Ccup%20B%7C%7D%0A&height=47&width=325)

杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

(3) 杰卡德相似系数与杰卡德距离的应用

可将杰卡德相似系数用在衡量样本的相似度上。
样本 A 与样本 B 是两个 n 维向量，而且所有维度的取值都是 0 或 1 。
例如：A(0111) 和 B(1011)。我们将样本看成是一个集合，1 表示集合包含该元素，0 表示集合不包含该元素。

• p ：样本 A 与 B 都是 1 的维度的个数
• q ：样本 A 是 1，样本 B 是 0 的维度的个数
• r ：样本 A 是 0，样本 B 是 1 的维度的个数
• s ：样本 A 与 B 都是 0 的维度的个数

那么样本A与B的杰卡德相似系数可以表示为：

这里 p+q+r 可理解为 A 与 B 的并集的元素个数，而 p 是 A 与 B 的交集的元素个数。
而样本 A 与 B 的杰卡德距离表示为：

（皮尔逊）相关系数 (Correlation Coefficient ) 与相关距离 (Correlation Distance)

(1) 相关系数的定义
%7D%7B%5Csigma%7BX%7D%20%5Csigma%7BY%7D%7D%3D%5Cfrac%7BE%5Cleft%5B%5Cleft(X-%5Cmu%7BX%7D%5Cright)%5Cleft(Y-%5Cmu%7BY%7D%5Cright)%5Cright%5D%7D%7B%5Csigma%7BX%7D%20%5Csigma%7BY%7D%7D%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft(X%7Bi%7D-%5Cmu%7BX%7D%5Cright)%5Cleft(Y%7Bi%7D-%5Cmu%7BY%7D%5Cright)%7D%7B%5Csqrt%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft(X%7Bi%7D-%5Cmu%7BX%7D%5Cright)%5E%7B2%7D%7D%20%5Csqrt%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft(Y%7Bi%7D-%5Cmu%7BY%7D%5Cright)%5E%7B2%7D%7D%7D%0A#card=math&code=%5Crho%7BX%20Y%7D%3D%5Cfrac%7B%5Coperatorname%7Bcov%7D%28X%2C%20Y%29%7D%7B%5Csigma%7BX%7D%20%5Csigma%7BY%7D%7D%3D%5Cfrac%7BE%5Cleft%5B%5Cleft%28X-%5Cmu%7BX%7D%5Cright%29%5Cleft%28Y-%5Cmu%7BY%7D%5Cright%29%5Cright%5D%7D%7B%5Csigma%7BX%7D%20%5Csigma%7BY%7D%7D%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft%28X%7Bi%7D-%5Cmu%7BX%7D%5Cright%29%5Cleft%28Y%7Bi%7D-%5Cmu%7BY%7D%5Cright%29%7D%7B%5Csqrt%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft%28X%7Bi%7D-%5Cmu%7BX%7D%5Cright%29%5E%7B2%7D%7D%20%5Csqrt%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%5Cleft%28Y%7Bi%7D-%5Cmu_%7BY%7D%5Cright%29%5E%7B2%7D%7D%7D%0A&height=62&width=630)

相关系数是衡量随机变量 X 与 Y 相关程度的一种方法，相关系数的取值范围是 [-1,1]。相关系数的绝对值越大，则表明 X 与 Y 相关度越高。当 X 与 Y 线性相关时，相关系数取值为 1（正线性相关）或 -1（负线性相关）。

当 和 均为 时，，皮尔逊相关系数转化为余弦相似度

(2) 相关距离的定义

KS 距离 (Kolmogorov-Smirnov Distance)

KS Test（Kolmogorov-Smirnov）是由两位苏联数学家 A.N. Kolmogorov 和 N.V. Smirnov 提出的，用于比较样本与参考概率分布或比较两个样本的非参数检验。
以两样本为例，假设 m 个 sample 来自分布 F(x)，n 个来自 G(x)，定义 KS 统计量（KS 距离）为：

其中， 表示上确界，也就是最小上界；F(x) 和 G(x) 都是经验累积分布函数 ECDF（empirical distribution function），定义如下：

信息熵 (Information Entropy)

信息熵是衡量分布的混乱程度或分散程度的一种度量。分布越分散（或者说分布越平均），信息熵就越大；分布越有序（或者说分布越集中），信息熵就越小。
计算给定的样本集X的信息熵的公式：
%20%3D%20%5Csum%7Bi%3D1%7D%5En-p_ilog_2p_i%0A#card=math&code=Entropy%28X%29%20%3D%20%5Csum%7Bi%3D1%7D%5En-p_ilog_2p_i%0A&height=49&width=209)

n: 样本集 X 的分类数；: X 中第 i 类元素出现的概率
信息熵越大表明样本集 X 分类越分散，信息熵越小则表明样本集 X 分类越集中。当 X 中 n 个分类出现的概率一样大时（都是 1/n），信息熵取最大值 #card=math&code=log_2%28n%29&height=20&width=52)；当 X 只有一个分类时，信息熵取最小值 0。

相对熵 (Relative Entropy) 与 K-L 散度 (Kullback-Leibler Divergence)

相对熵就是 K-L 散度（Kullback-Leibler 散度），给出了两个分布之间的差异程度的量化，也就说相对熵代表的是这个两个分布的“距离”。其值越大则说明两个概率分布的差距越大；当两个分布完全相等时 K-L 散度值为 0。
K-L 散度不具有对称性；且 K-L 散度是非负的。

离散随机变量的 K-L 散度

对于离散随机变量，其概率分布 和 的 KL 散度定义为：

连续随机变量的 K-L 散度

对于连续随机变量，其概率分布 和 的 KL 散度定义为：

J-S 散度 (Jensen-Shannon Divergence)

Jensen-Shannon 散度定义于两个概率分布之上，是根据 K-L 散度构造的，同样描述了两个概率分布之间的差异，且具有对称性。

对于两个概率分布 和 ，它们的 J-S 散度定义为：

其中，概率分布 为 和 的平均值，是这两个概率分布的概率质量函数或概率密度函数的均值：

当且仅当两个概率分布相等时，即 时，

α 散度 (Alpha Divergence)

该式忘了是什么……

巴氏距离、海林格距离、K-L 散度

巴氏系数为：

海林格距离可由巴氏距离得到：

K-L 散度、海林格距离与巴氏系数的关系：

证明：

然而，巴氏距离为：

于是：

因此：

因为：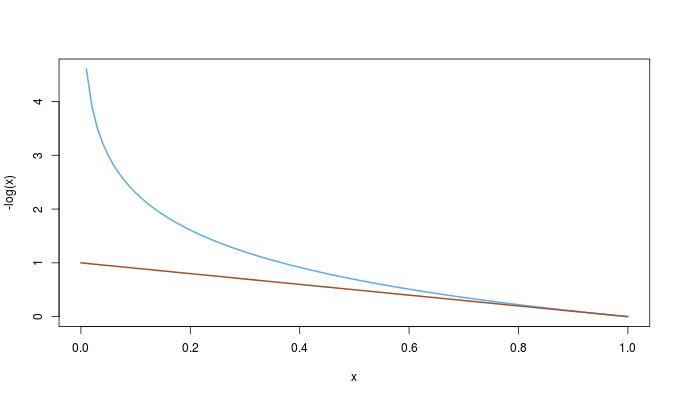


所以：

参考资料

1. 机器学习中的相似性度量：https://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html
2. 机器学习中“距离与相似度”计算汇总：https://zhuanlan.zhihu.com/p/342861735
3. 动态规划之——莱文斯坦距离和最长公共子序列：https://zhuanlan.zhihu.com/p/95592490