之前我们讨论的是回归问题,即输出是连续值,现在我们来讨论输出是离散值的分类问题
本节我们将专注于二元分类问题,即输出 y 只能取 0 和 1 两个值
逻辑回归
- 如果将线性回归模型直接应用于分类问题,会产生取值不在 0 和 1 之间的问题,所以我们引入逻辑回归模型:
- 其中:
-  被称为**逻辑函数**或 **S 型函数**,其图像如下:

- 可以看到,当  时  趋向于 1 , 当  时  趋向于 0 ,即  的值域为 (0,1),至于为什么要选择这个函数,在之后会作出解释
- 首先给出一个关于 S 型函数求导的有用性质:
确定了模型之后,我们需要找到合适的
的值
- 这里采用之前使用的最大似然法来选择参数(假设函数可以直接看作概率分布)
首先,二元分类符合伯努利分布,我们假设:
- 将上面的公式合二为一,得到:
- 假定 m 个样本之间相互独立,我们可以得到
的似然函数如下:
- 与之前类似,为了计算方便,我们使用对数似然函数来进行最大化分析:
下面要做的是使得
最大的
值,由于这里是找最大值而非最小值,所以使用梯度上升(gradient ascent)
参数的更新规则是
对于随机梯度上升(每次只考虑一个样本),求导过程如下:
- 在计算过程中使用到了 S 型函数的求导性质
- 综上所述,我们得到随机梯度上升的更新规则是:
这个公式和线性回归中梯度下降的公式表面上看是一样的,但实际上两者的
有所不同
关于更加深层次的讨论,请参看之后的 GLM 模型章节
牛顿方法
下面介绍另一种求解
的最大值的算法,称为牛顿方法
我们通过如下的几张图来理解牛顿方法:
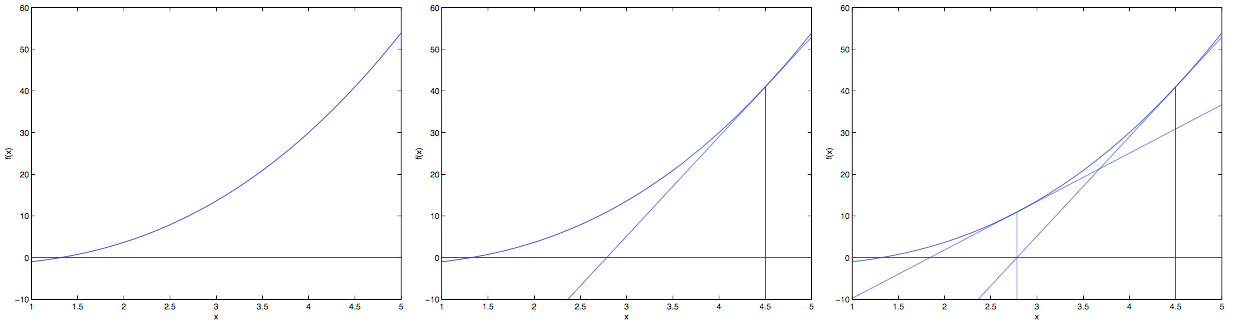
对于梯度下降,每次只是在梯度方向上下降一小步(具体速度取决于学习速率)
而牛顿方法是一直下降到导数(切线)和
轴交界的那个
。因此牛顿方法的更新规则是:
- 下面我们将牛顿方法应用于逻辑回归,我们需要找到
的最大值,即
,因此令
,我们可以得到逻辑回归的牛顿方法更新公式:
- 而对于
为向量的情况,牛顿方法的多维形式如下(又被称为牛顿-拉夫逊方法):
其中
是
对于每个
的偏导数构成的向量
是一个
的矩阵(包括截距项),称为海森矩阵,其中的每一项定义为:
和(批量)梯度下降相比,牛顿方法会带来更快的收敛速度和更少的迭代次数
- 虽然每次迭代的计算量较大,但对于参数数量不是特别大的情况,总的来说它还是更快的
将牛顿方法用于求解逻辑回归的对数似然函数最大值,也被称为费雪评分
感知器学习算法
下面介绍另一种二分类方法:感知器学习算法
感知器学习算法的假设函数为:
可以看到 g(z) 是逻辑回归的s型函数的简化形式
逻辑函数的输出是在连续的 [0,1] 区间上,而感知器直接非0则1
- 感知器学习算法的参数更新规则如下:
19世纪60年代,感知器被看作是大脑工作中独立神经元的粗糙模型
虽然直观看上去,感知器和之前所说的逻辑回归或线性回归很像,但是其实是非常不一样的算法
- 因为对于感知器学习算法,很难赋予一种有意义的概率解释,或使用最大似然估计算法来进行推导

