原文：Gillespie_algorithm 部分内容是谷歌翻译机翻…

在概率论领域，Gillespie算法（偶尔被称为Doob-Gillespie算法）可以生成一个反应率已知的随机方程组的统计学正确的结果。1945年，Joseph L. Doob等人创建了该算法，Dan Gillespie在1976年介绍了该算法，随之在他1977年的的论文里用来精确有效地模拟化学或生化系统的反应，而且只用到了有限的算力。随着计算机计算速度的提升，该算法已经在持续增长的复杂系统中被投入使用。该算法在模拟细胞内部的反应时尤为合用，因为此种情形下试剂量较少，追踪单个分子的位置和行为在计算上是可行的。数学上来说，这是一个动态蒙特卡洛方法的变种，而且与动力学蒙特卡洛方法十分相似。该算法在计算系统生物学领域被广泛使用。

历史

该算法的形成走过了几个重要阶段。1931年，Andrei Kolmogorov引入了与跳跃进行的的，时间演进的随机过程相对应的微分方程，也就是今天的Kolmogorov方程（自然科学中有一种名为大师方程的简单版本）。William Feller在1940年发现了该方程允许可能性作为结果的条件。在他的定理 I（1940年著作）中，他确定了下一次跳跃的时间是指数分布的，下一个事件的发生概率与比率成正比。这样，他建立了Kolmogorov方程与随机过程的关系。后来，Doob（1942，1945）将Feller的解法扩展到了纯粹的跳跃过程之外。该方法由David George Kendall（1950）使用曼彻斯特马克一型计算机实现，后来由Maurice S. Bartlett（1953）在他的流行病研究中使用。Gillespie（1977）通过使用物理参数以不同的方式获得了该算法。

算法思想

传统的连续和确定性生化速率方程无法准确预测细胞反应，因为它们依赖于需要数百万个分子相互作用的本体反应。通常将它们建模为一个常微分方程组。Gillespie算法则背道而驰，它允许系统中出现少量反应物的离散和随机的模拟，因为每一个反应都会被精确地模拟出来。对应于单个Gillespie模拟的轨迹表示来自概率质量函数的精确采样，该概率质量函数正是大师方程的解。

该算法的物理学基础是反应容器内分子的碰撞。它假定碰撞是频繁的，但是具有适当方向和能量的碰撞确实稀少的。因此，算法框架下的所有反应最多只会引入两个分子。涉及三个分子的反应极为罕见，并被建模为一系列的二元反应。 该算法还假定反应环境是充分混合的。

算法

最近的一篇综述（Gillespie，2007年）概述了三种不同但等效的表述： 直接法，第一反应法和第一族方法，前两种是后者的特例。直接和首次反应方法的制定集中于在所谓的“随机化学动力学的基本前提”上执行通常的蒙特卡洛反演步骤，也就是这个函数：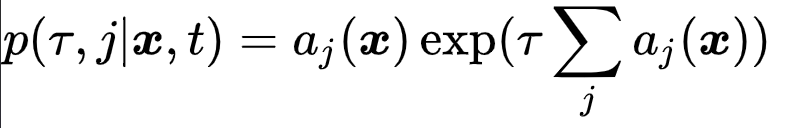

其中每一个都是一个基本反应的倾向函数，其参数是，样本数量的向量。而参数则是距离下次反应的时间（或称停留时间），参数自然就是当前时间。要描述Gillespie算法，上述表达式可以读作“概率是，给定，系统的下一次反应会在的无限时间间隔内发生，而且会被作为化学计量的第次反应。”该方程假设是一个指数分布的随机变量，并且是统计学独立的随机整数，其概率分布是，这样就为直接法和第一反应法提供了一个窗口。

因此，应用蒙特卡洛生成方法只是简单地生成两个区间为的伪随机数, 然后去计算:

并且

将这种生成方法用于停留时间和下一反应，Gillespie将直接法算法描述为：

1. 初始化时间, 系统状态
2. 系统在时间时处于状态, 计算所有的以及它们的和
3. 执行替换和, 影响下一个反应
4. 记录。返回第一步或者结束模拟。

该算法族系的计算量很大，因此存在许多修改和适应，包括下一反应方法（Gibson＆Bruck），tau-leaping以及混合技术，在该技术中，大量反应物具有确定性行为进行建模。适应性技术通常会在算法与大师方程连接时损害算法背后的理论准确性，但会为大幅度改善时间尺度提供合理的实现。该算法精确版本的计算成本由反应网络的耦合类别确定。在弱耦合网络中，受任何其他反应影响的反应数量上限是一个较小的常数。在强耦合网络中，单个反应激发理论上可以影响所有其他反应。
对于弱耦合网络，已有具有常数时间级的该类型算法版本，可以高效地模拟具有大量反应通道的系统（Slepoy Thompson Plimpton 2008）。Bratsun等人已经开发了广义Gillespie算法，该算法归功于随机生化事件具有的延迟非马尔可夫性。
由Ramaswamy等人独立开发的倾向方程（2009，2010）和Indurkhya and Beal（2010）可以构建该版本的算法，其计算成本与网络中化学样本的数量成正比，而不是与（较大的）反应数量成正比。这些公式可以减少针对弱耦合网络的恒定时间缩放的计算成本，并可以针对强耦合网络的物种数量最大程度地线性缩放。此后还有了广义Gillespie算法用于时滞反应的部分倾向变种（Ramaswamy Sbalzarini 2011）。使用部分倾向方法仅限于基本化学反应，即最多与两种不同反应物发生的反应。每个非基本化学反应都可以等价地分解为一组基本反应，但代价是网络规模呈线性增长（按反应顺序）。
考虑以下直接和第一反应法的面向对象的实现，这些方法被放在Python 3的类中：

from math import log
class SSA:
    """Container for SSAs"""
    def __init__(self, model, seed=1234):
        """Initialize container with model and pseudorandom number generator"""
        self.model = model
        self.random = Mersenne(seed=seed)
    def direct(self):
        """Indefinite generator of direct-method trajectories"""
        while True:
            while not self.model.exit():
                # evaluate weights and partition
                weights = [
                    (rxn, sto, pro(self.model))
                    for (rxn, sto, pro) in self.model.reactions
                ]
                partition = sum(w[-1] for w in weights)
                # evaluate sojourn time (MC step 1)
                sojourn = log(1.0 / self.random.floating()) / partition
                self.model["time"].append(self.model["time"][-1] + sojourn)
                # evaluate the reaction (MC step 2)
                partition = partition * self.random.floating()
                while partition >= 0.0:
                    rxn, sto, pro = weights.pop(0)
                    partition -= pro
                for species, delta in sto.items():
                    self.model[species].append(self.model[species][-1] + delta)
                self.model.curate()
            yield self.model
            self.model.reset()
    def first_reaction(self):
        """Indefinite generator of 1st-reaction trajectories"""
        while True:
            while not self.model.exit():
                # evaluate next reaction times
                times = [
                    (
                        log(
                            1.0 / self.random.floating()
                        ) / pro(self.model),
                        sto
                    )
                    for (rxn, sto, pro) in self.model.reactions
                ]
                times.sort()
                # evaluate reaction time
                self.model["time"].append(
                    self.model["time"][-1] + times[0][0]
                )
                # evaluate reaction
                for species, delta in times[0][1].items():
                    self.model[species].append(
                        self.model[species][-1] + delta
                    )
                self.model.curate()
            yield self.model
            self.model.reset()

可以看出，像所有蒙特卡洛方法一样，SSA需要种子来保证可重复性，该种子被名为Mersenne的伪随机数生成器使用。Mersenne的实现可以在Mersenne Twister一文中找到，但是像 random.random 这样的实现也是可以使用的。 direct 和 first_reaction 都是无限生成的，也就是说它们会持续地产生结果，每个结果都是对系统的完整模拟，知道这种无限循环被信号打破。
为了实际去实现这样的循环并产生一些结果进行分析，此类需要在实例化时将模型传递给它。
模型类的目的是避免将要模拟的特定过程的动力学特性与Gillespie算法的逻辑混合在一起。这个模型应该是一个字典的子类，有着 curate , exit 和 reset 的公有成员，它们分别表示：

• 确定在给定结果的每次迭代结束时哪些反应是有效的，哪些无效；
• 如果没有其他可能的反应就返回 True ；
• 在给定结果的末尾将模型哈希返回其原始值（即其初始条件）。

请看下面的在SIR示例中使用到的模型实现：

class SSAModel(dict):
    """Container for SSA model"""
    def __init__(
        self, initial_conditions, propensities, stoichiometry
    ):
        """
        Initialize model with a dictionary of initial conditions (each
        """
        super().__init__(**initial_conditions)
        self.reactions = list()
        self.excluded_reactions = list()
        for reaction,propensity in propensities.items():
            if propensity(self) == 0.0:
                self.excluded_reactions.append(
                    (
                        reaction,
                        stoichiometry[reaction],
                        propensity
                    )
                )
            else:
                self.reactions.append(
                    (
                        reaction,
                        stoichiometry[reaction],
                        propensity
                    )
                )
    def exit(self):
        """Return True to break out of trajectory"""
        # return True if no more reactions
        if len(self.reactions) == 0: return True
        # return False if there are more reactions
        else: return False
    def curate(self):
        """Validate and invalidate model reactions"""
        # evaulate possible reactions
        reactions = []
        while len(self.reactions) > 0:
            reaction = self.reactions.pop()
            if reaction[2](self) == 0:
                self.excluded_reactions.append(reaction)
            else:
                reactions.append(reaction)
        reactions.sort()
        self.reactions = reactions
        # evaluate impossible reactions
        excluded_reactions = []
        while len(self.excluded_reactions) > 0:
            reaction = self.excluded_reactions.pop()
            if reaction[2](self) > 0:
                self.reactions.append(reaction)
            else:
                excluded_reactions.append(reaction)
        excluded_reactions.sort()
        self.excluded_reactions = excluded_reactions
    def reset(self):
        """Clear the trajectory"""
        # reset species to initial conditions
        for key in self: del self[key][1:]
        # reset reactions per initial conditions
        self.curate()

示例

没有重大变化的SIR传染病模型

SIR模型是某些疾病如何通过固定规模的人群传播的经典生物学描述。 以最简单的形式，人口中有N个成员，因此每个成员在任何时刻都可能处于三种状态之一（易感，感染或恢复），并且每个这样的成员在这些状态下都不可逆转地转换，如下面的有向图所示。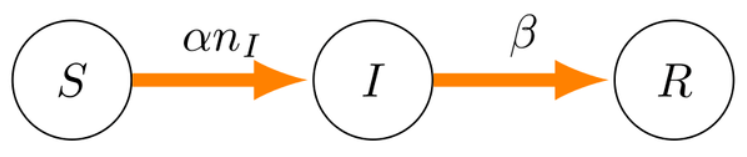

我们可以把易感者的数量设置为，感染者的数量设为，恢复者的数量为。
因此在任意时刻都有。