1. 满二叉树

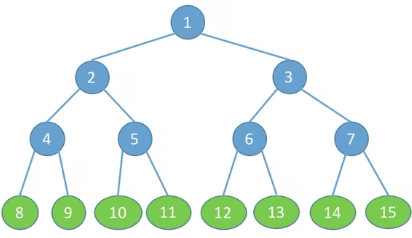
image.png
除叶子结点外，所有的结点（包括根节点）都有左右子树。
满二叉树每层的节点个数依次为：二叉树 - 图2
层数为二叉树 - 图3的满二叉树的结点总数为：二叉树 - 图4。
特点：

  • 满二叉树中的结点度数只能为0（叶子结点）或者2（非叶子节点），不能为1。
  • 如果对满二叉树中的结点从1开始按照从左到右、从上到下（层）的顺序编号，那么编号为i的结点的孩子结点（如果存在）为2i、2i+1，父节点（如果存在）为i/2（向下取整）。

2. 完全二叉树

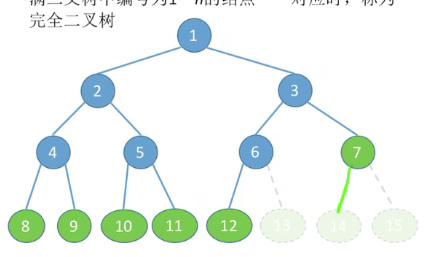
image.png
去除最后满二叉树最后几个节点。
完全二叉树中的结点与满二叉树中的结点一一对应。
特点：

  • 只有最后两层可能有叶子结点
  • 最多只有一个度为1的结点。
  • 结点i的父节点为i/2（向下取整）,子节点如果存在则为2i、2i+1。
  • 如果完全二叉树有n个结点，则i<=n/2（向下取整）的结点为分支结点，i>n/2（向下取整）的结点为叶子结点。

  • 如果某个节点只有一个孩子结点，则孩子结点一定是左孩子结点。

    判断方法

    可以借助队列以层序遍历的方式遍历树，且结点的左右子结点无论是否是空都加入到队列中，这样当第一次遇到空结点时，只需要对队列中剩余结点进行判空即可。

  • 如果队列中剩余都是空结点的，那么就是完全二叉树；

  • 否则就不是完全二叉树。

时间复杂度：O(n)，空间复杂度O(n)

  1. /**
  2.  * struct TreeNode {
  3.  *    int val;
  4.  *    struct TreeNode *left;
  5.  *    struct TreeNode *right;
  6.  * };
  7.  */
  9. class Solution {
  10. public:
  11.     bool isFBT(TreeNode* root){
  12.         // 判断一棵树是否是完全二叉树
  13.         // 用层次遍历，但是无论左右子结点是否是空，都加入到队列中
  14.         // 当一次遇到空结点时，队列中的所有现有节点都必须是空，则是完全二叉树，否则就不是
  15.         queue<TreeNode*> nodeQueue;
  16.         nodeQueue.push(root);
  17.         while(!nodeQueue.empty()){
  18.             TreeNode* front = nodeQueue.front();
  19.             nodeQueue.pop();
  21.             if(front==nullptr){
  22.                 while(!nodeQueue.empty()){
  23.                     if(nodeQueue.front() == nullptr){
  24.                         nodeQueue.pop();
  25.                     }
  26.                     else{
  27.                         return false;
  28.                     }
  29.                 }
  30.                 return true;
  31.             }
  33.             nodeQueue.push(front->left);
  34.             nodeQueue.push(front->right);
  35.         }
  36.         return true;
  37.     }
  38. };

3. 二叉排序树BST（二分查找的比较过程）

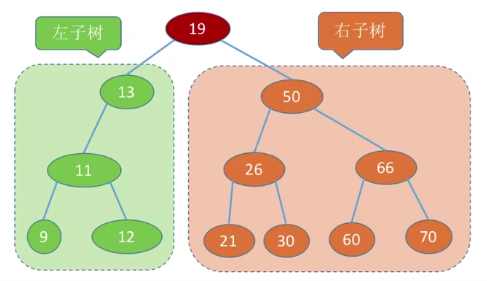
image.png
对二叉树的每个节点K，如果：

  • 左孩子节点存在，则左子树上结点的值（所有值）小于结点K的值；
  • 右孩子结点存在，则右子树上结点的值（所有值）大于结点K的值；

在已有的二叉排序树上增加节点：一层一层地比较子树根节点的值，比子树根节点值小，往左子树上找，否则，往右子树上找，直至到达叶节点，比叶子结点小，插到左子树上，否则插到右子树上。

判断方法

对树进行中序遍历，将访问到的结点的值保存到数组中，然后对数组进行升序判断。
时间复杂度O(n)，空间复杂度O(n)。

  1. /**
  2.  * struct TreeNode {
  3.  *    int val;
  4.  *    struct TreeNode *left;
  5.  *    struct TreeNode *right;
  6.  * };
  7.  */
  9. class Solution {
  10. public:
  11.     bool isBST(TreeNode* root){
  12.         // 判断是否是二叉搜索树
  13.         vector<int> midSeq;
  14.         midSearch(root, midSeq);
  15.         if(midSeq.size() <= 1){
  16.             return true;
  17.         }
  18.         for(int i=1; i<midSeq.size(); i++){
  19.             if(midSeq[i] < midSeq[i-1]){
  20.                 return false;
  21.             }
  22.         }
  23.         return true;
  24.     }
  26.     void midTravel(TreeNode* root, vector<int>& midSeq){
  27.         if(root==nullptr){
  28.             return;
  29.         }
  30.         if(root->left){
  31.             midTravel(root->left, midSeq);
  32.         }
  33.         midSeq.push_back(root->val);
  34.         if(root->right){
  35.             midTravel(root->right, midSeq);
  36.         }
  37.     }
  38. };

4. 平衡二叉树

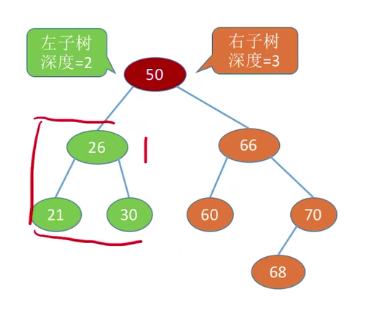
image.png
对二叉树上的每个节点来说，其左子树与右子树的深度差不超过1。
平衡的二叉排序树能有效提高查找效率。

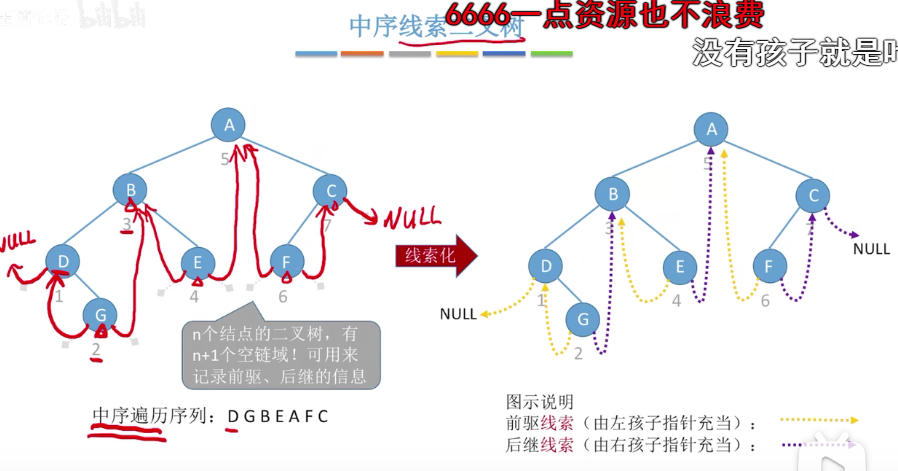
5.线索二叉树

具有n个结点的二叉树有n+1个空闲指针，按遍历顺序对结点定义前驱和后继，可得到线索二叉树，由此方便得到结点的后序结点或前驱结点。

  • 先序线索二叉树
  • 中序线索二叉树
  • 后序线索二叉树
  • 层序线索二叉树

image.png