1. 模式串匹配

  1. 题目：给出两个字符串，分别是模式串P和目标串T，
  2. 判断模式串和目标串是否匹配，匹配输出 1，不匹配输出 0。
  3. 模式串中‘？’可以匹配目标串中的任何字符，
  4. 模式串中的 ’*’可以匹配目标串中的任何长度的串，
  5. 模式串的其它字符必须和目标串的字符匹配。
  7. 输入描述:
  8. 输入第一行包含一个字符串p， (1 ≤ |p| ≤ 20).
  9. 输入第二行包含一个字符串t， (1 ≤ |t| ≤ 20).
  10. 输出描述:
  11. 输出仅包含0和1的整数，0表示p和t不匹配，1表示p和t匹配。
  1. #include<iostream>
  2. #include<string>
  3. #include<vector>
  4. using namespace std;
  5. //算法思想：dp[i][j]为s[1...i]与t[1...j]是否匹配。
  6. int main()
  7. {
  8.     string s1;
  9.     string s2;
  10.     while (cin >> s2 >> s1)
  11.     {
  12.         int m = s1.size(); int n = s2.size();
  13.         vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, 0));
  14.         dp[0][0] = 1;
  15.         for (int i = 1; i <= n; i++)
  16.             dp[0][i] = dp[0][i - 1] && s2[i - 1] == '*';
  17.         for (int i = 1; i <= m; i++)
  18.         {
  19.             for (int j = 1; j <= n; j++)
  20.             {
  21.                 if (s1[i - 1] == s2[j - 1] || s2[j - 1] == '?')
  22.                     dp[i][j] = dp[i - 1][j - 1];
  23.                 if (s2[j - 1] == '*')
  24.                     dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
  25.             }
  26.         }
  27.         cout << dp[m][n] << endl;
  28.     }
  29.     return 0;
  30. }

2. 完全背包—组合——零钱兑换II

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
输入: amount = 10, coins = [10]
输出: 1

算法思想：（类比0/1背包问题）
因为这是个组合问题，我们不关心硬币使用的顺序，而是硬币有没有被用到。是否使用第k个硬币受到之前情况的影响。
状态转移方程如下
if 金额数大于硬币
DP[k][i] = DP[k-1][i] + DP[k][i-k]
else
DP[k][i] = DP[k-1][i]

  1. class Solution {
  2. public:
  3.     int change(int amount, vector<int>& coins) {
  4.         int K = coins.size() + 1;
  5.         int I = amount + 1;
  6.         int DP[K][I];
  7.         //初始化数组
  8.         for (int k = 0; k < K; k++){
  9.             for (int i = 0; i < I; i++){
  10.                 DP[k][i] = 0;
  11.             }
  12.         }
  13.         //初始化基本状态
  14.         for (int k = 0; k < coins.size() + 1; k++){
  15.             DP[k][0] = 1;
  16.         }
  17.         //k,i循环可互换
  18.         for (int k = 1; k <= coins.size() ; k++){ 
  19.             for (int i = 1; i <= amount; i++){  
  20.                 if ( i >= coins[k-1]) {
  21.                     DP[k][i] = DP[k][i-coins[k-1]] + DP[k-1][i]; 
  22.                 } else{
  23.                     DP[k][i] = DP[k-1][i];
  24.                 }
  25.             }
  26.         }
  27.         return DP[coins.size()][amount];
  28.     }
  29. };
  32. 进阶：
  33. 之前爬楼梯问题中，我们将一维数组降维成点。这里问题能不能也试着降低一个维度，只用一个数组进行表示呢？
  34. 这个时候，我们就需要重新定义我们的子问题了。
  35. 此时的子问题是，对于硬币从0到k，我们必须使用第k个硬币（前k个硬币）的时候，当前金额的组合数。
  36. 因此状态数组DP[i]表示的是对于第k个硬币能凑的组合数
  37. 状态转移方程如下：
  38.     DP[i] = DP[i] + DP[i-coins[k]] 
  39. class Solution {
  40. public:
  41.     int change(int amount, vector<int>& coins) {
  42.         int dp[amount+1];
  43.         memset(dp, 0, sizeof(dp)); //初始化数组为0
  44.         dp[0] = 1;
  45.         for (int coin : coins){ //枚举硬币
  46.             for (int i = 1; i <= amount; i++){ //枚举金额
  47.                 if (i < coin) continue; // coin不能大于amount
  48.                 dp[i] += dp[i-coin];
  49.             }
  50.         }
  51.         return dp[amount];
  52.     }
  53. };

3. 0/1背包——分割等和子集

题目：
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

算法思想：
3`UNABGD4]2SU}$%X5]YZ2S.png

  1. class Solution {
  2. public:
  3.     bool canPartition(vector<int>& nums) {
  4.         int n = nums.size();
  5.         if (n < 2) {
  6.             return false;
  7.         }
  8.         int sum = accumulate(nums.begin(), nums.end(), 0);
  9.         int maxNum = *max_element(nums.begin(), nums.end());
  10.         if (sum & 1) {
  11.             return false;
  12.         }
  13.         int target = sum / 2;
  14.         if (maxNum > target) {
  15.             return false;
  16.         }
  17.         vector<vector<int>> dp(n, vector<int>(target + 1, 0));
  18.         for (int i = 0; i < n; i++) {
  19.             dp[i][0] = true;
  20.         }
  21.         dp[0][nums[0]] = true;
  22.         for (int i = 1; i < n; i++) {
  23.             int num = nums[i];
  24.             for (int j = 1; j <= target; j++) {
  25.                 if (j >= num) {
  26.                     dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
  27.                 } else {
  28.                     dp[i][j] = dp[i - 1][j];
  29.                 }
  30.             }
  31.         }
  32.         return dp[n - 1][target];
  33.     }
  34. };
  36. 改进：
  37. vector<int> dp(target + 1, 0);
  38. dp[0] = true;
  39. for (int i = 0; i < n; i++) {
  40.     int num = nums[i];
  41.     for (int j = target; j >= num; --j) {
  42.         dp[j] |= dp[j - num];
  43.     }
  44. }
  45. return dp[target];

4. 0/1背包——最后一块石头的重量 II

题目：
有一堆石头，每块石头的重量都是正整数。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。
示例：
输入：[2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

算法思想：同题3类似，求容量为target = sum /2的最大背包装载量。

  1. class Solution {
  2. public:
  3.     int lastStoneWeightII(vector<int>& stones) {
  4.         vector<int> dp(15001, 0);
  5.         int sum = 0;
  6.         for (int i = 0; i < stones.size(); i++) sum += stones[i];
  7.         int target = sum / 2;
  8.         for (int i = 0; i < stones.size(); i++) { // 遍历物品
  9.             for (int j = target; j >= stones[i]; j--) { // 遍历背包
  10.                 dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
  11.             }
  12.         }
  13.         return (sum - dp[target]) - dp[target];
  14.     }
  15. };

5. 预测赢家

题目：
给定一个表示分数的非负整数数组。 玩家 1 从数组任意一端拿取一个分数，随后玩家 2 继续从剩余数组任意一端拿取分数，然后玩家 1 拿，…… 。每次一个玩家只能拿取一个分数，分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。
给定一个表示分数的数组，预测玩家1是否会成为赢家。你可以假设每个玩家的玩法都会使他的分数最大化。（每个玩家都能看到所有的数字）

示例 1：
输入：[1, 5, 2]
输出：False
解释：一开始，玩家1可以从1和2中进行选择。
如果他选择 2（或者 1 ），那么玩家 2 可以从 1（或者 2 ）和 5 中进行选择。如果玩家 2 选择了 5 ，那么玩家 1 则只剩下 1（或者 2 ）可选。
所以，玩家 1 的最终分数为 1 + 2 = 3，而玩家 2 为 5 。
因此，玩家 1 永远不会成为赢家，返回 False 。

法一：回溯法

  1. class Solution {
  2.     public boolean PredictTheWinner(int[] nums) {
  3.         return total(nums, 0, nums.length - 1, 1) >= 0;
  4.     }
  6.     public int total(int[] nums, int start, int end, int turn) {
  7.         if (start == end) {
  8.             return nums[start] * turn;
  9.         }
  10.         int scoreStart = nums[start] * turn + total(nums, start + 1, end, -turn);
  11.         int scoreEnd = nums[end] * turn + total(nums, start, end - 1, -turn);
  12.         return Math.max(scoreStart * turn, scoreEnd * turn) * turn;
  13.            # 此处时关键：玩家一会选择当前total最大的选择，而玩家二会选择当前total小的选择
  14.     }
  15. }
  17. //时间复杂度：O(2^n)，其中 nn 是数组的长度。
  18. //空间复杂度：O(n)，其中 nn 是数组的长度。空间复杂度取决于递归使用的栈空间。

法二：动态规划

  1. //dp[i][j] 表示当数组剩下的部分为下标 ii 到下标 jj 时，当前玩家与另一个玩家的分数之差的最大值，
  2. //注意当前玩家不一定是先手。
  4. class Solution {
  5. public:
  6.     bool PredictTheWinner(vector<int>& nums) {
  7.         int length = nums.size();
  8.         auto dp = vector<vector<int>> (length, vector<int>(length));
  9.         for (int i = 0; i < length; i++) {
  10.             dp[i][i] = nums[i];
  11.         }
  12.         for (int i = length - 2; i >= 0; i--) { //
  13.             for (int j = i + 1; j < length; j++) {
  14.                 dp[i][j] = max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1]);
  15.             }
  16.         }
  17.         return dp[0][length - 1] >= 0;
  18.     }
  19. };
  21. 优化：
  22. auto dp = vector<int>(length);
  24. dp[j] = max(nums[i] - dp[j], nums[j] - dp[j - 1]);
  26. return dp[length - 1] >= 0;

6. 预测赢家2——（偶数堆）石子游戏

题目：
亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。 每回合，玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。
假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

示例：
输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

  1. 法一：同预测赢家问题（动态规划）
  2. class Solution {
  3. public:
  4.     bool stoneGame(vector<int>& piles) {
  5.         int length = piles.size();
  6.         auto dp = vector<vector<int>> (length, vector<int>(length));
  7.         for (int i = 0; i < length; i++) {
  8.             dp[i][i] = piles[i];
  9.         }
  10.         for (int i = length - 2; i >= 0; i--) { // 由短到长的新写法（其他写法：len = 2->len,i = 0->n）
  11.             for (int j = i + 1; j < length; j++) {
  12.                 dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
  13.             }
  14.         }
  15.         return dp[0][length - 1] >= 0;
  16.     }
  17. };
  19. 法二：数学方法分析
  20. 假设有n堆石子，n是偶数，则每堆石子的下标从 0 到 n-1。根据下标将 n 堆石子分成两组，
  21. 每组有n/2堆石子，下标为偶数的石子堆属于第一组，下标为奇数的石子堆属于第二组。
  23. 初始时，行的开始处的石子堆位于下标 0，属于第一组，
  24. 行的结束处的石子堆位于下标 n-1，属于第二组，因此作为先手的
  25. Alex 可以自由选择取走第一组的一堆石子或者第二组的一堆石子。
  26. 如果Alex 取走第一组的一堆石子，则剩下的部分在行的开始处和结束处的石子堆都属于第二组，
  27. 因此Lee 只能取走第二组的一堆石子。同理...
  28. 所以，如果作为先手的Alex 可以在第一次取走石子时就决定取走哪一组的石子，并全程取走同一组的石子，
  29. 就能得到唯一的比赛结果。故先手Alex必胜。
  31. class Solution {
  32. public:
  33.     bool stoneGame(vector<int>& piles) {
  34.         return true;
  35.     }
  36. };

7. 最长递增子序列

题目：
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4

算法：定义dp[i]为以nums[i]结尾的最长公共子序列的长度。
WU}B[MZ{1A5(R$`]M45_ZDX.png

  1. class Solution {
  2. public:
  3.     int lengthOfLIS(vector<int>& nums) {
  4.         int n=nums.size(),maxn = 0;;
  5.         vector<int> dp(n);
  6.         for(int i=0;i<n;i++){
  7.             dp[i] = 1;
  8.             for(int j=i-1;j>=0;j--){
  9.                 if(nums[j]>= nums[i]) continue;
  10.                 dp[i] = max(dp[i],dp[j]+1);
  11.             }
  12.         }
  13.         return *max_element(dp.begin(), dp.end());
  14.     }
  15.     /* 错解：单调递增栈
  16.     int lengthOfLIS(vector<int>& nums) {
  17.         stack<int> ascendNums;
  18.         int maxlen=1;
  19.         ascendNums.push(nums[0]);
  20.         for(int i=1;i<nums.size();i++){
  21.             while(!ascendNums.empty()&&nums[i]<=ascendNums.top()){
  22.                 ascendNums.pop();
  23.             }
  24.             ascendNums.push(nums[i]);
  26.             if(ascendNums.size() > maxlen){
  27.                 maxlen = ascendNums.size();
  28.             }
  29.         }
  30.         return maxlen;
  31.     }
  32.     */
  33. };

变体：最长嵌套盒子

题目：
有n个矩形，每个矩形可以用a,b来描述，表示长和宽。矩形X(a,b)可以嵌套在矩形Y(c,d)中当且仅当a输入描述:
第一行是一个正正数N(0每组测试数据的第一行是一个正正数n，表示该组测试数据中含有矩形的个数(n<=1000)
随后的n行，每行有两个数a,b(0输出描述:
每组测试数据都输出一个数，表示最多符合条件的矩形数目，每组输出占一行
样例输入:
1
10
1 2
2 4
5 8
6 10
7 9
3 1
5 8
12 10
9 7
2 2
样例输出:
5
算法：
先按宽排序，再按高来挑选最长递增子序列。

  1. #include<iostream>
  2. #include<cstring>
  3. #include<cstdio> 
  4. #include<algorithm>
  5. using namespace std;
  7. struct node{
  8.     int x,y;
  9. }p[100009];
  11. int dp[100009];
  13. bool cmp(node a,node b)
  14. {
  15.     if(a.x == b.x)
  16.     {
  17.         return a.y<b.y;
  18.     }
  19.     return a.x<b.x;
  20. }
  22. int main()
  23. {
  24.     int n;
  25.     scanf("%d",&n);
  26.     while(n--)
  27.     {
  28.         int n1;
  29.         memset(dp,0,sizeof(dp));
  30.         memset(p,0,sizeof(p));
  31.         scanf("%d",&n1);int rr = 0,k1=0,k2 = 0;
  32.         for(int i=0;i<n1;++i)
  33.         {
  34.             scanf("%d%d",&k1,&k2);
  35.             p[rr].x = k1;p[rr].y = k2;rr++;
  36.             p[rr].x = k2;p[rr].y = k1;rr++;//把两种状态模拟一下
  37.         }
  38.         sort(p,p+rr,cmp);int r=0;int max1 = 1;
  39.         //套最长上升子序列模板
  40.         for(int i = 0;i < rr;++i)
  41.         {
  42.             dp[i] = 1;
  43.             for(int j = 0;j < i;++j)
  44.             {
  45.                 if(p[i].y>p[j].y && p[i].x>p[j].x)
  46.                 {
  47.                     dp[i] = max(dp[i],dp[j]+1);    
  48.                 }
  49.             }
  50.             max1 = max(max1,dp[i]);
  51.         }
  53.         printf("%d\n",max1);
  54.     }
  55.     return 0;
  56. }

8. 买卖股票【状态】

多次买卖

题目：可以多次买卖，买一个新股票时手里不能留有股票。求最大利润。
方法：求所有升序和。

  1. class Solution {
  2. public:
  3.     int maxProfit(vector<int>& prices) {
  4.         int n = prices.size();
  5.         int sum = 0;
  6.         for(int i=1; i<n;i++){
  7.             if(prices[i] - prices[i-1] > 0){
  8.                 sum += prices[i] - prices[i-1];
  9.             }
  10.         }
  11.         return sum;
  12.     }
  13. };

两次买卖——状态+动态规划

题目：可以进行最多两次买卖，买一个新股票时手里不能留有股票（可以先卖再买）
算法：
由于我们最多可以完成两笔交易，因此在任意一天结束之后，我们会处于以下五个状态中的一种：

  • 未进行过任何操作；
  • 只进行过一次买操作；
  • 进行了一次买操作和一次卖操作，即完成了一笔交易；
  • 在完成了一笔交易的前提下，进行了第二次买操作；
  • 完成了全部两笔交易。

动态规划：转移方程
![S3(U6%N14`BO50CT97XXP3.png

  2. class Solution {
  3. public:
  4.     int maxProfit(vector<int>& prices) {
  5.         int n = prices.size();
  6.         int buy1 = -prices[0], sell1 = 0;
  7.         int buy2 = -prices[0], sell2 = 0;
  8.         for (int i = 1; i < n; ++i) {
  9.             buy1 = max(buy1, -prices[i]);
  10.             sell1 = max(sell1, buy1 + prices[i]);
  11.             buy2 = max(buy2, sell1 - prices[i]);
  12.             sell2 = max(sell2, buy2 + prices[i]);
  13.         }
  14.         return sell2;
  15.     }
  16. };

多次买卖含冷冻期——状态+动态规划

题目：
定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

算法：
用 f[i] 表示第 i 天结束之后的「累计最大收益」
此时会有三种不同的状态：

  • 我们目前持有一支股票，尚未卖出，对应的「累计最大收益」记为 f[i][0]；
  • 我们目前不持有任何股票，因为今天刚卖出，明天将处于冷冻期中，对应的「累计最大收益」记为 f[i][1}；
  • 我们目前不持有任何股票，对应的「累计最大收益」记为 f[i][2]。

转移方程：
MAAH_YTA6S[FJZ3LHV~7{@4.png](https://cdn.nlark.com/yuque/0/2021/png/263367/1615774964563-d56044a9-7213-4b90-bde0-eede20467d63.png#height=43&id=JWF9r&margin=%5Bobject%20Object%5D&name=MAAH_YTA6S%5BFJZ3LHV~7%7B%404.png&originHeight=62&originWidth=543&originalType=binary&size=6425&status=done&style=none&width=373)<br />![HJ06A6S{H6]V%KA$(7N{SJE.png
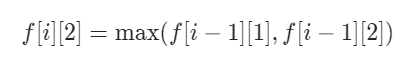
J80T0@)42@RSCT731H{ZVGP.png

  1. class Solution {
  2. public:
  3.     int maxProfit(vector<int>& prices) {
  4.         if (prices.empty()) {
  5.             return 0;
  6.         }
  8.         int n = prices.size();
  9.         // f[i][0]: 手上持有股票的最大收益
  10.         // f[i][1]: 手上不持有股票，并且处于冷冻期中的累计最大收益
  11.         // f[i][2]: 手上不持有股票，并且不在冷冻期中的累计最大收益
  12.         vector<vector<int>> f(n, vector<int>(3));
  13.         f[0][0] = -prices[0];
  14.         for (int i = 1; i < n; ++i) {
  15.             f[i][0] = max(f[i - 1][0], f[i - 1][2] - prices[i]);
  16.             f[i][1] = f[i - 1][0] + prices[i];
  17.             f[i][2] = max(f[i - 1][1], f[i - 1][2]);
  18.         }
  19.         return max(f[n - 1][1], f[n - 1][2]);
  20.     }
  21. };
  23. 空间优化：
  24.     {
  25.         int f0 = -prices[0];
  26.         int f1 = 0;
  27.         int f2 = 0;
  28.         for (int i = 1; i < n; ++i) {
  29.             int newf0 = max(f0, f2 - prices[i]);
  30.             int newf1 = f0 + prices[i];
  31.             int newf2 = max(f1, f2);
  32.             f0 = newf0;
  33.             f1 = newf1;
  34.             f2 = newf2;
  35.         }
  37.         return max(f1, f2);
  38.     }

多次买卖含手续费

题目：
给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1:
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

法一：动态规划+状态
(注意此题和上一题的区别，上一题由于冷冻期的存在，买股票的状态只能从非冷冻期的无股票状态买；而本题买股票的状态直接从无股票状态买，即上次一刚刚卖出我本次也可以买，故只需要两状态)

  1. class Solution {
  2. public:
  3.     int maxProfit(vector<int>& prices, int fee) {
  4.         int n=prices.size();
  5.         int f1 = -prices[0];//已买了一只股票
  6.         int f2 = 0;//本次手上没有股票
  7.         for(int i=1;i<n;i++){
  8.             int nextf1 = max(f1,f2-prices[i]);
  9.             int nextf2 = max(f2,f1+prices[i]-fee);
  10.             f1 = nextf1;
  11.             f2 = nextf2;
  12.         }
  13.         return f2;
  14.     }
  15. };

法二：贪心（将手续费算在买股票时支出）

  1. class Solution {
  2. public:
  3.     int maxProfit(vector<int>& prices, int fee) {
  4.         int n = prices.size();
  5.         int buy = prices[0] + fee;
  6.         int profit = 0;
  7.         for (int i = 1; i < n; ++i) {
  8.             if (prices[i] + fee < buy) {
  9.                 buy = prices[i] + fee;
  10.             }
  11.             else if (prices[i] > buy) {
  12.                 profit += prices[i] - buy;
  13.                 buy = prices[i]; //提供反悔机会
  14.             }
  15.         }
  16.         return profit;
  17.     }
  18. };