1. K个一组反转链表
2. 反转链表
3. 合并多个链表&优先队列
- 优先队列
- 题目
4. 树——树形体育场紧急疏散
有向树（并查集）—— 冗余连接2
5. 图——破解保险箱（欧拉图）
6. 图（拓扑排序）
- 课程表1
- 课程表2
8.判断二部图
9.二叉树
- 二叉树的中序遍历非递归写法
- 计算完全二叉树的节点数量

1. K个一组反转链表

题目：给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。
k 是一个正整数，它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。
示例：
给你这个链表：1->2->3->4->5
当 k = 2 时，应当返回: 2->1->4->3->5
当 k = 3 时，应当返回: 3->2->1->4->5

class Solution {
public:
    // 翻转一个子链表，并且返回新的头与尾
    pair<ListNode*, ListNode*> myReverse(ListNode* head, ListNode* tail) {
        ListNode* newhead = tail->next;
        ListNode* p = head;
        while (newhead != tail) {
            ListNode* nex = p->next;
            //“无”头节点的头插法方式
            p->next = newhead;
            newhead = p;
            p = nex;
        }
        return {tail, head};
    }
    ListNode* reverseKGroup(ListNode* head, int k) {
        //建立空节点
        ListNode* hair = new ListNode(0);
        hair->next = head;
        ListNode* pre = hair;
        while (head) {
            ListNode* tail = pre;
            // 查看剩余部分长度是否大于等于 k
            for (int i = 0; i < k; ++i) {
                tail = tail->next;
                if (!tail) {
                    return hair->next;
                }
            }
            // 这里是 C++17 的写法，也可以写成
            // pair<ListNode*, ListNode*> result = myReverse(head, tail);
            // head = result.first;
            // tail = result.second;
            tie(head, tail) = myReverse(head, tail);
            // 把子链表重新接回原链表
            pre->next = head;
            pre = tail;
            head = tail->next;
        }
        return hair->next;
    }
};
//mysolution:
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(!head) return NULL;
        ListNode *nullHead = new ListNode(0,head);
        ListNode *p = head,*p1=p->next,*p2, *pre, *p0 = nullHead,*q;
        int kt;
        while(p){
            kt=k;
            p2 = getNextP(p,kt);
            if(kt) return nullHead->next;
            p1 = p->next;
            pre = p;
            p->next = p2;
            for(int i=0;i<k-1;i++){
                q = p1->next;
                p1->next = pre;
                pre = p1;
                p1 = q;
            }
            p0->next = pre;
            p0 = p;
            p=p2;
        }
        return nullHead->next;
    }
    ListNode *getNextP(ListNode *p, int &k){
        int kk = k;
        for(int i=0;i<kk;i++){
            p=p->next;
            k--;
            if(!p) return NULL;
        }
        return p;
    }
};

2. 反转链表

题目：反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

法一：头插法
ListNode* reverseList(ListNode* head) {
    if(!head) return head;
    ListNode *p=head->next,*q;
    head->next = NULL;
    while(p){
        q = p->next;
        p->next = head;
            head = p;
        p = q;
    }
    return head;
}

法二：一般迭代，记录前后指针
ListNode* reverseList(ListNode* head) {
    ListNode *prev = NULL;
       ListNode *curr = head;
    while (curr != NULL) {
        ListNode *nextTemp = curr->next;
        curr->next = prev;
        prev = curr;
        curr = nextTemp;
      }
    return prev;
}

3. 合并多个链表&优先队列

优先队列

优先队列为特殊的队列，内部会自动按照关键字以堆排的方式进行排序

# 基本定义
//大顶堆，升序队列
priority_queue <int,vector<int>,greater<int> > q;
//小顶堆，降序队列
priority_queue <int,vector<int>,less<int> >q;
# 自定义优先级
#include <iostream>
#include <queue>
using namespace std;
//方法1
struct tmp1 //运算符重载<
{
    int x;
    tmp1(int a) {x = a;}
    bool operator<(const tmp1& a) const
    {
        return x < a.x; //小顶堆，队列按照从大到小排列
    }
};
//方法2
struct tmp2 //重写仿函数
{
    bool operator() (tmp1 a, tmp1 b) 
    {
        return a.x < b.x; //小顶堆，队列按照从大到小排列
    }
};
int main() 
{
    tmp1 a(1);
    tmp1 b(2);
    tmp1 c(3);
    priority_queue<tmp1> d;
    d.push(b);
    d.push(c);
    d.push(a);
    while (!d.empty()) 
    {
        cout << d.top().x << '\n';
        d.pop();
    }
    cout << endl;
    priority_queue<tmp1, vector<tmp1>, tmp2> f;
    f.push(c);
    f.push(b);
    f.push(a);
    while (!f.empty()) 
    {
        cout << f.top().x << '\n';
        f.pop();
    }
}

题目

题目：给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。
示例 1：
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

class Solution {
public:
    struct Status {
        int val;
        ListNode *ptr;
        bool operator < (const Status &rhs) const {
            return val > rhs.val;
        }
    };
    priority_queue <Status> q;
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        for (auto node: lists) {
            if (node) q.push({node->val, node});
        }
        ListNode head, *tail = &head;
        while (!q.empty()) {
            auto f = q.top(); q.pop();
            tail->next = f.ptr; 
            tail = tail->next;
            if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
        }
        return head.next;
    }
};

4. 树——树形体育场紧急疏散

题目：体育场突然着火了，现场需要紧急疏散，但是过道真的是太窄了，同时只能容许一个人通过。现在知道了体育场的所有座位分布，座位分布图是一棵树，已知每个座位上都坐了一个人，安全出口在树的根部，也就是1号结点的位置上。其他节点上的人每秒都能向树根部前进一个结点，但是除了安全出口以外，没有任何一个结点可以同时容纳两个及以上的人，这就需要一种策略，来使得人群尽快疏散，问在采取最优策略的情况下，体育场最快可以在多长时间内疏散完成。
输入描述:
第一行包含一个正整数n，即树的结点数量（1<=n<=100000）。接下来有n-1行，每行有两个正整数x，y，表示在x和y结点之间存在一条边。(1<=x，y<=n)
输出描述:
输出仅包含一个正整数，表示所需要的最短时间

示例1：
输入
6
2 1
3 2
4 3
5 2
6 1
输出
4
算法思想：
(1) 找根节点的最大子树（注意：此树是一般树，不是二叉树）
(2) 使用邻接表建树（用vector + list），再对次根节点依次广度优先遍历。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int m;cin >> m;
    vector<list<int>> vec(m, list<int>());
    int x,y,i=m-1;
    //创建邻接表
    while(i--)
    {
        cin >>x >>y;
        vec[x-1].push_back(y-1);
        vec[y-1].push_back(x-1);
    }
    queue<int> que;
    map<int, int> mac;
    vector<bool> vis(m, false);
    vector<int> subNode;
    vis[0] = true;
    int res = 0;
    //得到次子节点
    for(auto it = vec[0].begin();it!=vec[0].end();it++)
    {
        subNode.push_back(*it);
        vis[*it] = true;
    }
    //遍历次子节点分别求子树节点个数
    for(int i = 0; i < subNode.size();i++)
    {
        que.push(subNode[i]);
        int num = 0;
        while(!que.empty())
        {
            int tem = que.front();
            num++;
            vis[tem] = true;
            for(auto it = vec[tem].begin(); it != vec[tem].end(); it++)
            {
                if(!vis[*it])
                {
                    que.push(*it);
                }
            }
            que.pop();
        }
        res = res < num ? num : res;
    }
    cout << res << endl;
    return 0;
}

有向树（并查集）—— 冗余连接2

题目：
在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。
输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。每个元素是一对 [ui, vi]，用以表示有向图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。
返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：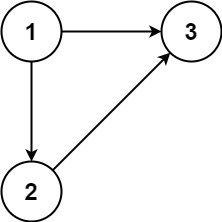
链表&图&树 - 图1

输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

算法：
分析：树中的每个节点都有一个父节点，除了根节点没有父节点。在多了一条附加的边之后，可能有以下两种情况：

附加的边指向根节点，则包括根节点在内的每个节点都有一个父节点，此时图中一定有环路；
附加的边指向非根节点，则恰好有一个节点（即被附加的边指向的节点）有两个父节点，此时图中可能有环路也可能没有环路。

解决：
使用并查集依次按边合并集合，若子节点已经有父节点，则冲突；
若子节点和父节点祖先已经相同，则有环。

struct UnionFind {
    vector <int> ancestor;
    UnionFind(int n) {
        ancestor.resize(n);
        for (int i = 0; i < n; ++i) {
            ancestor[i] = i;
        }
    }
    int find(int index) {
        return index == ancestor[index] ? index : ancestor[index] = find(ancestor[index]);
    }
    void merge(int u, int v) {
        ancestor[find(u)] = find(v);//或ancestor[find(v)] = find(u);
    }
};
class Solution {
public:
    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int nodesCount = edges.size();
        UnionFind uf = UnionFind(nodesCount + 1);
        auto parent = vector<int>(nodesCount + 1);
        for (int i = 1; i <= nodesCount; ++i) {
            parent[i] = i;
        }
        int conflict = -1;
        int cycle = -1;
        for (int i = 0; i < nodesCount; ++i) {
            auto edge = edges[i];
            int node1 = edge[0], node2 = edge[1];
            if (parent[node2] != node2) {
                conflict = i;
            } else {
                parent[node2] = node1;
                if (uf.find(node1) == uf.find(node2)) {
                    cycle = i;
                } else {
                    uf.merge(node1, node2);
                }
            }
        }
        if (conflict < 0) {
            auto redundant = vector<int> {edges[cycle][0], edges[cycle][1]};
            return redundant;
        } else {
            auto conflictEdge = edges[conflict];
            if (cycle >= 0) {
                auto redundant = vector<int> {parent[conflictEdge[1]], conflictEdge[1]};
                return redundant;
            } else {
                auto redundant = vector<int> {conflictEdge[0], conflictEdge[1]};
                return redundant;
            }
        }
    }
};

5. 图——破解保险箱（欧拉图）

题目：
有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位是 k 位序列 0, 1, …, k-1 中的一个。
你可以随意输入密码，保险箱会自动记住最后 n 位输入，如果匹配，则能够打开保险箱。
举个例子，假设密码是 “345”，你可以输入 “012345” 来打开它，只是你输入了 6 个字符.
请返回一个能打开保险箱的最短字符串。

示例1:
输入: n = 1, k = 2
输出: “01”
说明: “10”也可以打开保险箱。

示例2:
输入: n = 2, k = 2
输出: “00110”
说明: “01100”, “10011”, “11001” 也能打开保险箱。

提示：
n 的范围是 [1, 4]。
k 的范围是 [1, 10]。
k^n 最大可能为 4096。

算法：
在一个欧拉图中找出欧拉回路
9I[O71ZF0MB[8XWA4AQF$]X.png

class Solution {
private:
    unordered_set<int> seen;
    string ans;
    int highest;
    int k;
public:
    void dfs(int node) {
        for (int x = 0; x < k; ++x) {
            int nei = node * 10 + x;
            if (!seen.count(nei)) {
                seen.insert(nei);
                dfs(nei % highest);
                ans += (x + '0');
            }
        }
    }
    string crackSafe(int n, int k) {
        highest = pow(10, n - 1);
        this->k = k;
        dfs(0);
        ans += string(n - 1, '0');
        //reverse(ans.begin(),ans.end());
        return ans;
    }
};

6. 图（拓扑排序）

课程表1

题目：
你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。
例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。
示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

算法：
深度优先遍历结合栈。（emmm，直接用课程表2的拓扑排序方法不香吗）
每个元素有三种状态：

未访问（visit[i]=0）
已访问但未入栈（visit[i]=1）,
已访问并已入栈（visit[i]=2）

如果出现当先节点的子节点的状态未visit[i]=1,说明当前子节点有一条指向尚未回溯的祖先节点的边，即出现了环，无拓扑序列。

class Solution {
private:
    vector<vector<int>> edges;
    vector<int> visited;
    bool valid = true;
public:
    void dfs(int u) {
        visited[u] = 1;
        for (int v: edges[u]) {
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            }
            else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }
        visited[u] = 2;
    }
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        visited.resize(numCourses);
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
        }
        for (int i = 0; i < numCourses && valid; ++i) {
            if (!visited[i]) {
                dfs(i);
            }
        }
        return valid;
    }
};

课程表2

题目：
现在你总共有 n 门课需要选，记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。
示例 1:
输入: 2, [[1,0]]
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
算法：
（拓扑排序）广度优先 + 入度数组

class Solution
{
private:
    vector<vector<int>> graph;
    vector<int> du; 
    queue<int> work;
    vector<int> res;
    int count;
public:
    vector<int> findOrder(int numCourses, vector<vector<int>> &prerequisites)
    {
        du.resize(numCourses);
        graph.resize(numCourses);
        for (int i = 0; i < prerequisites.size(); i++)
        {
            graph[prerequisites[i][1]].push_back(prerequisites[i][0]);
            du[prerequisites[i][0]]++;
        }
        for (int i = 0; i < numCourses;i++){
            if(du[i] == 0){
                work.push(i);
            }
        }
        while(!work.empty()){
            int v = work.front();
            work.pop();
            count++;
            res.push_back(v);
            for(auto u: graph[v]){
                du[u]--;
                if(du[u] == 0){
                    work.push(u);
                }
            }
        }
        if(count != numCourses){
            res.clear();
        }
        return res;
    }
};

8.判断二部图

题目：
存在一个无向图，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。

如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为二分图。
如果图是二分图，返回 true ；否则，返回 false 。
示例 1：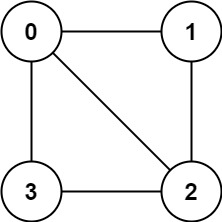
链表&图&树 - 图3

输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

class Solution {
private:
    vector<int> status;
    int valid = 1;
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        status.resize(n);
        for (int i = 0; i < n;i++){
            if(status[i] == 0){
                bool res = dfs(i,1,graph);
                if(!res)
                    return false;
            }
        }
        return true;
    }
    bool dfs(int v,int c,vector<vector<int>> graph){
        status[v] = c;
        int nextc;
        if(c==1){
            nextc = 2;
        }else{
            nextc = 1;
        }
        for (auto x: graph[v]){
            if(status[x] == 0){
                valid = dfs(x, nextc, graph);
                if(!valid)
                    return false;
            }else if(status[x] == c){
                valid = 0;
                return false;
            }
        }
        return true;
    }
};

9.二叉树

二叉树的中序遍历非递归写法

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        stack<TreeNode*> work;
        TreeNode *p = root;
        while(p||!work.empty()){
            while(p){
                work.push(p);
                p=p->left;
            }
            p = work.top();
            work.pop();
            if(--k==0){
                return p->val;
            }
            p=p->right;
        }
        return -1;
    }
};

计算完全二叉树的节点数量

算法：完全二叉树可编码，每一个节点可通过位运算得到根节点的路径。
结合二分查找，在第h层查找即可。

class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        int level = 0;
        TreeNode* node = root;
        while (node->left != nullptr) {
            level++;
            node = node->left;
        }
        int low = 1 << level, high = (1 << (level + 1)) - 1;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (exists(root, level, mid)) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return low;
    }
    //通过位运算得到节点的路径
    bool exists(TreeNode* root, int level, int k) {
        int bits = 1 << (level - 1);
        TreeNode* node = root;
        while (node != nullptr && bits > 0) {
            if (!(bits & k)) {
                node = node->left;
            } else {
                node = node->right;
            }
            bits >>= 1;
        }
        return node != nullptr;
    }
};

链表&图&树