https://towardsdatascience.com/gamma-function-intuition-derivation-and-examples-5e5f72517dee

Aerin Kim

Gamma Function — Intuition, Derivation, and Examples

Its properties, proofs & graphs

Why should I care?

Many probability distributions are defined by using the gamma function — such as Gamma distribution, Beta distribution, Dirichlet distribution, Chi-squared distribution, and Student’s t-distribution, etc. For data scientists, machine learning engineers, researchers, the Gamma function is probably one of the most widely used functions because it is employed in many distributions. These distributions are then used for Bayesian inference, stochastic processes (such as queueing models), generative statistical models (such as Latent Dirichlet Allocation), and variational inference. Therefore, if you understand the Gamma function well, you will have a better understanding of a lot of applications in which it appears!

1. Why do we need the Gamma function?

Because we want to generalize the factorial!

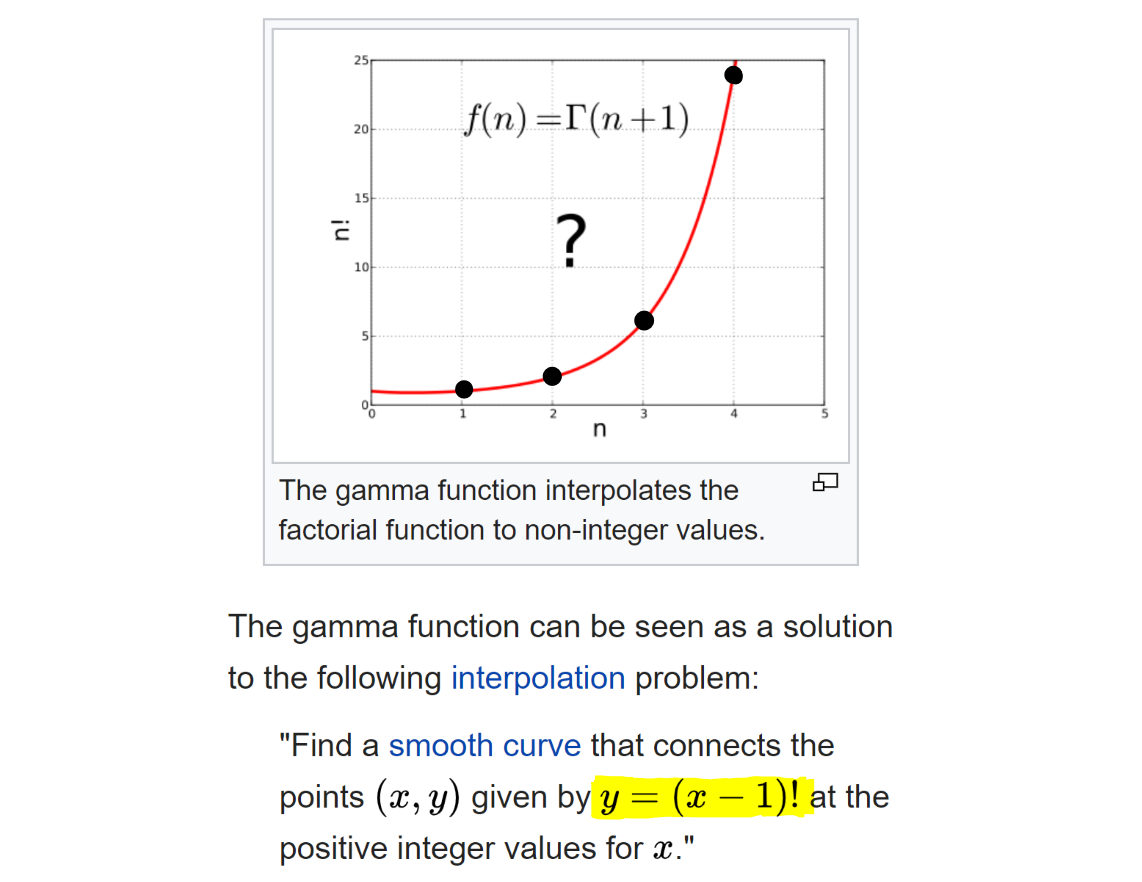
f(1) = 1, f(2) = 2!, f(3) = 3!, f(4) = 4!, … https://en.wikipedia.org/wiki/Gamma_function

The factorial function is defined only for discrete points (for positive integers — black dots in the graph above), but we wanted to connect the black dots. We want to extend the factorial function to all complex numbers. The simple formula for the factorial, x! = 1 2 … * x, cannot be used directly for fractional values because it is only valid when x is a whole number.

So mathematicians had been searching for…

“What kind of functions will connect these dots smoothly and give us factorials of all real values?”

However, they couldn’t find _finite_ combinations of sums, products, powers, exponential, or logarithms that could express x! for real numbers until…

2. Euler found the Gamma function. (In the 18th century)

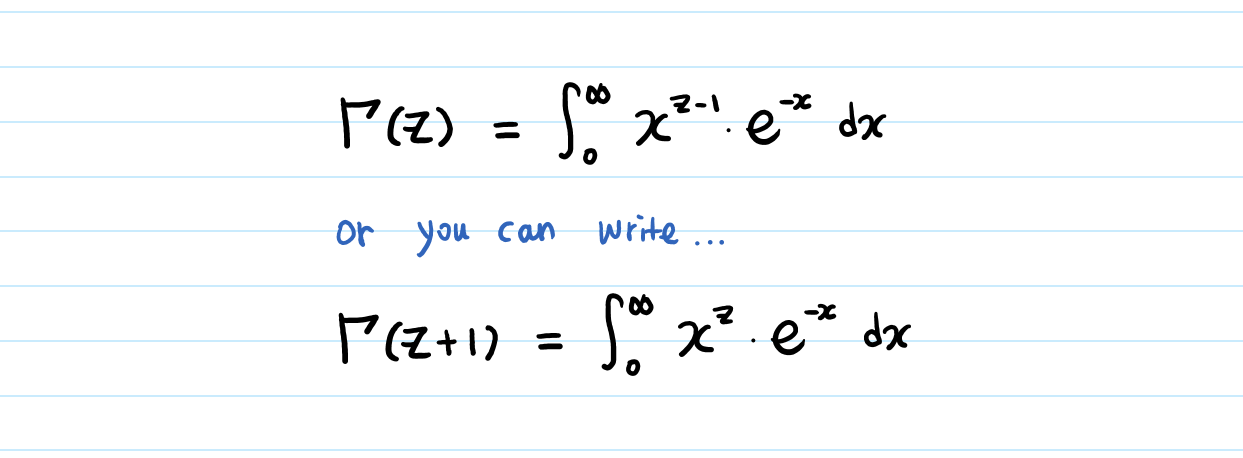
The Gamma Function: Euler integral of the second kind

The formula above is used to find the value of the Gamma function for any real value of z.

Let’s say you want to calculate Γ(4.8). How would you solve the integration above?
Can you calculate Γ(4.8) by hand? Maybe using the integral by parts?

Try it and let me know if you find an interesting way to do so! For me (and many others so far), there is no quick and easy way to evaluate the Gamma function of fractions manually. (If you are interested in solving it by hand, here is a good starting point.)

Ok, then, forget about doing it analytically. Can you implement this integral from 0 to infinity — adding the term infinite times programmatically?

You can implement this in a few ways. Two of the most often used implementations are Stirling’s approximationand Lanczos approximation.

For implementation addicts: the codes of Gamma function (mostly Lanczos approximation) in 60+ different language - C, C++, C#, python, java, etc.

Let’s calculate Γ(4.8) using a calculator that is implemented already.

We got 17.837.

17.837 falls between 3!(= Γ(4) = 6) and 4!(= Γ(5) = 24) — as we expected.

(When z is a natural number, Γ(z) =(z-1)! We are going to prove this shortly.)

Unlike the factorial, which takes only the positive integers, we can input any real/complex number into z, including negative numbers. The Gamma function connects the black dots and draws the curve nicely.

Confusion-buster: We are integrating over x (NOT z) from 0 to infinity. • x is a helper variable that is being integrated out.
• We are NOT plugging 4.8 into x. We are plugging 4.8 into z.

3. How can the Gamma function interpolate the factorial function?

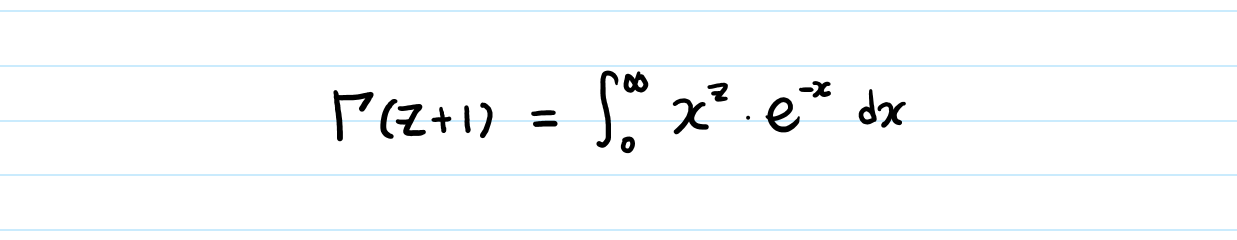
If you take a look at the Gamma function, you will notice two things.

First, it is definitely an increasing function, with respect to z.

Second, when z is a natural number, Γ(z+1) = z!
(I promise we’re going to prove this soon!)

Therefore, we can expect the Gamma function to connect the factorial.

How did the Gamma function end up with current terms x^z and e^-x?

I don’t know exactly what Euler’s thought process was, but he is the one who discovered the natural number e, so he must have experimented a lot with multiplying e with other functions to find the current form.

4. What would the graph of Gamma function look like?

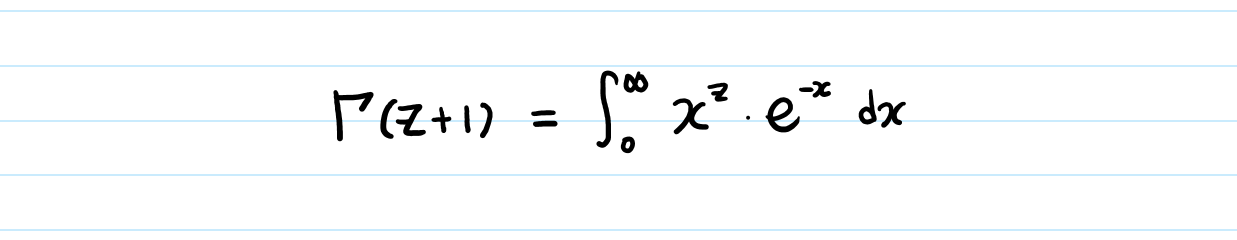
As x goes to infinity ∞, the first term (x^z) also goes to infinity ∞, but the second term (e^-x) goes to zero.

Then, will the Gamma function converge to finite values?

We can rigorously show that it converges using L’Hôpital’s rule. But we can also see its convergence in an effortless way. If you think about it, we are integrating a product of x^z — a polynomially increasing function —and e^-x — an**exponentially decreasing function. Because the value of e^-x**decreases much more quickly than that of x^z, the Gamma function is pretty likely to converge and have finite values.

Let’s plot each graph, since seeing is believing.

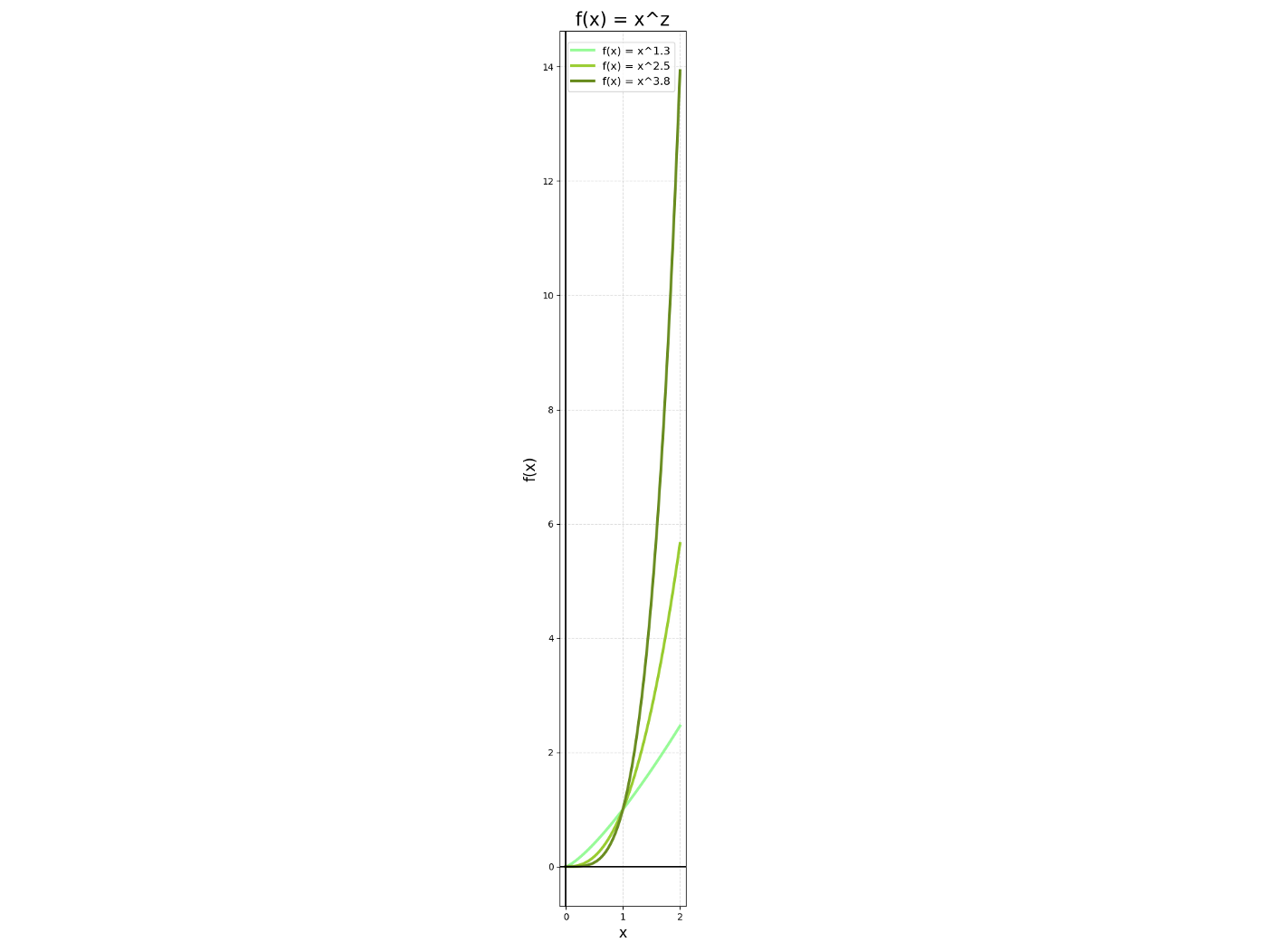
The first term x^z — polynomially increasing function.

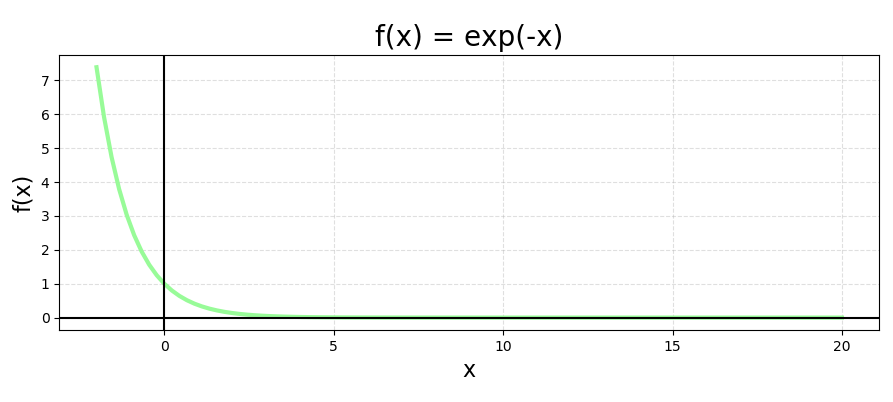
The second term e^-x — exponentially decreasing function.

The graph of x^z * e^-x

Let’s look at the case of Γ(4.8).

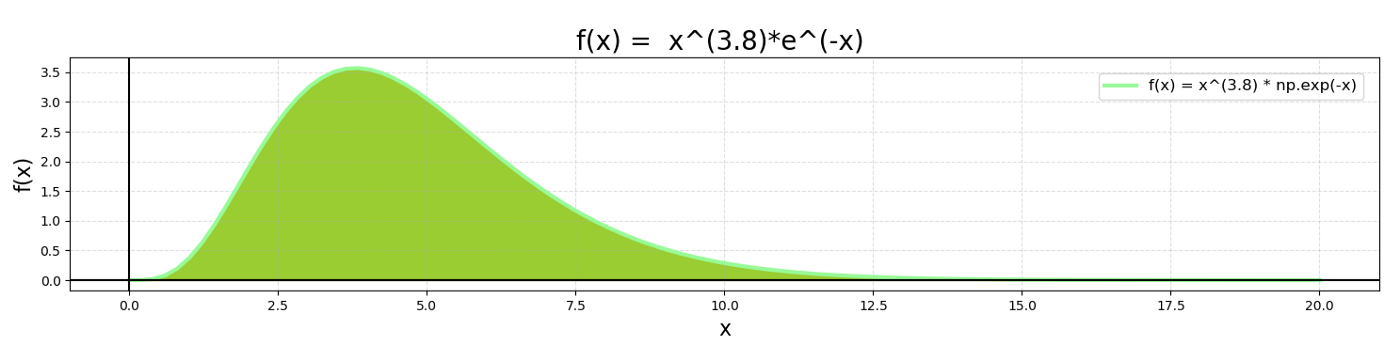
The green shaded area under the graph, denoting from 0 to infinity, is Γ(4.8) = 3.8!

Python code is used to generate the beautiful plots above. Plot it yourself and see how z changes the shape of the Gamma function!

########################
**# f(x) = exp(-x) graph #
**########################import matplotlib.pyplot as plt
import numpy as np# Create x and y
x = np.linspace(-2, 20, 100)
y = np.exp(-x)# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y, label=’f(x) = exp(-x)’, linewidth=3, color=’palegreen’)# Make the x=0, y=0 thicker
ax.set_aspect(‘equal’)
ax.grid(True, which=’both’)
ax.axhline(y=0, color=’k’)
ax.axvline(x=0, color=’k’)# Add a title
plt.title(‘f(x) = exp(-x)’, fontsize=20)# Add X and y Label
plt.xlabel(‘x’, fontsize=16)
plt.ylabel(‘f(x)’, fontsize=16)# Add a grid
plt.grid(alpha=.4, linestyle=’—‘)# Show the plot
plt.show()####################
**# f(x) = x^z graph #
**####################import matplotlib.pyplot as plt
import numpy as np# Create x and y
x = np.linspace(0, 2, 100)
y1 = x1.3
y2 = x2.5
y3 = x3.8# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y1, label=’f(x) = x^1.3’, linewidth=3, color=’palegreen’)
plt.plot(x, y2, label=’f(x) = x^2.5’, linewidth=3, color=’yellowgreen’)
plt.plot(x, y3, label=’f(x) = x^3.8’, linewidth=3, color=’olivedrab’)# Make the x=0, y=0 thicker
ax.set_aspect(‘equal’)
ax.grid(True, which=’both’)
ax.axhline(y=0, color=’k’)
ax.axvline(x=0, color=’k’)# Add a title
plt.title(‘f(x) = x^z’, fontsize=20)# Add X and y Label
plt.xlabel(‘x’, fontsize=16)
plt.ylabel(‘f(x)’, fontsize=16)# Add a grid
plt.grid(alpha=.4, linestyle=’—‘)# Add a Legend
plt.legend(bbox_to_anchor=(1, 1), loc=’best’, borderaxespad=1, fontsize=12)# Show the plot
plt.show()###############################
# f(x) = x^(3.8)*e^(-x) graph # ###############################import matplotlib.pyplot as plt
import numpy as np# Create x and y
x = np.linspace(0, 20, 100)
y = x3.8 np.exp(-x)# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y, label=’f(x) = x^(3.8) np.exp(-x)’, linewidth=3, color=’palegreen’)
ax.fill_between(x, 0, y, color=’yellowgreen’)# Make the x=0, y=0 thicker
ax.set_aspect(‘equal’)
ax.grid(True, which=’both’)
ax.axhline(y=0, color=’k’)
ax.axvline(x=0, color=’k’)# Add a title
plt.title(‘f(x) = x^(3.8)*e^(-x) ‘, fontsize=20)# Add X and y Label
plt.xlabel(‘x’, fontsize=16)
plt.ylabel(‘f(x)’ ,fontsize=16)# Add a grid
plt.grid(alpha=.4, linestyle=’—‘)# Add a Legend
plt.legend(bbox_to_anchor=(1, 1), loc=’upper right’, borderaxespad=1, fontsize=12)# Show the plot
plt.show()

The code in ipynb: https://github.com/aerinkim/TowardsDataScience/blob/master/Gamma%20Function.ipynb

5. Gamma function properties

If you take one thing away from this post, it should be this section.

Property 1.**given z > 1*Γ(z) = (z-1) Γ(z-1) or you can write it as
Γ(z+1) = z * Γ(z)

Let’s prove it using integration by parts and the definition of Gamma function.

Red Arrow: the value of e^-x decreases much more quickly than that of x^z

Beautifully proved!

Property 2. If n is a positive integerΓ(n) = (n-1)!

Let’s prove it using the property 1.

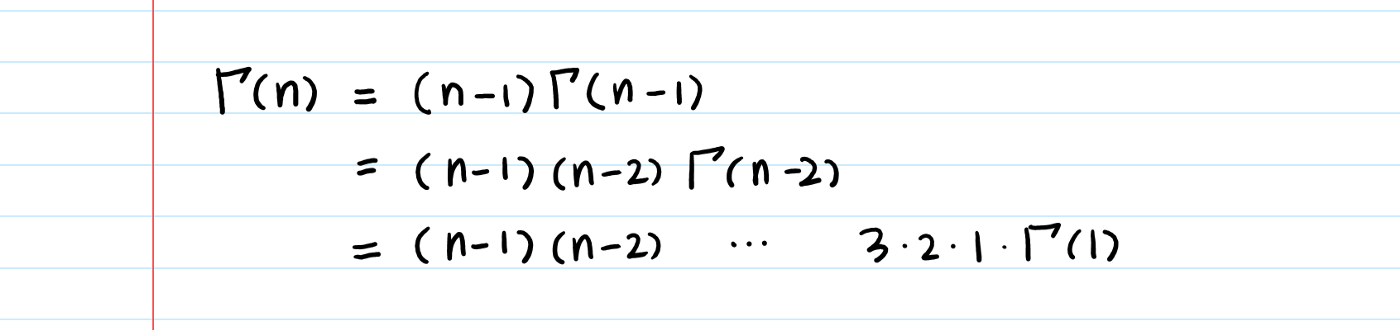
What is Γ(1)?

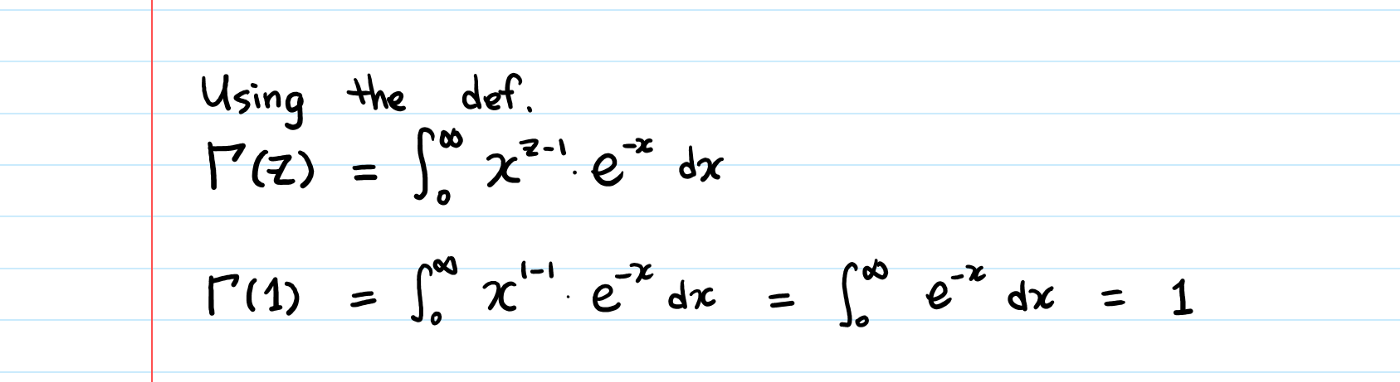
Therefore, Γ(n) = (n-1)!

You might have also seen the expression Γ(n+1) = n! instead of
Γ(n) = (n-1)!.This is just to make the right hand side n!, instead of (n-1)!
All we did was to shift n by 1.

6. Using the property of the Gamma function, show the PDF of Gamma distribution integrates to 1.

A quick recap about the Gamma “distribution” (not the Gamma “function”!): Gamma Distribution Intuition and Derivation.

Here goes the proof:

For the proof addicts: Let’s prove the red arrow above.

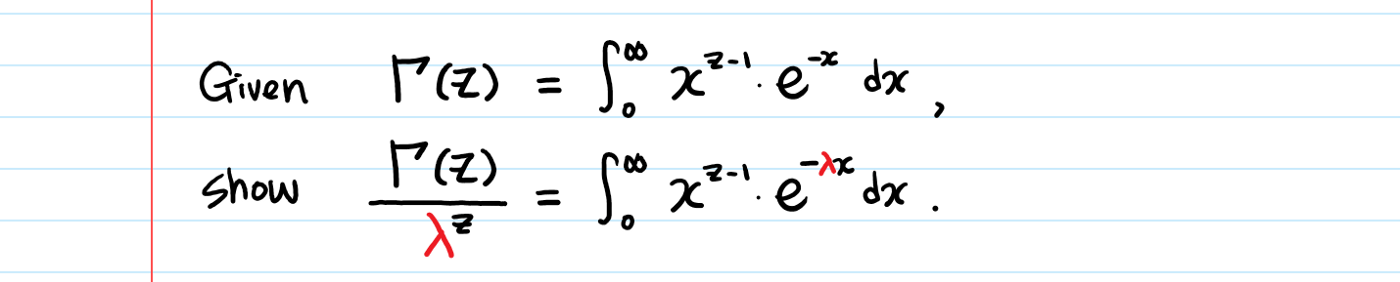
We’ll use integration by substitution.

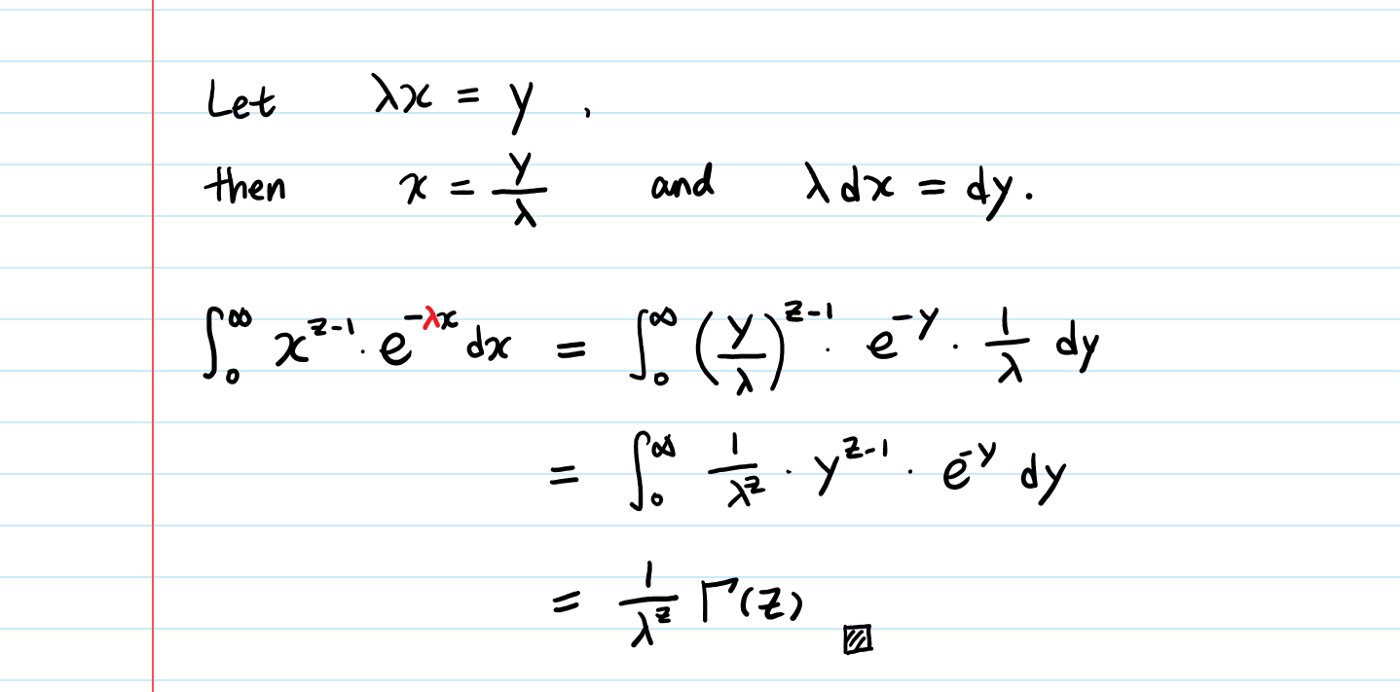
Beautifully proved again!

A few things to note:

1. How old is the Gamma function?

Pretty old. About 300 yrs. (Are you working on something today that will be used 300 years later?;)

An interesting side note: Euler became blind at age 64 however he produced almost half of his total works after losing his sight.

1. Some interesting values at points:

Γ(1/2) = sqrt(𝜋)Many interesting ways to show this:
https://math.stackexchange.com/questions/215352/why-is-gamma-left-frac12-right-sqrt-piΓ(-1/2) = -2 sqrt(𝜋)*Γ(-1) = Γ(-2) = Γ(-3) = infinity ∞**

Can you prove these?

1. Here is a quick look at the graph of the Gamma function in real numbers.

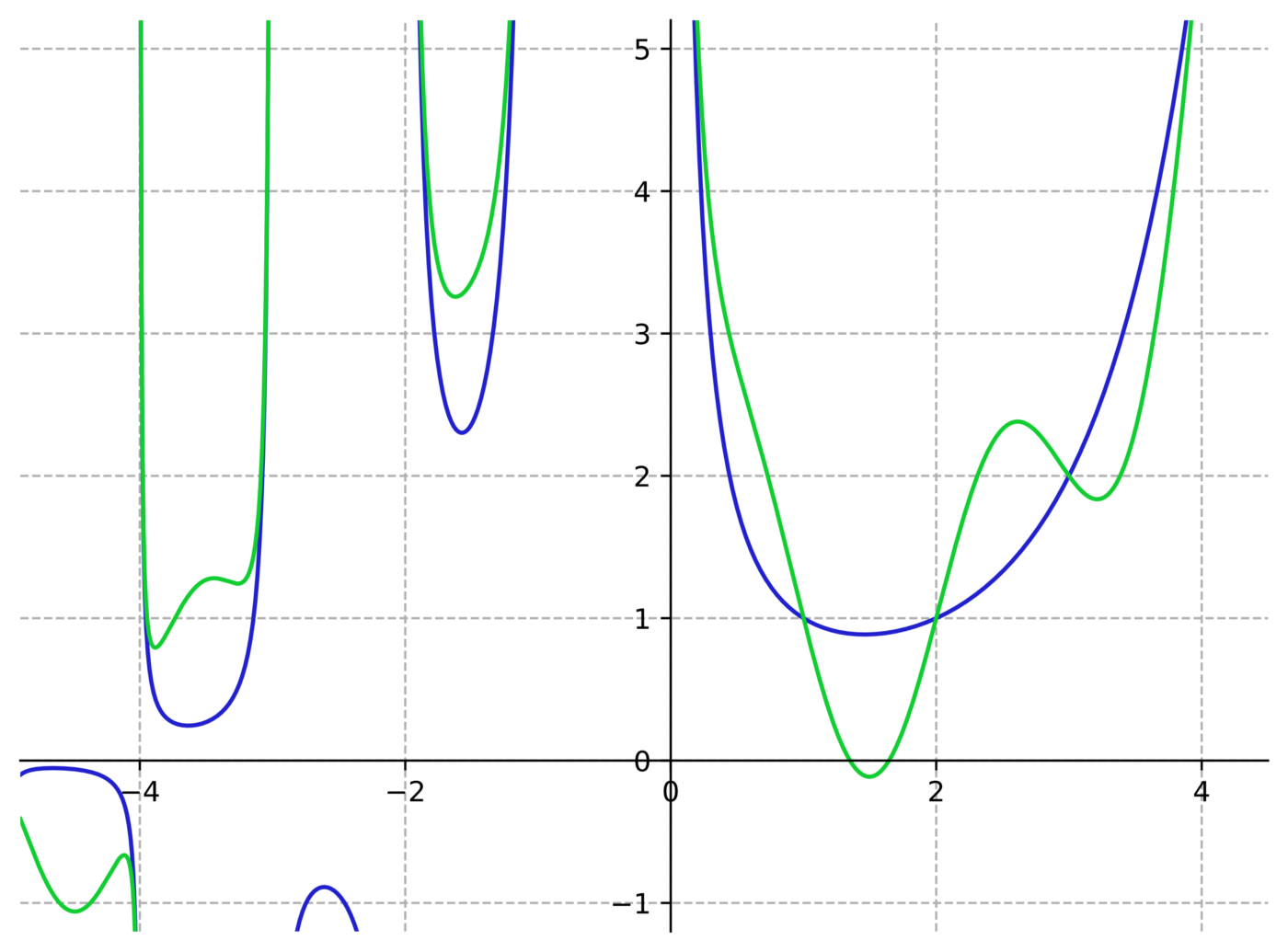
https://en.wikipedia.org/wiki/Gamma_function

The Gamma function, Γ(z) in blue, plotted along with Γ(z) + sin(πz) in green. (Notice the intersection at positive integers because sin(πz) is zero!) Both are valid analytic continuations of the factorials to the non-integers.

1. Gamma function also appears in the general formula for the volume of an n-sphere.