- 怎么学好数据结构——附动画
- 演示Data Structure Visualizations
数组
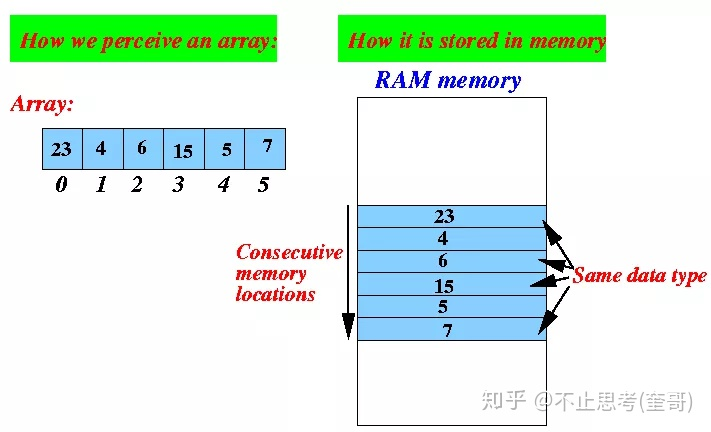
链表
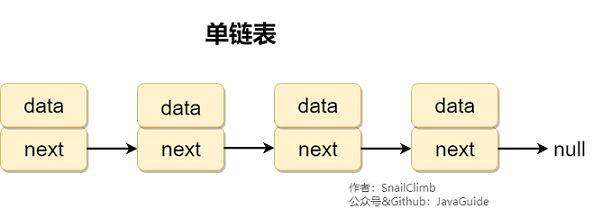
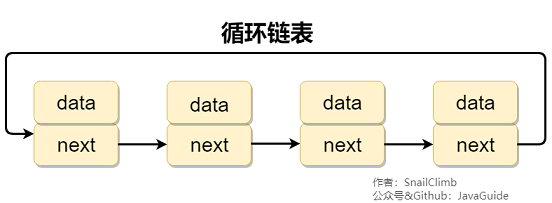
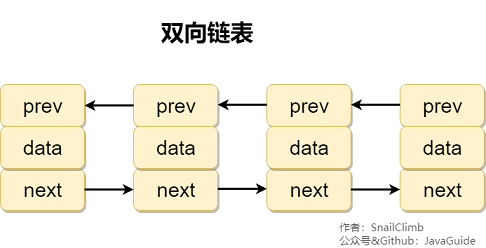
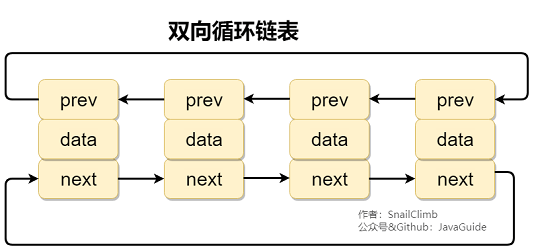
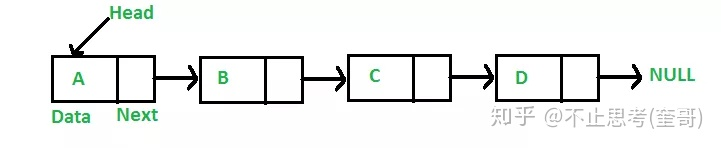
 删除
删除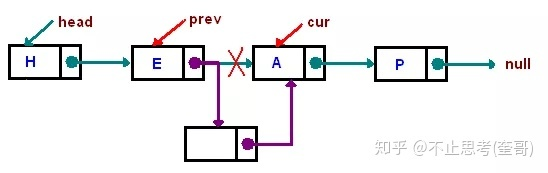 插入
插入
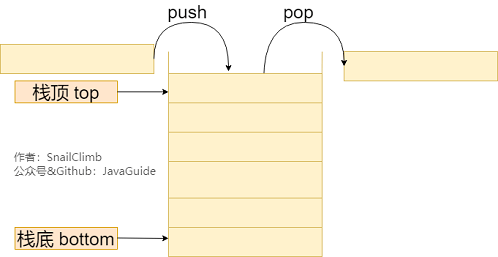
栈
实现
应用
- 浏览器前进、后退功能
- 消息队列
- 阻塞队列
- 线程池中的请求/任务队列
树
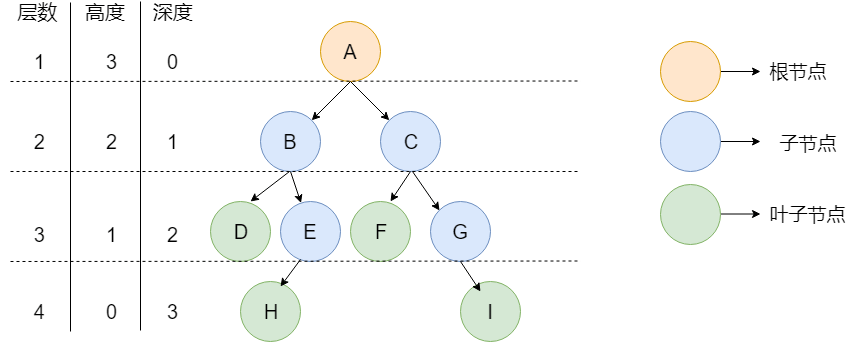
二叉树的第 i 层至多拥有 2^(i-1) 个节点,层数为 k 的二叉树至多总共有 2^k-1 个节点分类
满二叉树
每一层的结点数都达到最大值。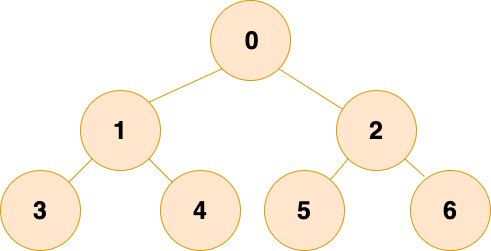
完全二叉树
完全二叉树的父结点和子节点的序号有着对应关系,利用数组存储时可以极大地节省空间,以及利用序号找到某个节点的父结点和子节点。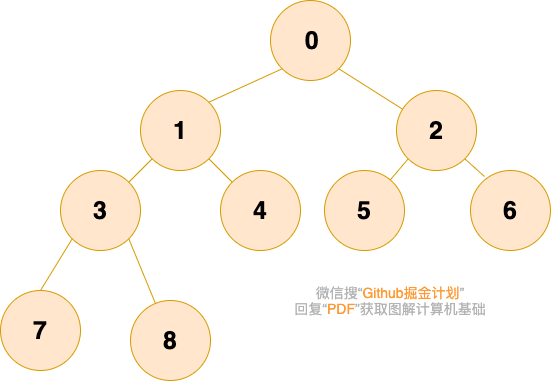
平衡二叉树
可以是空树;如果不是空树,它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。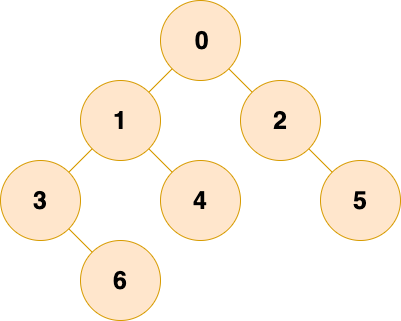
二叉查找树
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树。红黑树
复杂,暂时不用理解多深入,知道规则和变色(父节点和叔叔节点都是红色)+左旋+右旋。
漫画:什么是红黑树?
规则:
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。知乎评论:把复杂的知识用猫来表达并不能有助于理解,要从根本上”理解”红黑树,先看”2-3-4 tree”, 红黑树其实是一种”2-3-4 tree”的变形。为啥用红黑树而不用2-3-4 呢?其实是因为在C语言的数据结构上,实现2-3-4 tree比较啰嗦,使用二叉树更容易实现。谷歌搜”understand 2-3-4 tree”,你会搜到一大堆资料。
B树
B树和B+树的插入和删除 (B树删除最后一步那里有问题,最后B树和B+树的总结不一定准确)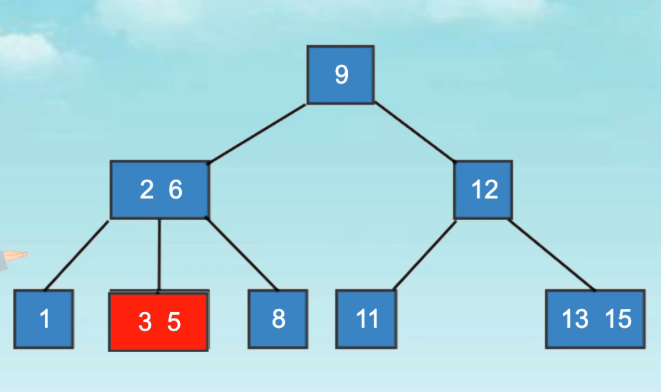
阶数3
- 根节点最少可以只有1个关键字。
- 非根节点至少有Math.floor(m/2)个关键字。
- 每个节点最多有m-1个关键字(可以存有的键值对),最多有m个叶子
- 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- 所有叶子节点都位于同一层,或者说根节点到每个叶子节点的长度都相同。
- 每个节点都存有索引和数据,也就是对应的key和value。
插入
判断当前结点key的个数是否小于等于m-1,如果满足,直接插入即可,如果不满足,将节点的中间的key将这个节点分为左右两部分,中间的节点放到父节点中即可。
删除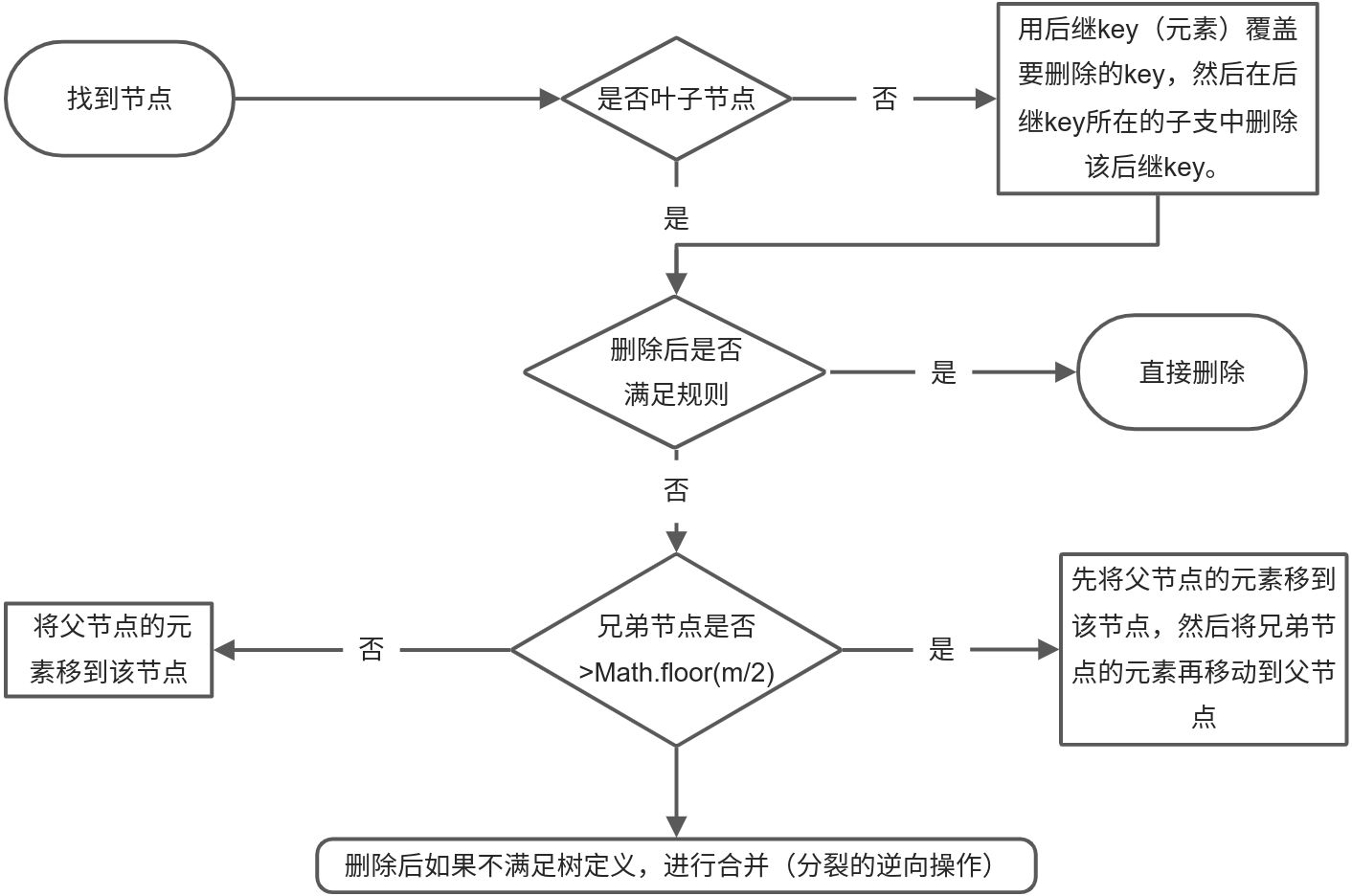
B+树
- 数据都存储在叶子节点。
- 每个叶子结点都存有相邻叶子结点的指针。
- 父节点存有右孩子的第一个元素的索引。
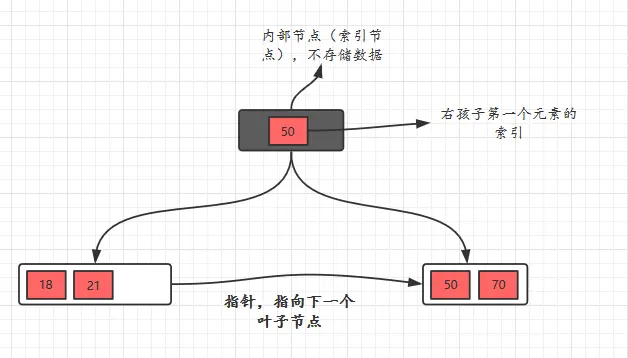
插入
当节点元素数量大于m-1的时候,按中间元素分裂成左右两部分,中间元素分裂到父节点当做索引存储,但是,本身中间元素还是分裂右边这一部分的。
删除
与B数类似,只是向兄弟节点借的时候,不移动父节点,而是更改父节点指向右孩子第一个元素的索引。
存储
- 链式存储
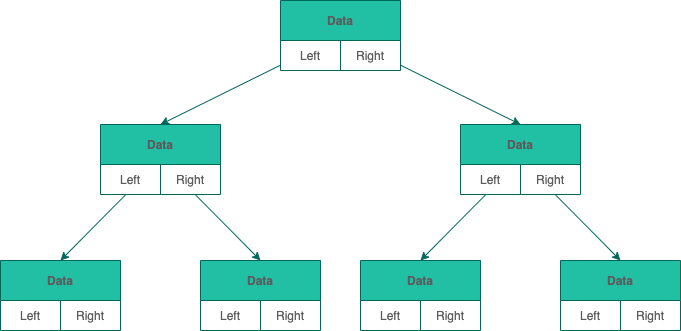
- 顺序存储
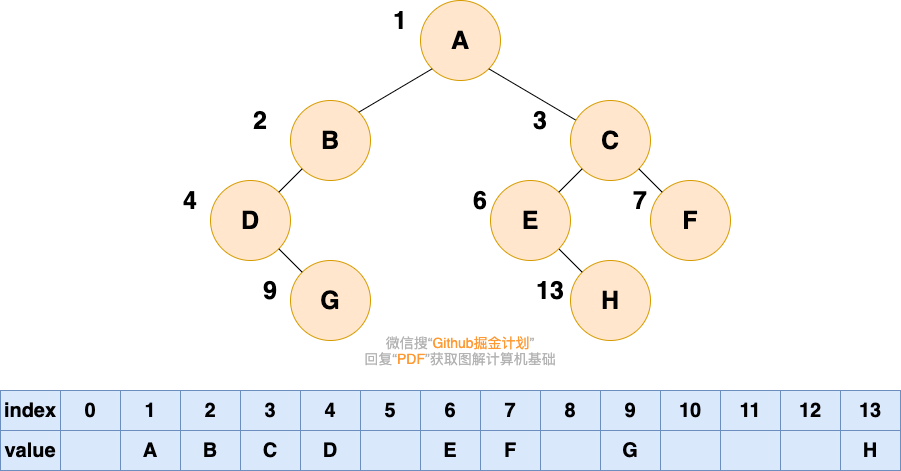
如果我们要存储的二叉树不是完全二叉树,在数组中就会出现空隙,导致内存利用率降低。
遍历
先序遍历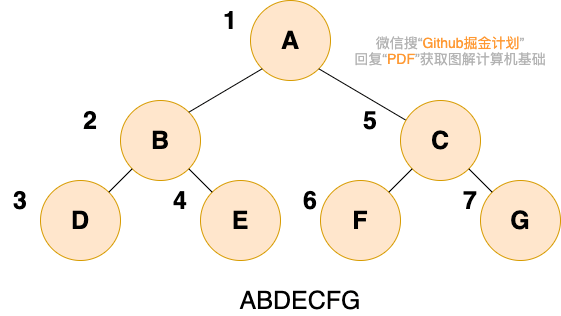
中序遍历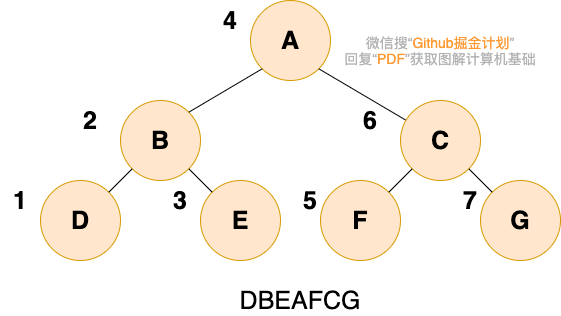
后序遍历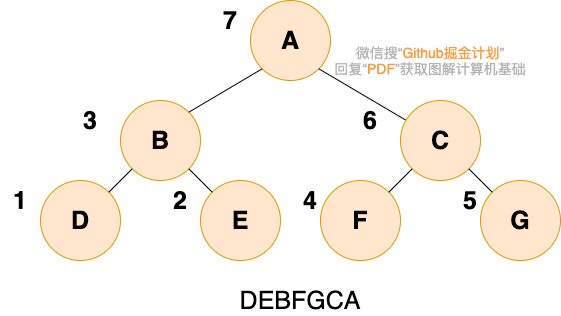
算法
斐波那契数列
复杂度
- 算法的时间与空间复杂度(一看就懂)
这段代码的时间复杂度为:O(n)for(i=1; i<=n; ++i){j = i;j++;}
T(n) = O( f(n) )
f(n) 表示每行代码执行次数之和,而 O 表示正比例关系
这段代码T(n) = (1+2n)*颗粒时间
大O符号表示法并不是用于来真实代表算法的执行时间的,它是用来表示代码执行时间的增长变化趋势的。
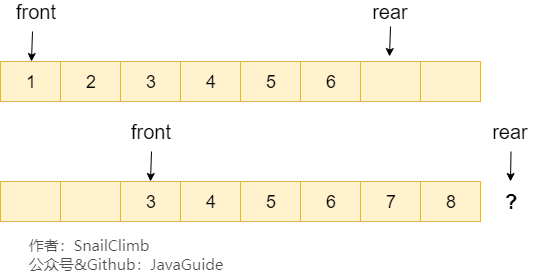 单队列
单队列 循环队列
循环队列

