Deep Factors

Deep Factors是一种global-local组合的框架预测模型，根据论文里给出的实验结果，Deep Factors的总体性能要优于现阶段主流的区间预测算法DeepAR和MQ-RNN。
优势：1.速度更快；2.学习参数少；3.global-local组合比seq2seq结构更加灵活高效。
Deep Factors一般有三种结构形式，本文复现的是第一种，即运用RNN求取sigma值。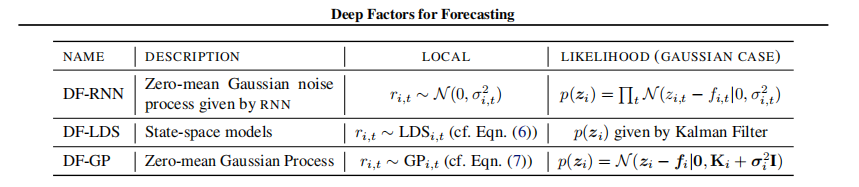

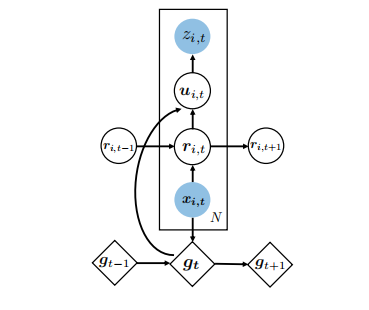
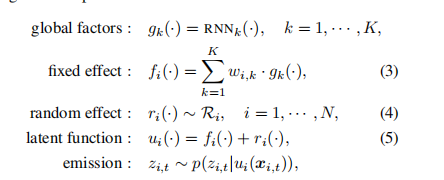
class DeepFactor(nn.Module):
    def __init__(self, input_size, global_nlayers, global_hidden_size, n_global_factors):
        super(DeepFactor, self).__init__()
        self.lstm = nn.LSTM(input_size, global_hidden_size, global_nlayers, \
                    bias=True, batch_first=True)
        self.factor = nn.Linear(global_hidden_size, n_global_factors)
    def forward(self, X):
        num_ts, num_features = X.shape
        X = X.unsqueeze(1)
        _, (h, c) = self.lstm(X)
        ht = h[-1, :, :] # num_ts, global factors
        ht = F.relu(ht)
        gt = ht
        return gt.view(num_ts, -1)
class Noise(nn.Module):
    def __init__(self, input_size, noise_nlayers, noise_hidden_size):
        super(Noise, self).__init__()
        self.lstm = nn.LSTM(input_size, noise_hidden_size, 
                noise_nlayers, bias=True, batch_first=True)
        self.affine = nn.Linear(noise_hidden_size, 1)
    def forward(self, X):
        num_ts, num_features = X.shape
        X = X.unsqueeze(1)
        _, (h, c) = self.lstm(X)
        ht = h[-1, :, :] # num_ts, global factors
        ht = F.relu(ht)
        sigma_t = self.affine(ht)
        sigma_t = torch.log(1 + torch.exp(sigma_t))
        return sigma_t.view(-1, 1)
 class DFRNN(nn.Module):
    def __init__(self, input_size, noise_nlayers, noise_hidden_size, 
            global_nlayers, global_hidden_size, n_global_factors):
        super(DFRNN, self).__init__()
        self.noise = Noise(input_size, noise_hidden_size, noise_nlayers)
        self.global_factor = DeepFactor(input_size, global_nlayers, 
                    global_hidden_size, n_global_factors)
        self.embed = nn.Linear(global_hidden_size, n_global_factors)
    def forward(self, X,):
        if isinstance(X, type(np.empty(2))):
            X = torch.from_numpy(X).float()
        num_ts, num_periods, num_features = X.size()
        mu = []
        sigma = []
        for t in range(num_periods):
            gt = self.global_factor(X[:, t, :])
            ft = self.embed(gt)
            ft = ft.sum(dim=1).view(-1, 1)
            sigma_t = self.noise(X[:, t, :])
            mu.append(ft)
            sigma.append(sigma_t)
        mu = torch.cat(mu, dim=1).view(num_ts, num_periods)
        sigma = torch.cat(sigma, dim=1).view(num_ts, num_periods) + 1e-6
        return mu, sigma